读贾志鹏《线性筛法与积性函数》笔记
1.欧拉筛法在线性时间内求素数以及欧拉函数
代码:

1 procedure get; 2 var i,j,k:longint; 3 begin 4 tot:=0; 5 fillchar(check,sizeof(check),false); 6 for i:=2 to n do 7 begin 8 if not(check[i]) then 9 begin 10 inc(tot); 11 p[tot]:=i; 12 fai[i]:=i-1; 13 end; 14 for j:=1 to tot do 15 begin 16 k:=i*p[j]; 17 if k>n then break; 18 check[k]:=true; 19 if i mod p[j]=0 then 20 begin 21 fai[k]:=fai[i]*p[j]; 22 break; 23 end 24 else 25 fai[k]:=fai[i]*(p[j]-1); 26 end; 27 end; 28 end;
其主要优越性在于:每个合数只被筛了一次,而且是被它的最小素因子筛掉的。
证明如下:
设合数n最小的质因数为p,它的另一个大于p的质因数为p′ ,令
n = pm = p′ m′ 。观察上面的程序片段,可以发现j循环到质因数p
时合数n第一次被标记(若循环到p 之前已经跳出循环,说明n 有
更小的质因数),若也被p′标记,则是在这之前(因为m′ < m)
,考虑i循环到m′ ,注意到n = pm = p′ m′ 且p, p′为不同的质数,因
此p|m′,所以当j循环到质数p后结束,不会循环到p′,这就说明不
会被p′ 筛去。
2.sigma(φ(d),d I n)=n
这也是可以证明的,这里略去(不会上传图片),其实这个结论正是noi2002 robot 1题中的关键思路
3.当n > 1时, 1 ... n中与n互质的整数和为n*φ (n) div 2
这个可以这样考虑,假如x与n互质,那么n-x也一定与n互质,所以φ(n)肯定是个偶数,将这φ(n)
两两配对,即得结论
4.若f (n) 为积性函数,则函数g n = sigma(f(d),d|n)也是积性函数,反之亦然。
莫比乌斯反演的基本形式就是:
g(n) = sigma(d|n, f(d))
f(n) = sigma(d|n, μ(n/d) * g(d))还有另外一个形式是:
g(n) = sigma(d|n, f(d))
f(n) = sigma(n|d, μ(n) * g(n/d))5.莫比乌斯函数
 |
若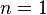 |
若 无平方数因数,且 无平方数因数,且 |
|
若 有大于 有大于 的平方数因子 的平方数因子 |
6.
莫比乌斯函数是一个积性函数。
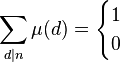 |
若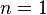 |
| 其他状况 |
以狄利克雷卷积的方法表示,则是 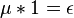 ,其中
,其中 是狄利克雷卷积的单位元,这是默比乌斯反转公式的原理。
是狄利克雷卷积的单位元,这是默比乌斯反转公式的原理。
这是可以证明的:
当n》1时,考虑n的标准分解式有k项
根据莫比乌斯函数的取值,考虑分类求左边的值,则
左边=0+1+((1-1)的k次方)-1=0
我解释一下:
(1).0是当d含有了大于1的平方数因子时,总和为0
(2).1是当d=1时,和为1
(3).这个比较巧妙,剩下的应该是莫比乌斯函数取值中的第二种情况了
实际上,(1-1)的k次方是一个组合的过程
假设我们对n的k个素因子进行选择,一共要选择k次
如果选,那么代表的它的莫比乌斯函数要变成原来的相反数,所以有个-1
如果不选,那么让它乘上个-1,保持不变
也就是说,当你把这个式子展开以后,每一项都有它的实际意义
比如(-1)*(1)*(-1)*(-1)=-1代表n有4个素因子,我进行了4次选择,选了第1,3,4个素因子,没选第二个,所以莫比乌斯函数值为-1
这样拆开的每一项除了1都代表着一个因子的莫比乌斯函数值,所以最后要减1
而我们又可以很明显的看出(1-1)的k次方=0
实际上,在robot一题中我已静经讲过这种方法的原理了
所以,命题得证
Q.E.D
7.线性时间求解莫比乌斯函数
代码:

1 procedure get; 2 var i,j,k:longint; 3 check:array[0..maxn] of boolean; 4 begin 5 fillchar(check,sizeof(check),false); 6 tot:=0;mu[1]:=1; 7 for i:=2 to maxn do 8 begin 9 if not(check[i]) then begin inc(tot);p[tot]:=i;mu[i]:=-1;end; 10 for j:=1 to tot do 11 begin 12 k:=i*p[j]; 13 if k>maxn then break; 14 check[k]:=true; 15 if i mod p[j]<>0 then mu[k]:=-mu[i] 16 else begin mu[k]:=0;break;end; 17 end; 18 end; 19 end;
实际上,莫比乌斯反演的应用有很多,证明过程也很精彩,但由于不能上传图片,我就不发上来了




