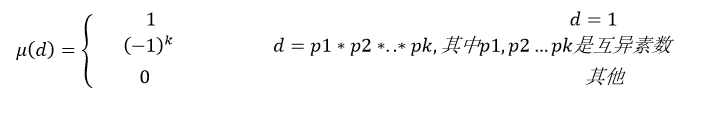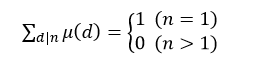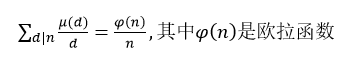欧拉函数与莫比乌斯反演

　　欧拉函数

性质：

设φ(x)表示欧拉函数，其有如下性质：

1.对素数p，φ(p)=p-1.

2.设p,q为不同的素数，φ(pq)=(p-1)(q-1).

3.欧拉函数不是完全积性函数，φ(nm)=φ(n)*φ(m)，当且仅当gcd(n,m)=1时成立

4.对于任何一个正整数的素数幂分解，N=p1^q1*p2^q2*p3^q3....pn^qn. φ(N)=N*(1-1/p1)*(1-1/p2)*(1-1/p3)....(1-1/pn)。

5.除了N=5，φ(N)都是偶数。

根据性质4，得到单个求欧拉函数算法，复杂度sqrt(n)

ll get_euler(ll n)
{
    ll res=n;
    for(ll i=2;i*i<=n;i++)
    {
        if(n%i==0) res=res/i*(i-1);
        while(n%i==0) n/=i;
    }
    if(n>1) res=res/n*(n-1);
    return res;
}

　　

线性欧拉函数打表

bool vis[maxn];
int phi[maxn];
int prime[maxn];
int cnt=0;
void getphi(int n)
{
    phi[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i])
        {
            phi[i]=i-1;
            prime[cnt++]=i;
        }
        for(int j=0;j<cnt&&prime[j]*i<=n;j++)
        {
            int x=prime[j];
            vis[i*x]=true;
            if(i%x==0)
            {
                phi[i*x]=phi[i]*x;
                break;
            } else
            {
                phi[i*x]=phi[i]*phi[x];
            }
        }
    }
}

　　莫比乌斯反演

设F(n),f(n)是定义在非负整数集合的两个函数，且满足$F(n)=\sum_{d|n} f(d)$

 

莫比乌斯反演的形式：

另一种描述是：

一种是和所有的约数有关一种是和所有的倍数有关，解题的时候要根据题目选择合适的表达形式，感觉第二种用的比较多。

关于莫比乌斯函数mu，他的定义如下：

这个莫比乌斯函数有一些性质：

（1）

（2）

莫比乌斯函数打表：

ll prime[maxn],mob[maxn],cnt=0;
bool vis[maxn]={0};
void Mobius()
{
    mob[1]=1;
    cnt=0;
    vis[1]=true;
    for(ll i=2;i<maxn;i++)
    {
        if(!vis[i])
        {
            prime[cnt++]=i;
            mob[i]=-1;
        }
        for(ll j=0;j<cnt&&prime[j]*i<maxn;j++)
        {
            vis[i*prime[j]]=true;
            if(i%prime[j])
            {
                mob[i*prime[j]]=-mob[i];
            }
            else
            {
                mob[i*prime[j]]=0;
                break;
            }
        }
    }
}