洛谷3371 spfa模板题

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

 

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

 

输出格式：

 

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

 

输入输出样例

输入样例#1： 复制

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1： 复制

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

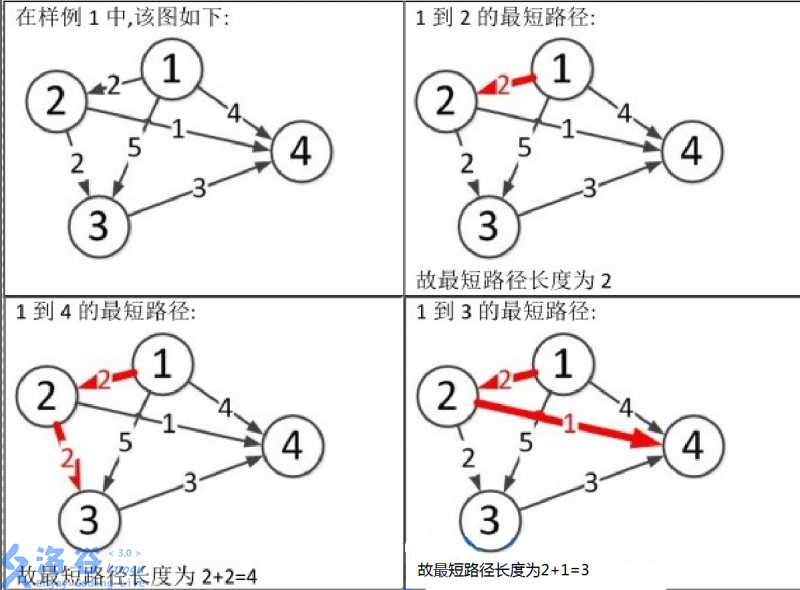
样例说明：

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int inf=2147483647;
const int  maxn=10005;
const int maxm=500005;
int n,m,s,cnt=0;
int dist[maxn],vis[maxn],head[maxm];
struct st
{
    int u,v,w;
    int next;
}edge[maxm];
void add(int u,int v,int w)
{
    edge[cnt].u=u;
    edge[cnt].v=v;
    edge[cnt].w=w;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
void spfa()
{   int i;
    queue<int> q;
    for(i=1;i<=n;i++)
    {
        dist[i]=inf;
        vis[i]=0;
    }
    q.push(s);
    dist[s]=0;
    vis[s]=1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        vis[u]=0;
        for(int i=head[u];i!=-1;i=edge[i].next)
        {
            int v=edge[i].v;
            if(dist[v]>dist[u]+edge[i].w)
            {
                dist[v]=dist[u]+edge[i].w;
                if(vis[v]==0)
                {
                    vis[v]=1;
                    q.push(v);
                }
            }
        }
    }
}
int main()
{
    int i;
    scanf("%d%d%d",&n,&m,&s);
    memset(head,-1,sizeof(head));
    for(i=0;i<m;i++)
    {   int x,y,w;
        scanf("%d%d%d",&x,&y,&w);
        add(x,y,w);
    }
    spfa();
    int flag=0;
    for(i=1;i<=n;i++)
    {   if(i!=1) printf(" ");
        if(s==i) printf("0");
        else
        {
            printf("%d",dist[i]);
        }
    }
    return 0;
}