CCPC-Wannafly Winter Camp Day3 小清新数论(莫比乌斯反演反演加杜教筛)

题目描述

 

这是一道比较基础的数论题。

给出一个整数 n，计算。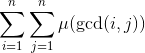 

输入描述

 

输入一行包含一个整数 n(1 \leq n \leq 10^{10})n(1≤n≤1010)。

 

输出描述

 

输出一行一个整数，表示答案。答案可能很大，请对 998244353998244353 取模后输出。

 

样例输入 1 

5

样例输出 1

14

样例输入 2 

100

样例输出 2

3631

枚举d，则原式为：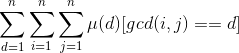

把d提出来：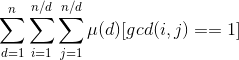

即：

然后后面那个式子就套莫比乌斯反演:设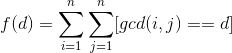

注意此n非彼n，下面的n都代表原本的n/d,原来的n用N表示。

设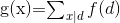 

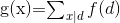
则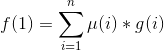

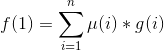
g(x）是个什么玩意

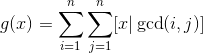
把x提出来

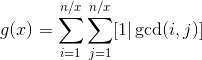
显然1|gcd(i,j)永远成立，即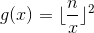

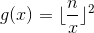
带回去：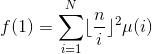

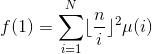
把n换回去

然后又是经典套路。

设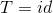

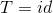
则

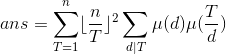
前面可以分块搞。

后面，可以观察到是两个莫比乌斯函数相卷积

上杜教筛。

设,为其前缀和。

设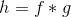

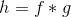
拿出杜教筛的式子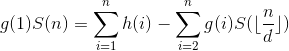

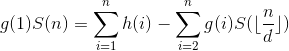
问题来了，拿什么做g?

答案：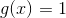

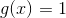
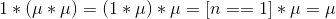
即

然后就是杜教筛搞了。

#include <bits/stdc++.h>
#define maxn 10000005
using namespace std;
typedef long long ll;
ll prime[maxn/10],phi[maxn];
ll mob[maxn],T[maxn],sum[maxn];
bool vis[maxn];
int cnt;
const ll mod=998244353;
unordered_map<ll,ll> dmu,dT;
void init()
{
    mob[1]=phi[1]=T[1]=1;
    for(int i=2;i<maxn;++i)
    {
        if(!vis[i])
        {
            prime[cnt++]=i;
            T[i]=-2;
            mob[i]=-1;
        }
        for(int j=0;j<cnt&&prime[j]*i<maxn;++j)
        {
            vis[i*prime[j]]=true;
            if(i%prime[j])
            {
                mob[i*prime[j]]=-mob[i];
                T[i*prime[j]]=T[i]*T[prime[j]];
            }
            else
            {
                if((i/prime[j])%prime[j])
                {
                    T[i*prime[j]]=T[i/prime[j]];
                }
                break;
            }
        }
    }
    for(ll i=1;i<maxn;++i)
    {
        sum[i]=(sum[i-1]+mob[i]+mod)%mod;
    }
    for(ll i=1;i<maxn;++i)
    {
        T[i]=(T[i-1]+T[i]+mod)%mod;
    }
}
ll djmu(ll n)
{
    ll res=1;
    if(n<maxn) return sum[n];
    else if(dmu.count(n)) return dmu[n];
    ll tmp;
    for(ll i=2;i<=n;i=tmp+1)
    {
        tmp=n/(n/i);
        res-=djmu(n/i)*(tmp-i+1)%mod;
    }
    res=(res%mod+mod)%mod;
    return dmu[n]=res;
}
ll djT(ll n)
{
    if(n<maxn) return T[n];
    if(dT.count(n)) return dT[n];
    ll res=djmu(n),tmp;
    for(ll i=2;i<=n;i=tmp+1)
    {
        tmp=n/(n/i);
        res=(res-(tmp-i+1)*djT(n/i)%mod+mod)%mod;
    }
    res=(res+mod)%mod;
    return dT[n]=res;
}
int main()
{
    ll n,tmp,res=0;
    init();
    cin>>n;
    //cout<<djT(1e9)<<" "<<djmu(1e9)<<endl;
    for(ll i=1;i<=n;i=tmp+1)
    {
        tmp=n/(n/i);
        ll temp=(n/i)%mod;
        temp=temp*temp%mod;
        temp=(djT(tmp)-djT(i-1)+mod)%mod*temp%mod;
        res=(res+temp)%mod;
    }
    cout<<res<<endl;
    return 0;
}