杜教筛

杜教筛能在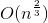内求出一个积性函数的前缀和。

比如要求前缀和。其中f(i)是一个积性函数，那么我们需要另找一个积性函数g(i)，设h(i)为f与g的狄利克雷卷积,S(i)为f(i)的前缀和，则有公式如下：

 

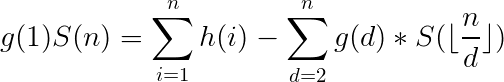
也就是说，我们找到合适的函数g,使函数h的前缀和能很快算出来，那么我们就能求出S（n）

上一个洛谷模板题：

https://www.luogu.org/problemnew/solution/P4213

#include <bits/stdc++.h>
#define maxn 5000005
using namespace std;
typedef long long ll;
ll prime[maxn/10],phi[maxn];
int mob[maxn];
bool vis[maxn];
int cnt;
void init()
{
    mob[1]=phi[1]=1;
    for(int i=2;i<maxn;++i)
    {
        if(!vis[i])
        {
            prime[cnt++]=i;
            mob[i]=-1;
            phi[i]=i-1;
        }
        for(int j=0;j<cnt&&prime[j]*i<maxn;++j)
        {
            vis[i*prime[j]]=true;
            if(i%prime[j])
            {
                mob[i*prime[j]]=-mob[i];
                phi[i*prime[j]]=phi[i]*phi[prime[j]];
            }
            else
            {
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
        }
    }
    for(int i=1;i<maxn;++i)
    {
        mob[i]=mob[i-1]+mob[i];
        phi[i]=phi[i-1]+phi[i];
    }
}
unordered_map<ll,ll> dphi;
unordered_map<int,int> dmu;
int djmu(int n)
{
    if(n<=5000000) return mob[n];
    else if(dmu.count(n)) return dmu[n];
    int tmp,res=0;
    for(int i=2;i<=n;i=tmp+1)
    {
        tmp=n/(n/i);
        res+=(tmp-i+1)*djmu(n/i);
    }
    res=1-res;
    return dmu[n]=res;
}
ll djphi(ll n)
{
    if(n<=5000000) return phi[n];
    else if(dphi.count(n)) return dphi[n];
    ll tmp,res=0;
    for(ll i=2;i<=n;i=tmp+1)
    {
        tmp=n/(n/i);
        res+=(tmp-i+1)*djphi(n/i);
    }
    res=n*(n+1)/2-res;
    return dphi[n]=res;
}
int main()
{
    int t;
    init();
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        printf("%lld %d\n",djphi(n),djmu(n));
    }
    return 0;
}