李宏毅机器学习2022年学习笔记(二)-- Tips for Training
一、 General Guide——如何达到更好的效果
1. Training data 出现的问题训练完一次模型后,根据训练集的损失以及测试集的损失来确定网络需要进行模型改进还是优化函数改进。
整体调整方向如下图所示:
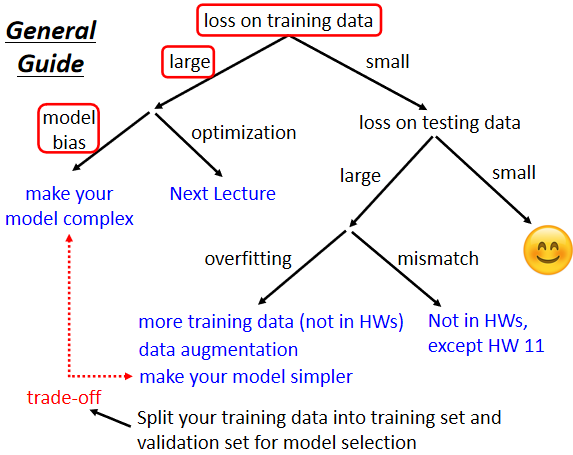
如果你觉得模型预测的结果不满意的话,第一件事情你要做的事情是,检查你的training data的loss,看看你的model在training data上面有没有学起来,再去看testing的结果。如果你发现你的training data的loss很大,显然它在训练集上面也没有训练好。有两个可能的原因,第一个可能是Model Bias(模型偏差),第二个是Optimization Issue(优化问题)
① Model Bias(模型偏差)
原因:适用的模型太简单,不足以让 loss 足够低(太简单的模型没法精确描述复杂的问题)
在选用的模型组成的 function set (函数集)中没有一个最优的 function 可以让 Loss 足够低。
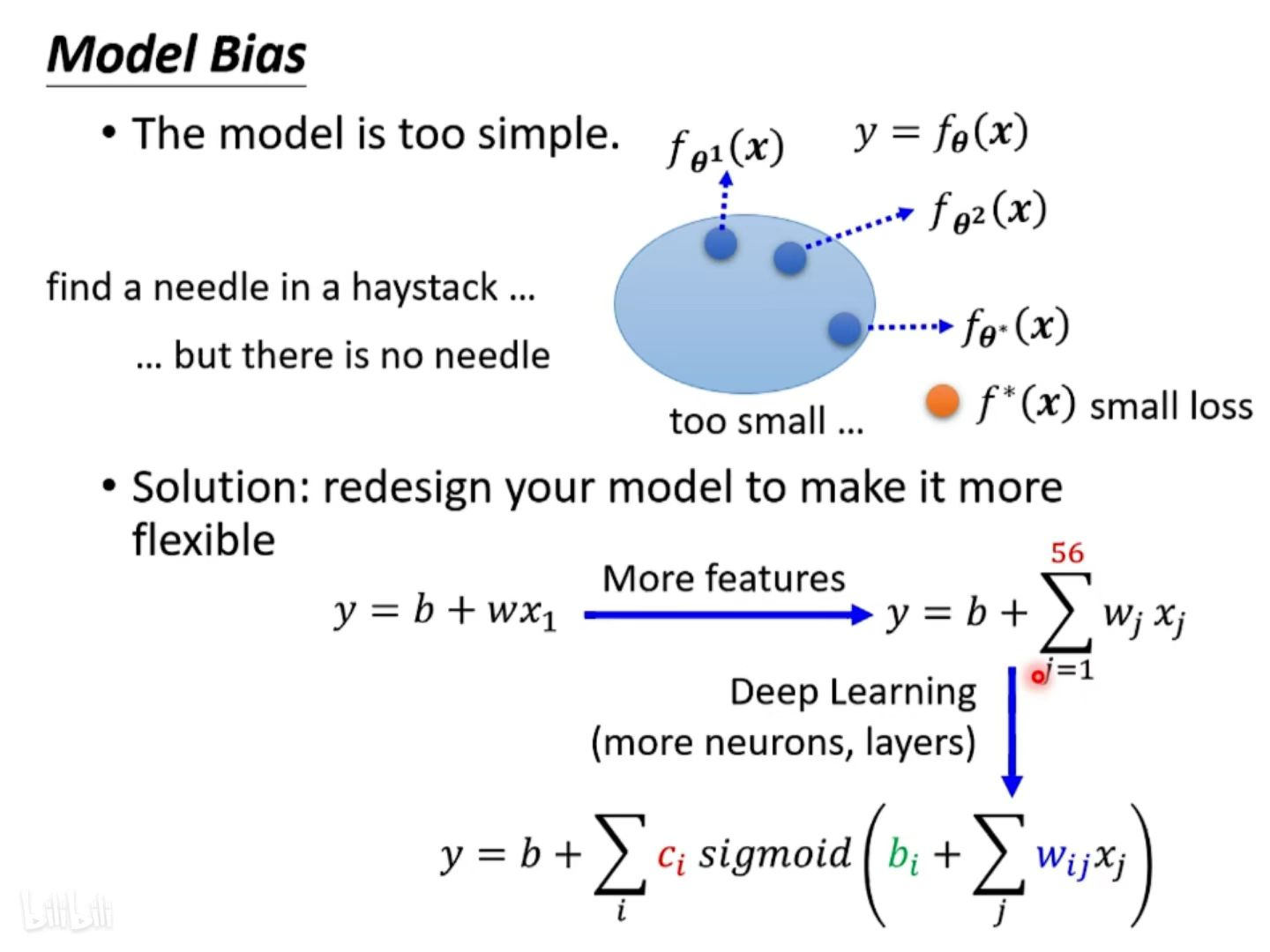
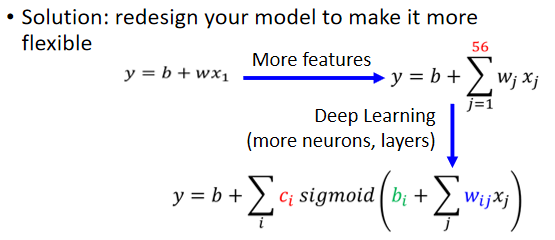
解决方案:调整模型,让模型变复杂变得有弹性,使模型能够包含更多情况。
使模型变复杂的方法:
1、使用更多的特征作为自变量。
2、加深神经网络,用到更多的神经元和层数。
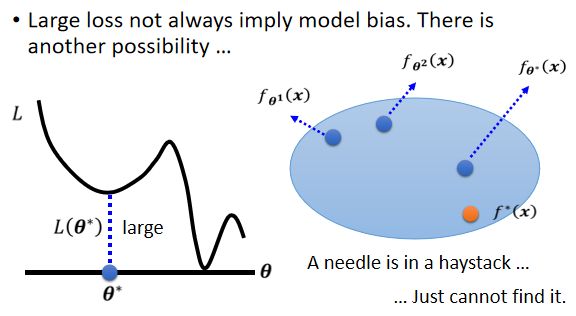
② Optimization Issue
原因:在利用Gradient descent寻找最优解时,可能会陷入局部最优解(local minima)
gradient descent方法,没办法帮我们找出 loss 低的 function,gradient descent 是解一个 optimization 的问题,找到 θ* 然后就结束了。但是 loss 不够低。这个 model 组成的 function set 里面,存在某一个 function,它计算出的 loss 是足够低的,但是 gradient descent 找不到这一个 function。
如何区分上述两种情况?
-
遇到某一任务目标可以先跑一些比较小、比较浅的 network,或甚至用一些不是 deep learning 的方法(比较容易做Optimize的,避免出现优化失败的情况)
-
如果发现在这基础上增加复杂度后的层数深的 model 跟浅的 model 比起来,深的model明明弹性更大更复杂,但 Loss 却没有办法比浅的model压得更低,那就代表 optimization 有问题
2. Testing data 出现的问题
假设在 training data 的loss变小了之后,接下来可以来看 testing data loss,如果testing data loss也小,比strong baseline还要小,那训练就结束了。
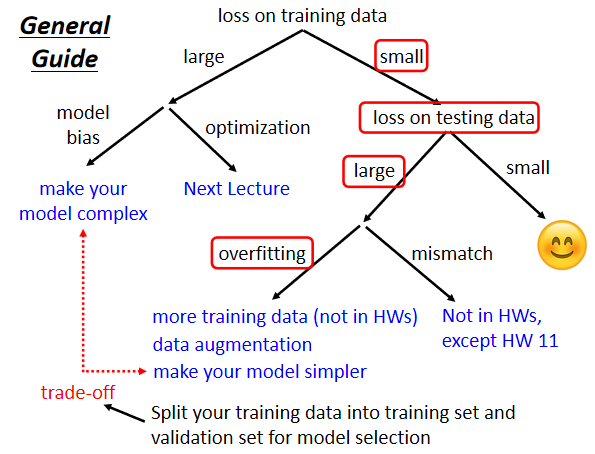
但是如果training data上面的loss小,testing data上的loss大,那可能就是真的遇到 overfitting 的问题。
Overfitting
表现形式:training的loss小,testing的loss大。
极端情况进行解释原因:训练出的模型只是记住了训练集中的输入和输出的对应关系,对于未知的部分输出是一个随机的,这种情况下在训练集中的损失为0,测试集中的损失极高。
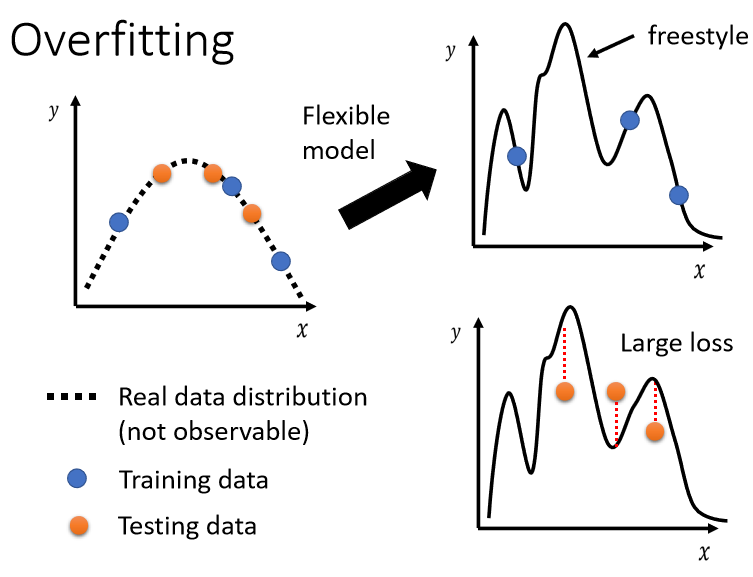
解决方式:
1. 增加训练集:可以使用data augmentation的方式进行数据扩充,例如图像中的旋转、放缩等操作(上下颠倒的操作很有可能会造成数据在真实世界中的无意义,所以很少用,要根据你对资料的特性,对你现在要处理的问题的理解来选择合适的data augmentation的方式)。

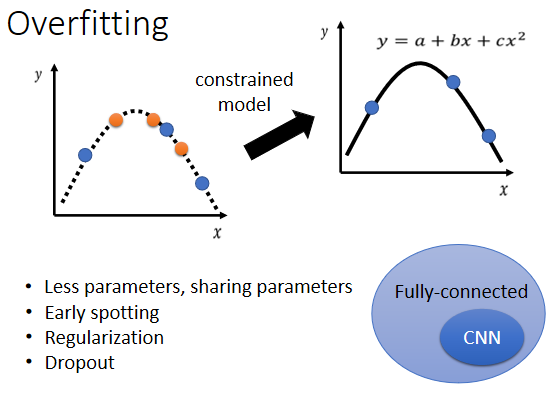
2. 限制模型的弹性:
1)给较少的参数:如果是deep learning的话,就给它比较少的神经元的数目。本来每层一千个神经元,改成一百个神经元之类的;或者是你可以让 model 共享参数,让一些参数有一样的数值。
P.S. fully-connected network(全连接网络)是一个比较有弹性的架构;而CNN(卷积神经网络)是一个比较有限制的架构,它是针对影像的特性,来限制模型的弹性。
所以 fully-connected network 可以找出来的function所形成的集合,是比较大的;CNN 的 model 所找出来的 function,它形成的 function set 是比较小的,实际上都包含在fully-connected的network里面。但是就是因为CNN有比较大的限制,所以CNN在影像上反而会做得比较好。
2)使用较少的features
3)Early stopping:训练设置提前结束的条件。(另还有Regularization正则化的方式)
4)Dropout:将部分神经元进行禁用。
二、Bias-Complexity Trade-off——模型偏置与弹性
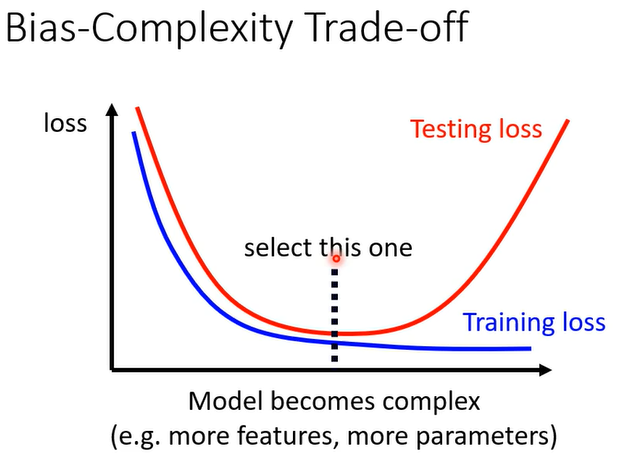
所谓比较复杂就是,它可以包含的function比较多,它的参数比较多,这个就是一个比较复杂的 model
随著model越来越复杂,Training 的 loss 可以越来越低,
当model越来越复杂的时候,刚开始,testing 的 loss 会跟著下降;但是当复杂的程度,超过某一个程度以后,Testing的loss就会突然暴增了
原因:
model 越来越复杂的时候,复杂到某一个程度,overfitting 的状况就会出现,所以在 training 的 loss 上面,可以得到比较好的结果;
但是在 Testing 的 loss 上面,会得到比较大的loss
因此我们需要设计一个 model ,既不是太复杂的,也不是太简单的,这个 model 刚好可以在训练集上给我们最好的结果(给我们最低的 loss)
① 如何选出有较低testing-loss的模型?⇒ Cross Validation(交叉验证)
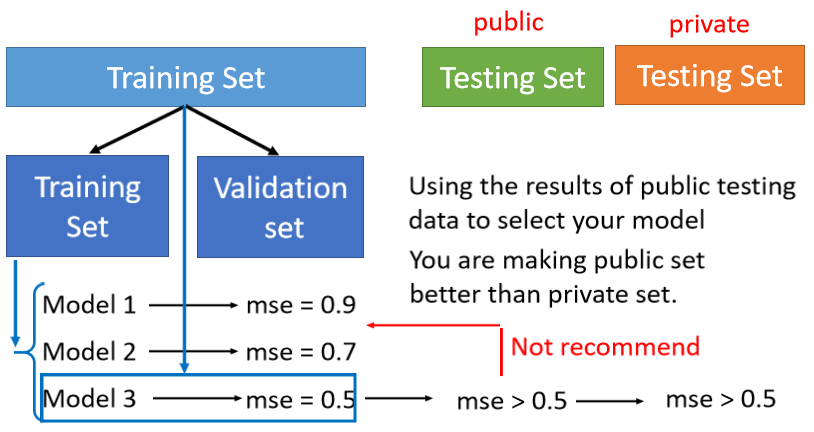
方法:把Training的资料分成两半,一部分叫作 Training Set(训练集),一部分是Validation Set(验证集)
在这组数据里,有90%的资料放在 Training Set 里面,有10%的资料会被拿来做Validation Set。
在Training Set上训练出来的模型拿到 Validation Set 上面,衡量它们的 Loss 值,根据 Validation Set 计算出的数值从而挑选选用哪个模型,不要管在public testing set上的结果,避免overfiting
② 如何合理的分 training set 和 validation set —— N-fold Cross Validation(N-重交叉验证)
N-fold Cross Validation 具体步骤如下:
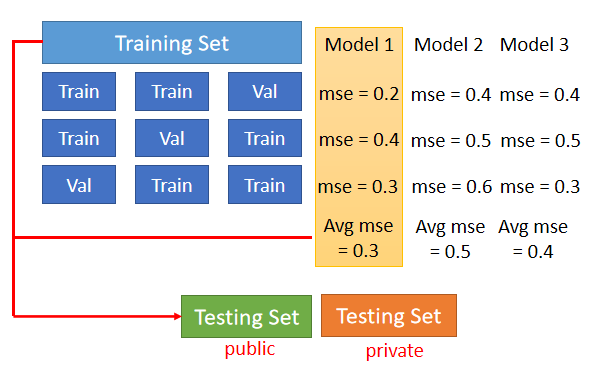
1. 先把训练集切成 N 等份,在上图例子里我们切成三等份。切完以后,拿其中一份当作 Validation Set,另外两份当 Training Set,然后要重复三次
2. 将组合后的三个 model,相同环境下,在 Training data set 和 Validation data set 上面通通跑一次。然后把这每个 model 在这三类数据集的结果都平均起来,看看哪个 model 计算出的结果最好
如果你用这三个fold(层)得出来的结果是 model 1 最好,便把 model 1 用在它所划分的两组 Training Set 上,然后训练出来的模型再用在 Testing Set 上面
③ MisMatch —— 训练集跟测试集的分布是不一样的
在训练模型的过程,也可能会出现另一种形式的问题,称为mismatch。
mismatch产生的原因与overfitting不一样。一般的overfitting你可以用增加更多的数据集来克服,但是mismatch是指训练集跟测试集它们的分布是不一样的。即使再增加数据集也没有用,例如:training data set 和 test data set 选取了来源不同的数据集,用于成像、图像增强等的操作均不同,这样的实验是没有意义的。
三、Critical Point(临界点)
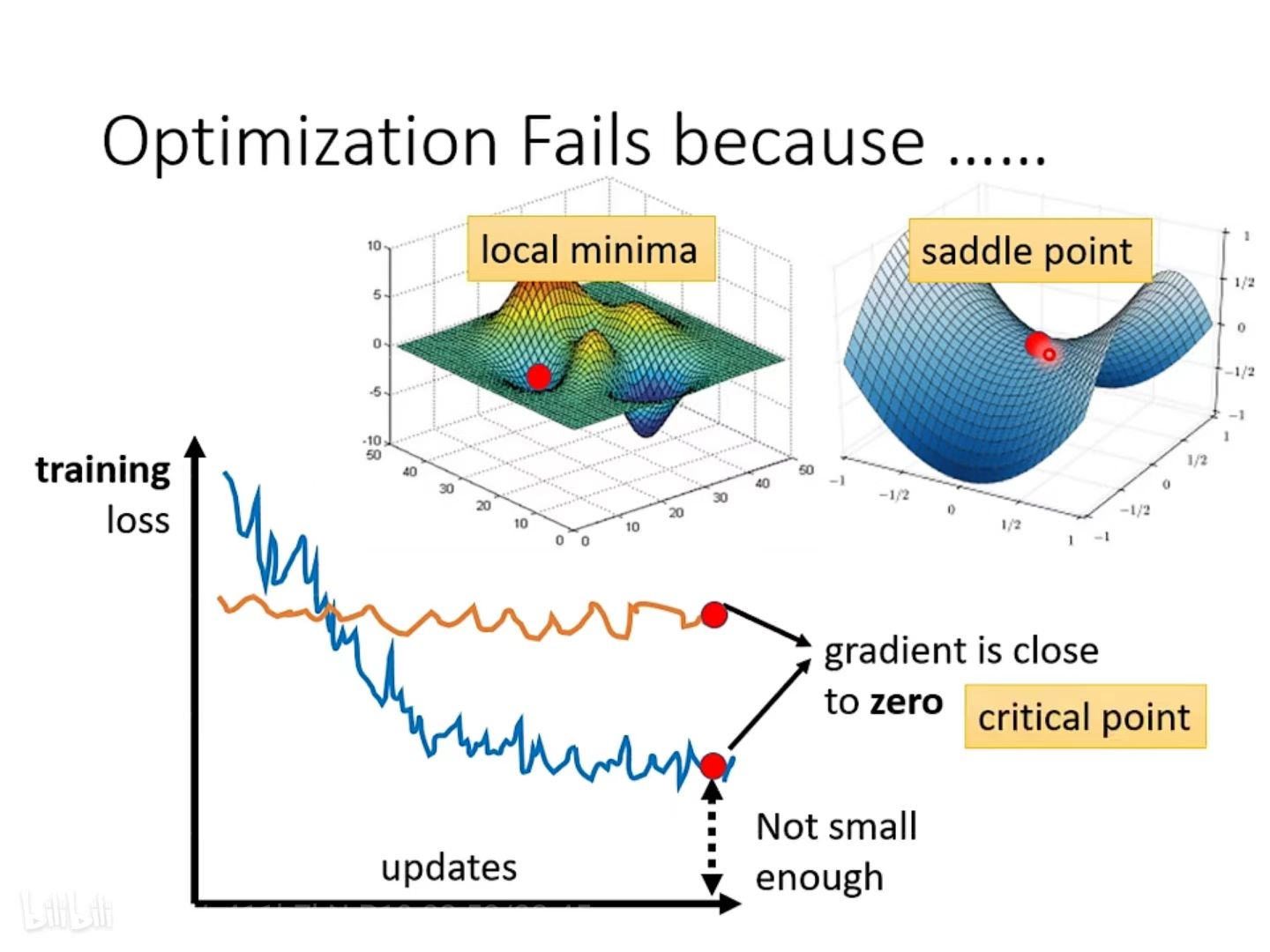
如果训练过程中经过很多个epoch后,loss还是不下降,那么可能是因为梯度(斜率)接近于 0,导致参数更新的步伐接近于0,所以参数无法进一步更新, loss也就降不下去。
梯度接近于 0 的位置就叫做临界点。而临界点中的saddle point(鞍点)还能找到办法让loss降低,就是改变一下梯度下降的方向
local minima(局部极小值):如果是卡在local minima,那可能就没有路可以走了
saddle point(鞍点):这个点在某一方向是最低点,但是在另一侧可能是最高点,卡在saddle point的话,saddle point旁边还是有路可以走的
global minima(全局最小值):已经达成目标
1. 如何判断临界点的类型 ⇒ 考察 θ 附近Loss的梯度 → 泰勒展开 → 海塞矩阵H
泰勒展开式 Tayler Series Approximation,其中,
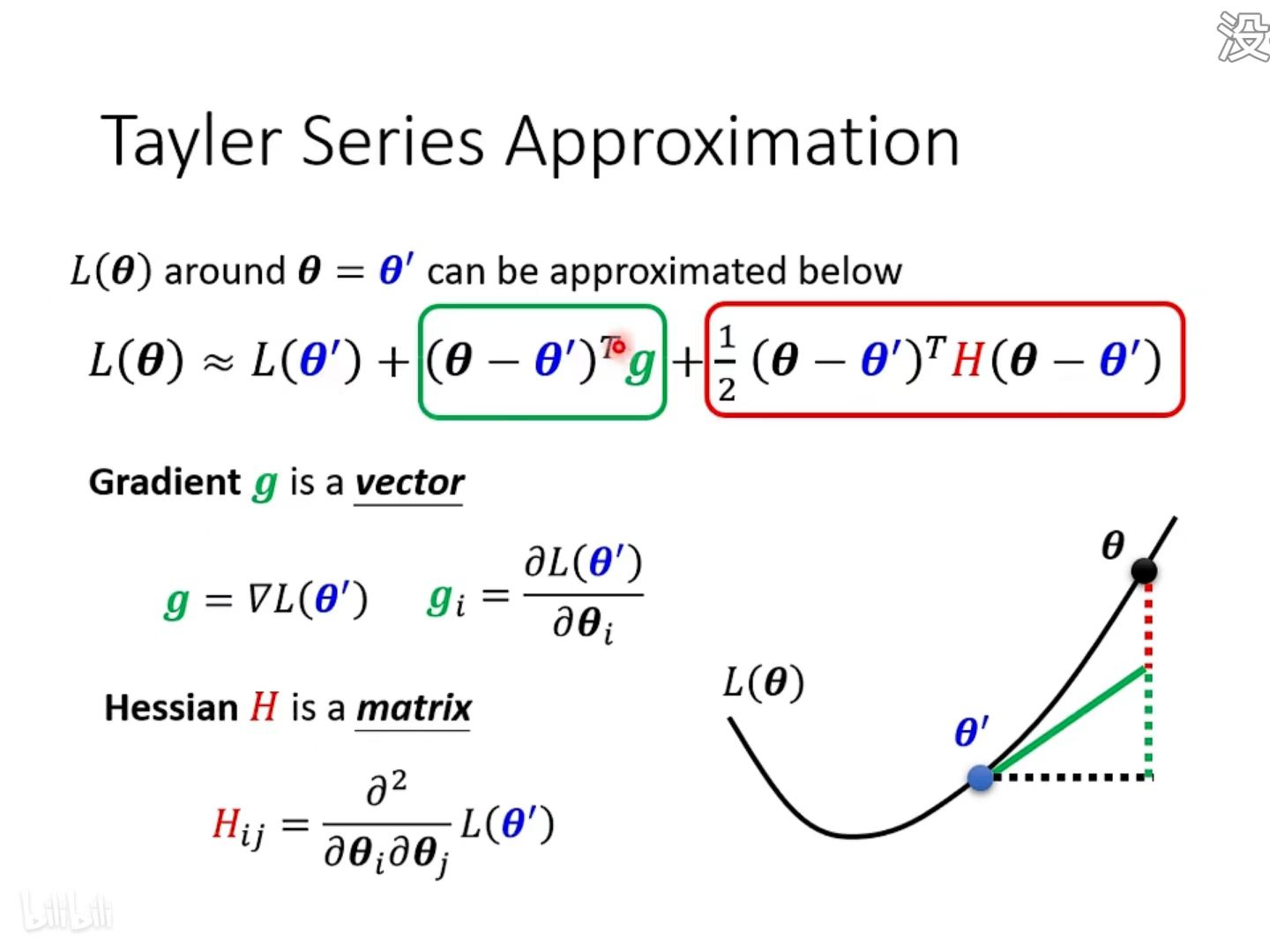
第一项中,L( θ ),当 θ 跟 θ ' 很近的时候,很靠近
第二项中,g 代表梯度(一阶导数),可以弥补 L( θ' ) 与 L( θ ) 之间的差距; g 的第 i 个component , 就是 θ 的第 i 个 component 对 L 的微分
第三项中,H 表示海塞矩阵,是 L 的二阶导数
在 Critical point 附近时:第二项为0,只需考察 H 的特征值
所有eigen value都是正的,H是positive definite (正定矩阵),此时是 local minima
所有eigen value都是负的,H是negative definite, L( θ' ) > L( θ ) ,此时 θ' 所处位置点是 local maxima
那如果eigen value有正有负,那就代表是 saddle point

如果走到鞍点,可以利用H的特征向量确定参数的更新方向,令 u = θ - θ',可以使用线性代数的思路,将矩阵 H 用特征值代替,一样可以求出当前位置点是 saddle point 还是 local minima / maxima,根据 θ = θ' + u 的公式求出下一个点所在位置,移动到该点 θ,这样可以使每一步移动都朝着能使 Loss 减小到最佳的效果

具体训练范例如下图所示,这是训练某一个 network 的结果,每一个点代表训练那个 network 训练完之后把它的 Hessian 拿出来进行计算。所以这边的每一个点都代表一个 network。
我们训练某一个network,然后把它不断的进行训练,直到到gradient很小,卡在critical point。然后把那组参数出来分析,看看它是saddle point 还是 local minima。
- 纵轴代表 training 的时候的 loss,就是卡住的那个loss。很多时候,loss在还很高的时候就训练不动了,卡在critical point;很多时候 loss 可以降得很低才卡在 critical point
- 横轴的部分是minimum ratio(最小比率)。minimum ratio是 eigen value 是正数的数目 / eigen value的总数目,如果所有的 eigen value 都是正的,代表我们今天的 critical point 是 local minima;如果有正有负代表 saddle point。(但是在实际操作中几乎找不到所有 eigen value 都是正的critical point)
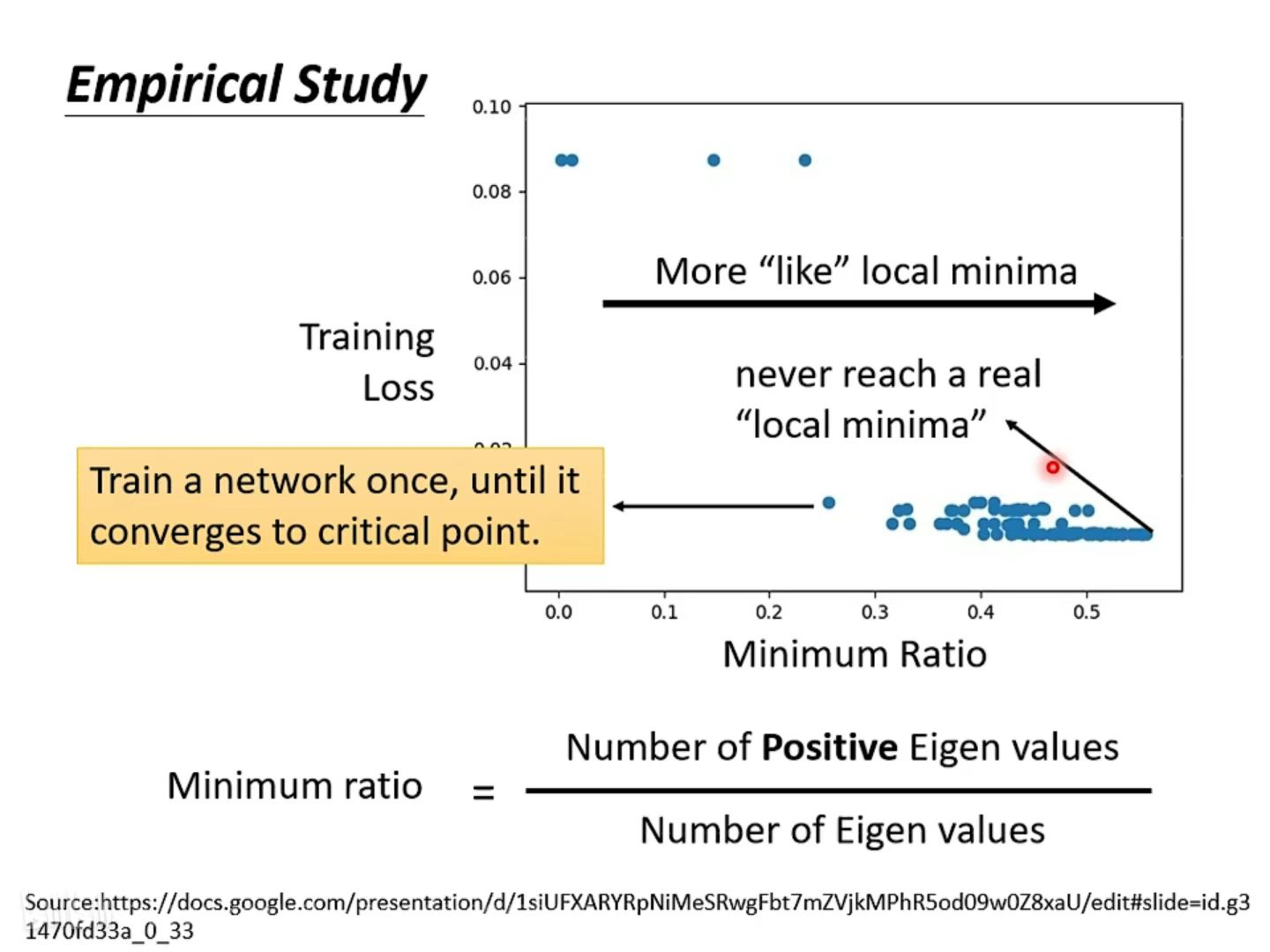
在这个图上,越往右说明 minimum ratio 越大,代表eigen value 是正数的数目比重更大,我们的 critical point 越像 local minima。但是它们都没有真的变成local minima,在下图的实际操作中,就算是在最极端右侧的状况,仍然有一半的 case 中 eigen value 是负的。这一半 case 的 eigen value 是正的,因此说明其实 local minima 并没有那么常见。多数的时候你觉得你train到一个地方,得到的gradient真的很小,从而参数不再 update 了,大概率就是卡在了 saddle point。
四、 解决卡在 critical point 的第一种办法:BatchSize (大小的选择与优缺点)
将一笔大型资料分若干批次计算 loss 和梯度,从而更新参数。每看完一个epoch 就把这笔大型资料打乱(shuffle),然后重新分批次。这样能保证每个 epoch 中的 batch 资料不同,避免偶然性。
1. 运算时间对比
设大批次含有20笔资料,小批次含有1笔资料,那么大批次就是看完20笔资料后再更新参数,而小批次则是看1笔资料就更新一次参数,总共更新20次。我们可以看到大批次的单次运算时间长但效果好,小批次的单次运算时间短但效果差,需要运算多次效果才好。

考虑 gpu “并行计算”,大的 BatchSize 并不一定时间比较长
刚刚讲的运算时间是针对单次更新,而在1 个 epoch 中,小批次反而耗时更长,大批次耗时更短。原因是:同样是60000笔资料,小批次要更新60000次,而大批次只要更新60次,更新速度又是差不多的,最后叠加起来肯定是大批次耗时更少。不过,GPU 平行运算的能力也有它的极限,当 Batch Size 真的非常非常巨大的时候,GPU 在跑完一个 Batch 后计算出 Gradient 所花费的时间,还是会随著 Batch Size 的增加而逐渐增长
总结:没有平行运算时,单次更新大批次耗时更长;有平行运算时,单次更新大小批次耗时差不多,而 1 个 epoch中大批次耗时更短。
2. 性能对比
小批次有更好的性能,由图可知同一个模型,同一个网络,training误差随着batch size 的增大而增大,testing 的误差也是。如果是 model bias 的问题,那么在 size 小的时候也会表现差,而不会等到 size 变大才差。所以这是Optimization issue(优化问题)导致大批次性能差。
①小批次有更好的性能
由图可知同一个模型,同一个网络,training 误差随着 batch size 的增大而增大,testing 的误差也是。根据之前学到的内容,如果是 model bias 的问题,那么在 BatchSize 小的时候也会表现差,而不会等到 size 变大才差。所以这是Optimization issue(优化问题)导致大批次性能差。
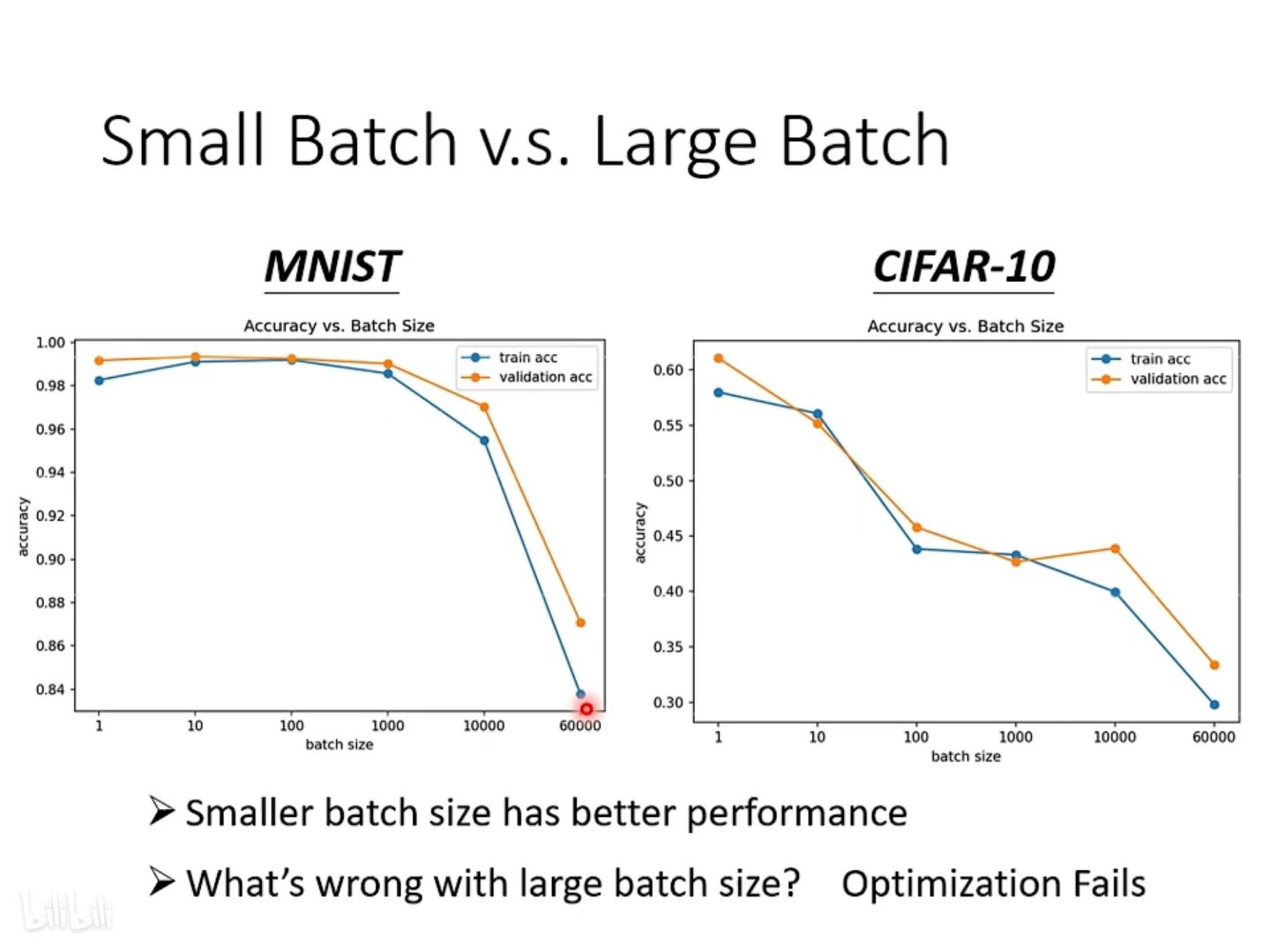
② 小批次在更新参数时会有 Noisy ⇒ 有利于训练
每次更新的时候,用的 loss 函数会有差异(如右图),因为不同的 batch 用不同的 loss function。换了个 loss 函数就更不容易卡住
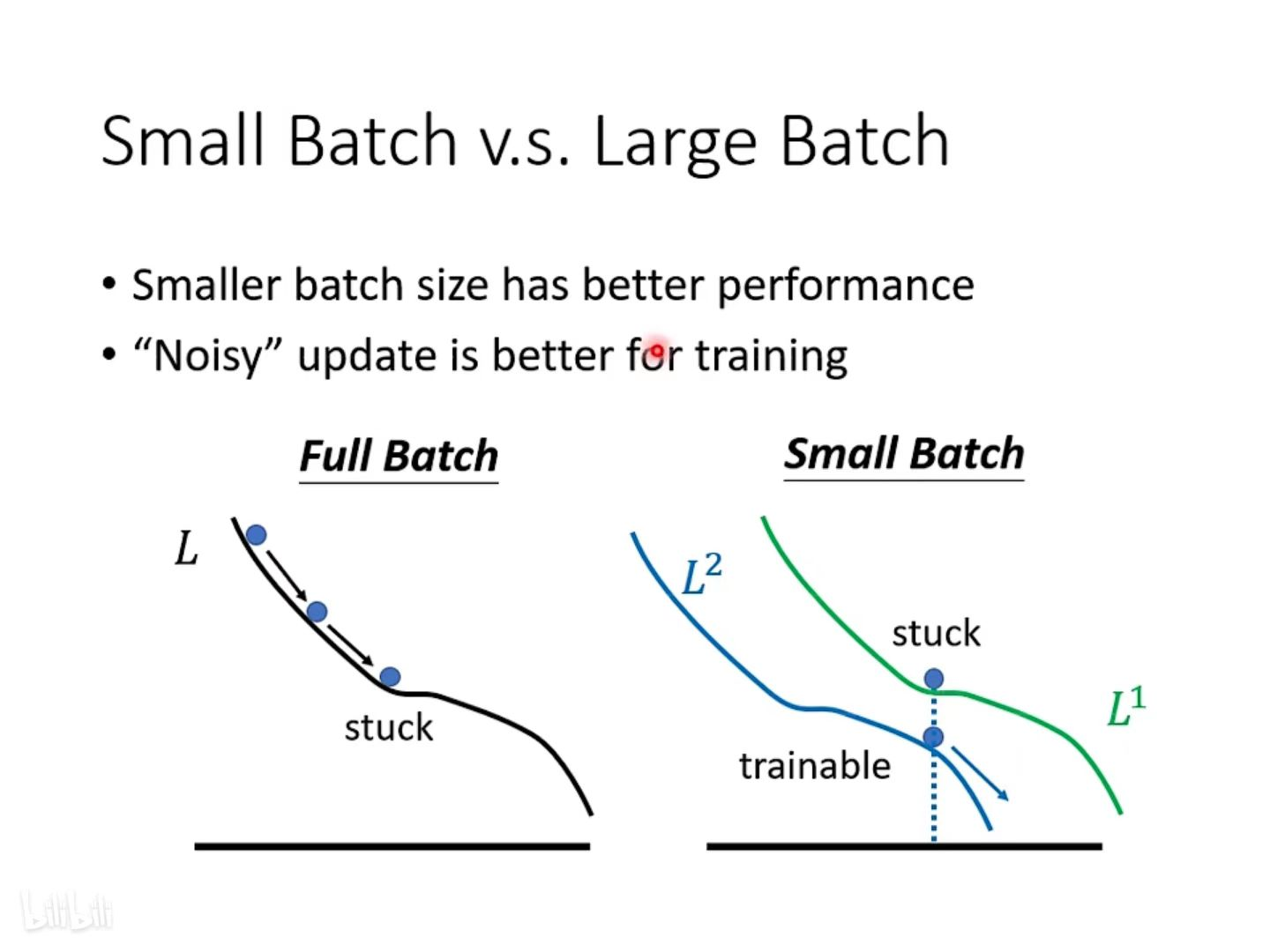
③ 小批次可以避免Overfitting ⇒ 有利于测试(Testing)
红框框中可以看出在训练时 SB(小批次)和 LB(大批次)的准确率都高,但是在咋样的0000testing 时,SB 的准确率还是比较高,而LB的准确率则更差点,此时 LB 面临的问题是 overfitting。
所以大批次在 training 时会遇到优化问题,而在 testing 时会遇到过拟合问题。
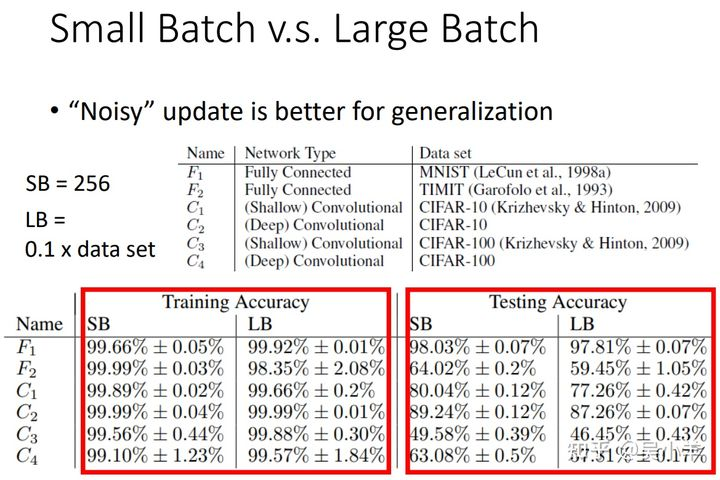
总结:对于 Batch size 而言,大和小都有各自的优势和劣势,所以 Batch size 的大小也就成了一个需要调整的 Hyperparameter,它会影响训练速度与优化效果。
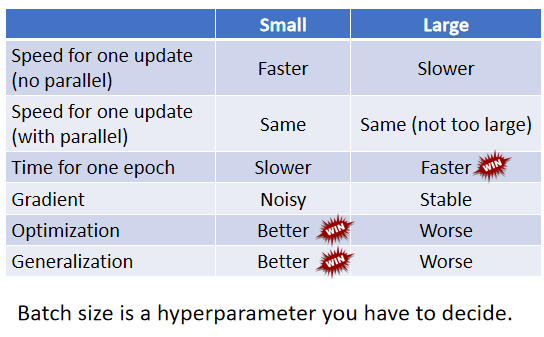
五. 解决卡在 critical point 的第二种办法
1. Momentum(动量)
在物理中,重物借用惯性,能够滚得更远。将这种思想应用于梯度下降中,能使参数在面临临界点时,能随着这种惯性越过越过当前局部最优值,避免训练中卡在 critical point (一般的梯度下降:往 梯度移动 的反方向 更新参数)
特点:在更新现在的梯度下降方向的时候,每一次仅利用 前一次 的梯度下降方向
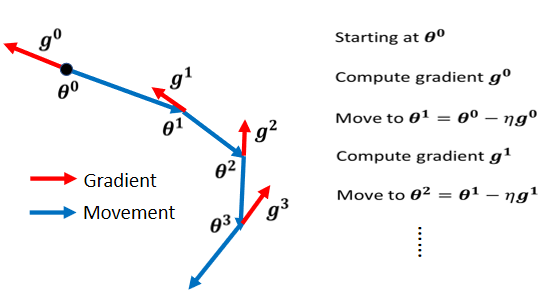
2. Gradient Descent + Momentum(考虑动量)⇒ 综合梯度 + 前一步的方向
① 特点:在更新现在的梯度下降方向的时候,考虑在此之前计算过的 所有的 梯度下降方向
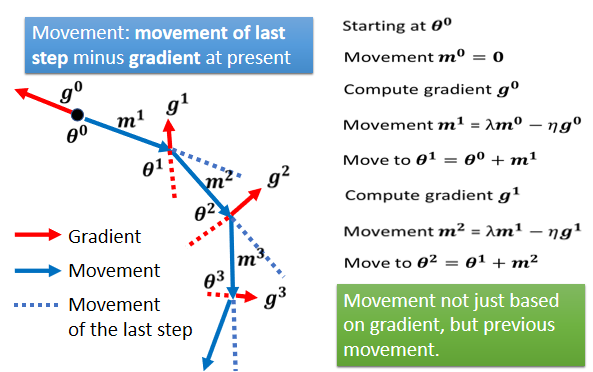
② 移动方向:梯度更新产生的距离和上一步产生的惯性距离之和。第三个球位于临界点,梯度更新产生的距离虽然是 0,但是还有上一步惯性距离,所以球能越过临界点,假如第四个球的上一步惯性距离大于梯度距离,则球可能可以越过山顶
六、解决卡在 critical point 的第三种办法 —— 自适应学习率调整(Adaptive Learning Rate)
1. introduction
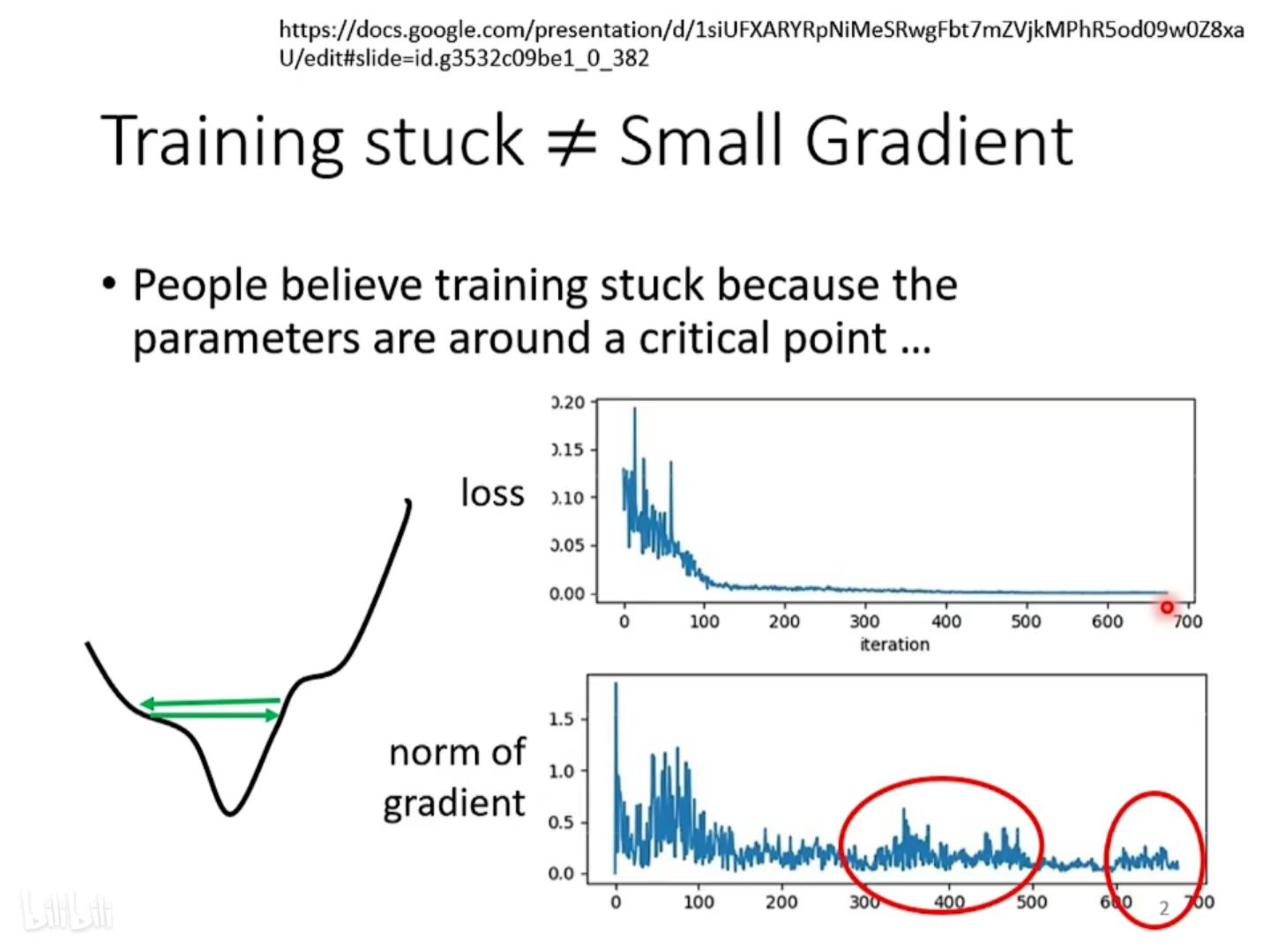
现象1:Training stuck ≠ Small Gradient
训练卡住的原因不一定是因为 gradient 太小,即critical point,也有可能是因为振荡。
如何看出是因为振荡导致训练 loss 降不下去:在训练过程中,gradient的大小有较大的波动(红色框中)。而产生振荡的原因就是 learning rate设定太大 。
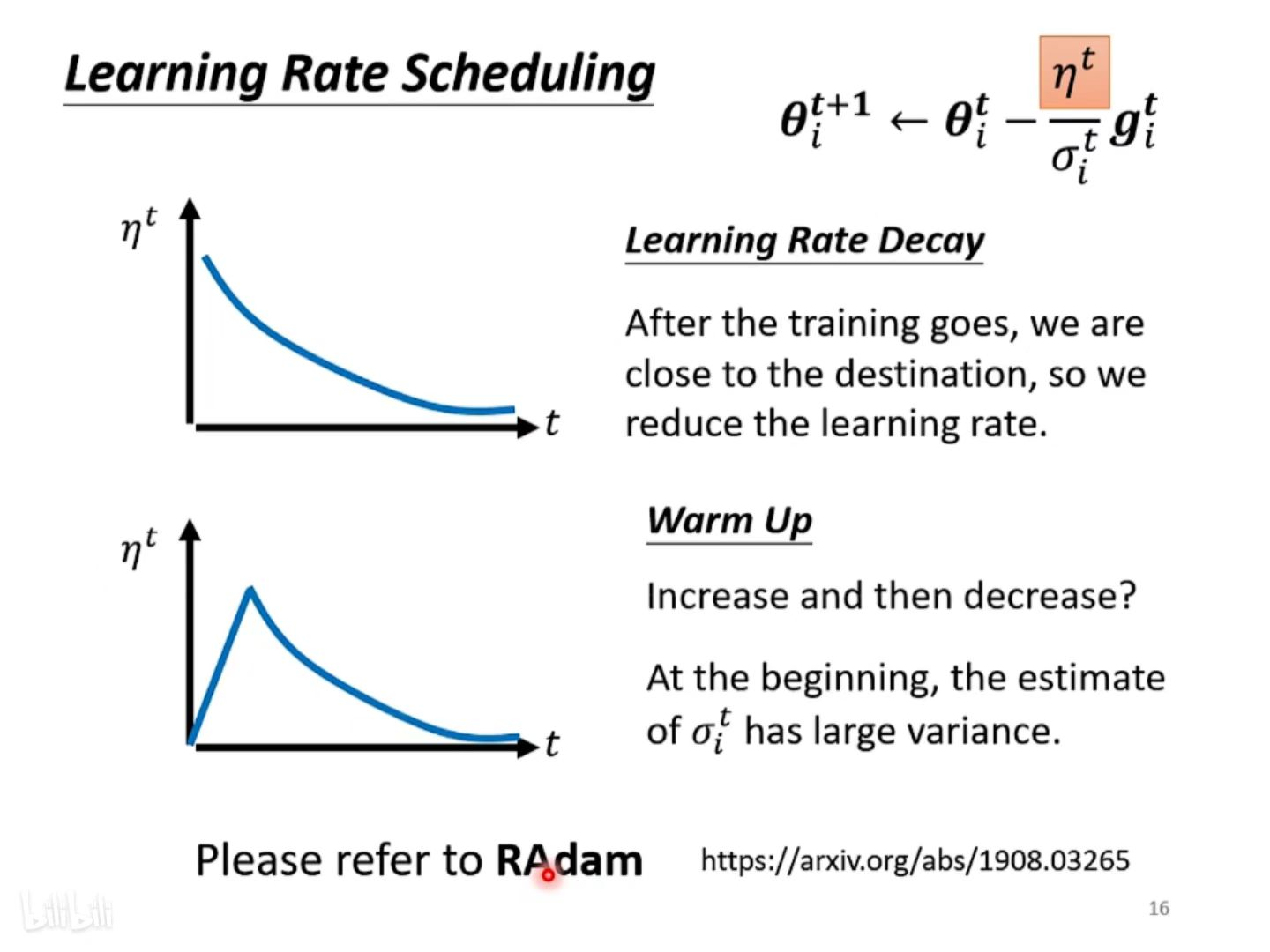
现象2:采用固定的学习率 将会很难达到最优解
及时不面对critical point问题,当采用固定的学习率 时,也将很难训练到最优解。
1)采用较大的学习率 时:会在最优解附近来回横跳。
2)采用较小的学习率 时:会在开始时向最优解较为稳定的移动,但是在靠近最优解后,会移动的十分缓慢。
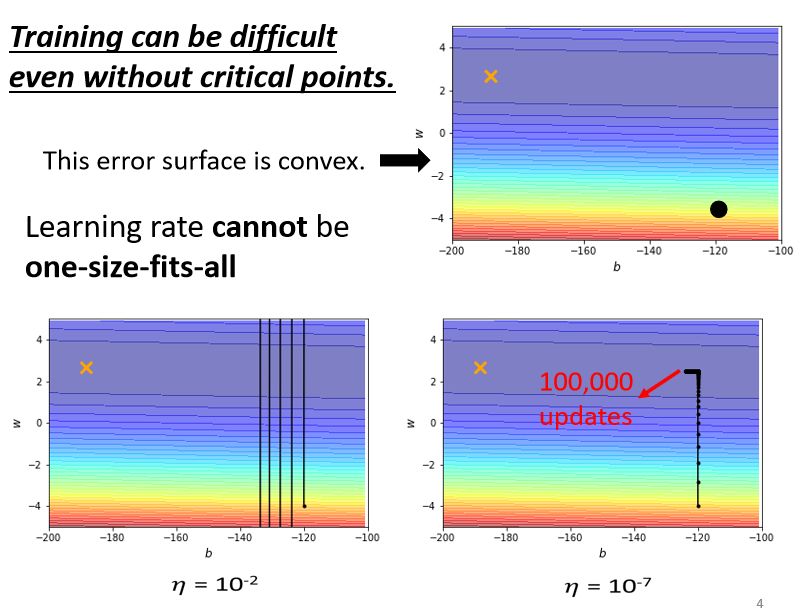
如上图举例:有个 error surface 是凸面,横轴参数的 loss 变化很小,而纵轴参数的 loss 变化快,坡度陡峭。黑点是初始点,叉叉是 loss 最低点。
假如设置个较大的 learning rate,纵轴参数更新时变化幅度大,会振荡;
假如设置个较小的 learning rate,纵轴参数能较好更新,而横轴参数却更新很慢,因为横轴坡度本来就平缓,再设个小的 lr 更新速度会更慢
总结:没有哪个 learning rate能一劳永逸,适应所有参数更新速度
2. 客制化“梯度” ⇒ 不同的参数(大小)需要不同的学习率
1)对于一个参数而言,使用常规的梯度下降法,参数更新方式为:
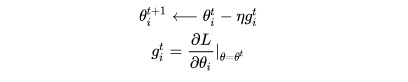
其中 表示
时刻参数
的数值,
表示学习率,
表示
时刻的梯度,
表示损失函数。
2)对于一个参数而言,使用自适应的学习率 的梯度下降法,参数更新的方式为:
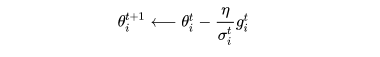
其中参数 是一个与参数
和时间
相关的参数。
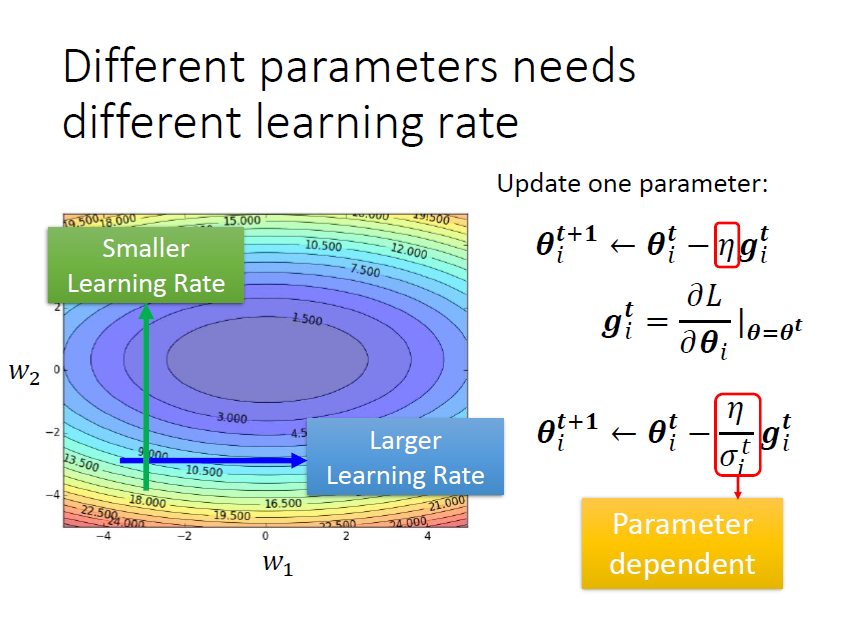
根据参数此时的实际情况,调整 的大小,实现对参数
的更新。
基本原则:
某一个方向上gradient的值很小,非常的平坦 ⇒ learning rate调大一点
某一个方向上非常的陡峭,坡度很大 ⇒ learning rate可以设得小一点
3. 求取的方式
① Root Mean Square
整体思路:将历史梯度绝对值的大小进行考虑(可以理解为过往梯度的平均值),使得随着网络的训练,learning rate的值越来越小,从而保证梯度在不断的训练过程中越来越小,达到最终收敛的目的,防止在最优解附近来回横跳。
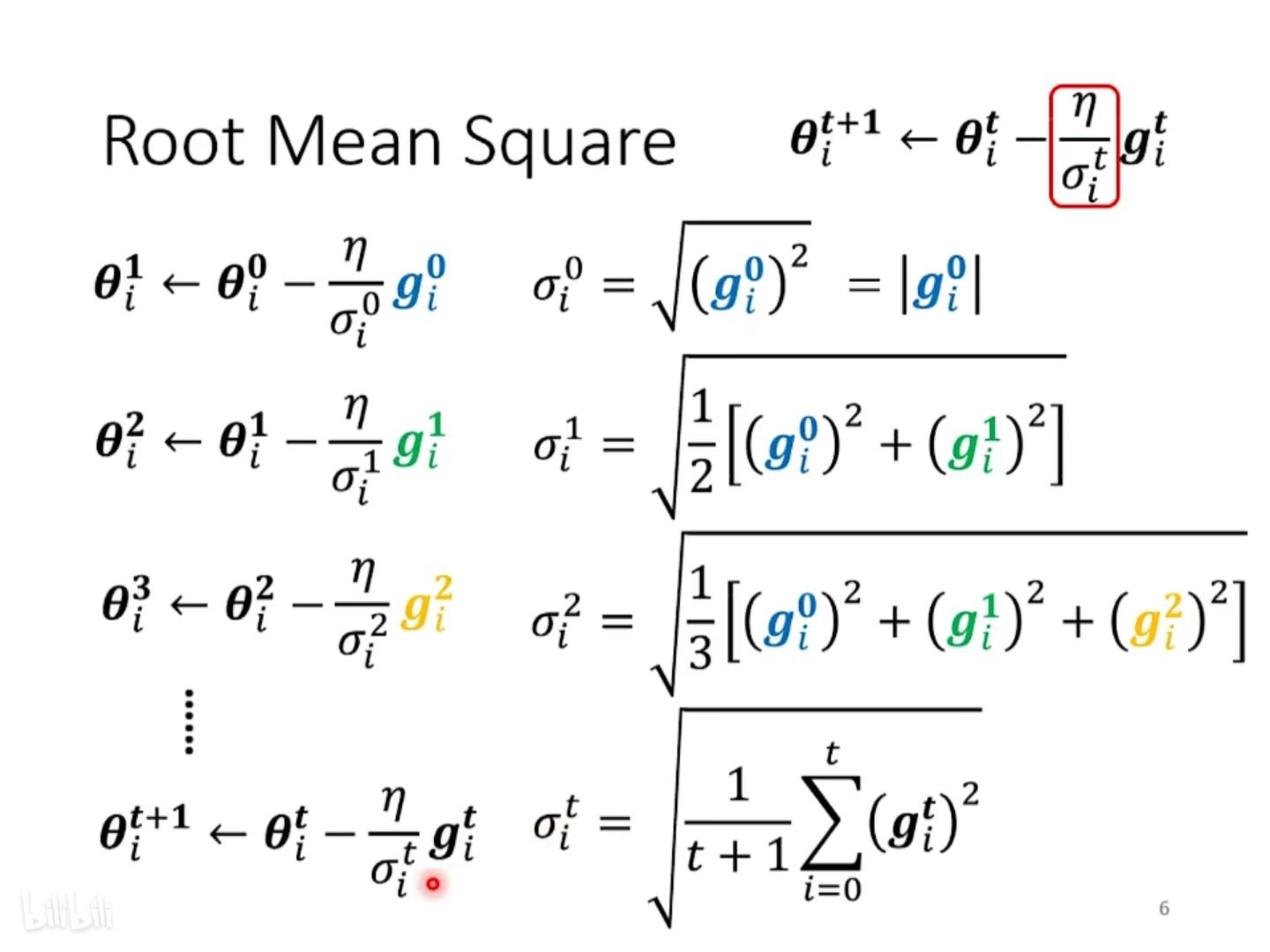
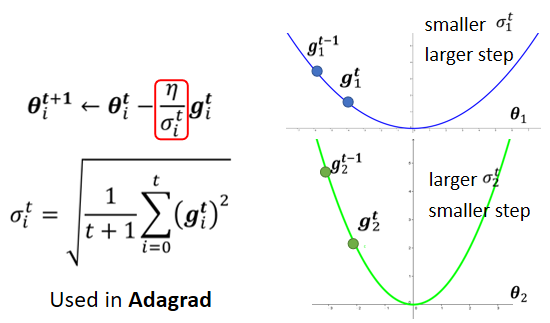
将 Root Mean Square 的思路方式使用在 Adagrad 中。
gradient 比较大(Loss 趋于陡峭),σ 就比较大 , 在 update 的时候 参数 update 的步长就比较小;gradient 比较小(Loss 趋于平缓),σ 就比较大 , 在 update 的时候 参数 update 的步长就比较大。
缺点:不能 “实时” 考虑梯度的变化情况
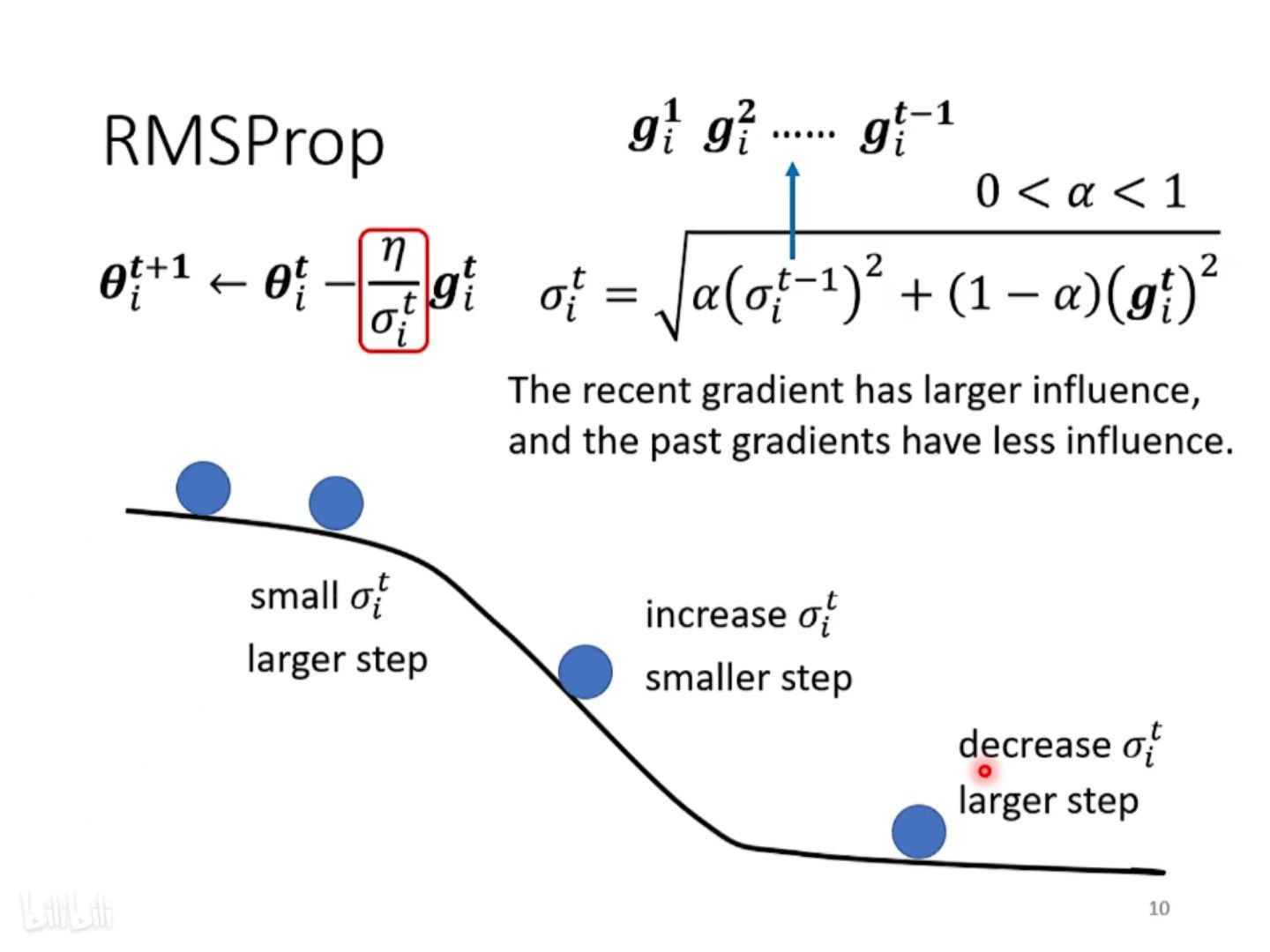
② RMS Prop —— 调整 “当前步” 梯度 与 “历史” 梯度的比重关系
整体思路:Root Mean Square方式中,learning rate随着训练不断降低,可以达到梯度随着训练逐步降低,最终达到收敛的效果。然而当一个参数在训练过程中,其梯度的大小往往会出现实大实小的情况,这个时候需要在梯度较小时采用较大的 learning rate,在梯度较大时采用较小的learning rate,从而保证正确而快速的收敛。
方法:添加参数 (表示当前梯度大小对于 learning rate 的影响比重,是一个超参数(hyperparameter)
- α 设很小趋近於0,就代表这一步算出的 gᵢ 相较于之前所算出来的 gradient 而言比较重要
- α 设很大趋近於1,就代表现在算出来的 gᵢ 比较不重要,之前算出来的 gradient 比较重要
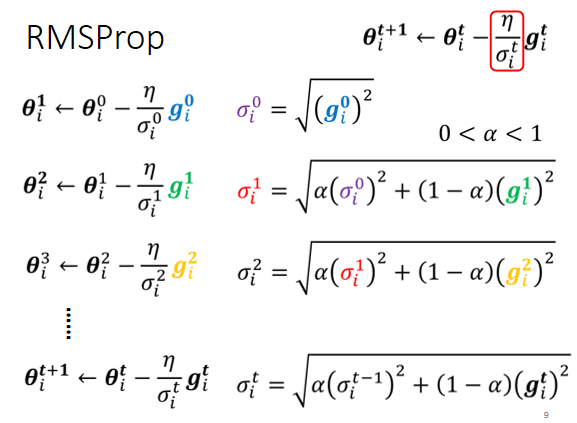
③ 最常用的策略:Adam = RMSProp + Momentum

论文链接:https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1412.6980.pdf,其中使用 Pytorch 预设的参数就会有很好的效果
4. 求取 的方式
上述方案容易出现的问题:如果单纯的将 learning rate 的 中的
部分进行使用动态调整,每次都将之前的梯度结果进行综合考虑,就会导致当梯度值的变化若是开始大、后来小时,当小梯度积累到一定程度时,由于
是一个指数为 -1 的幂函数,下降速度极快,其结果很快就会小于
值,而
也是一个指数为-1的幂函数,导致整体的 learning rate 极速增加,从而发生抖动,但随着新的大梯度的加入,会使得逐渐learning rate降低,最终梯度逐渐平稳。
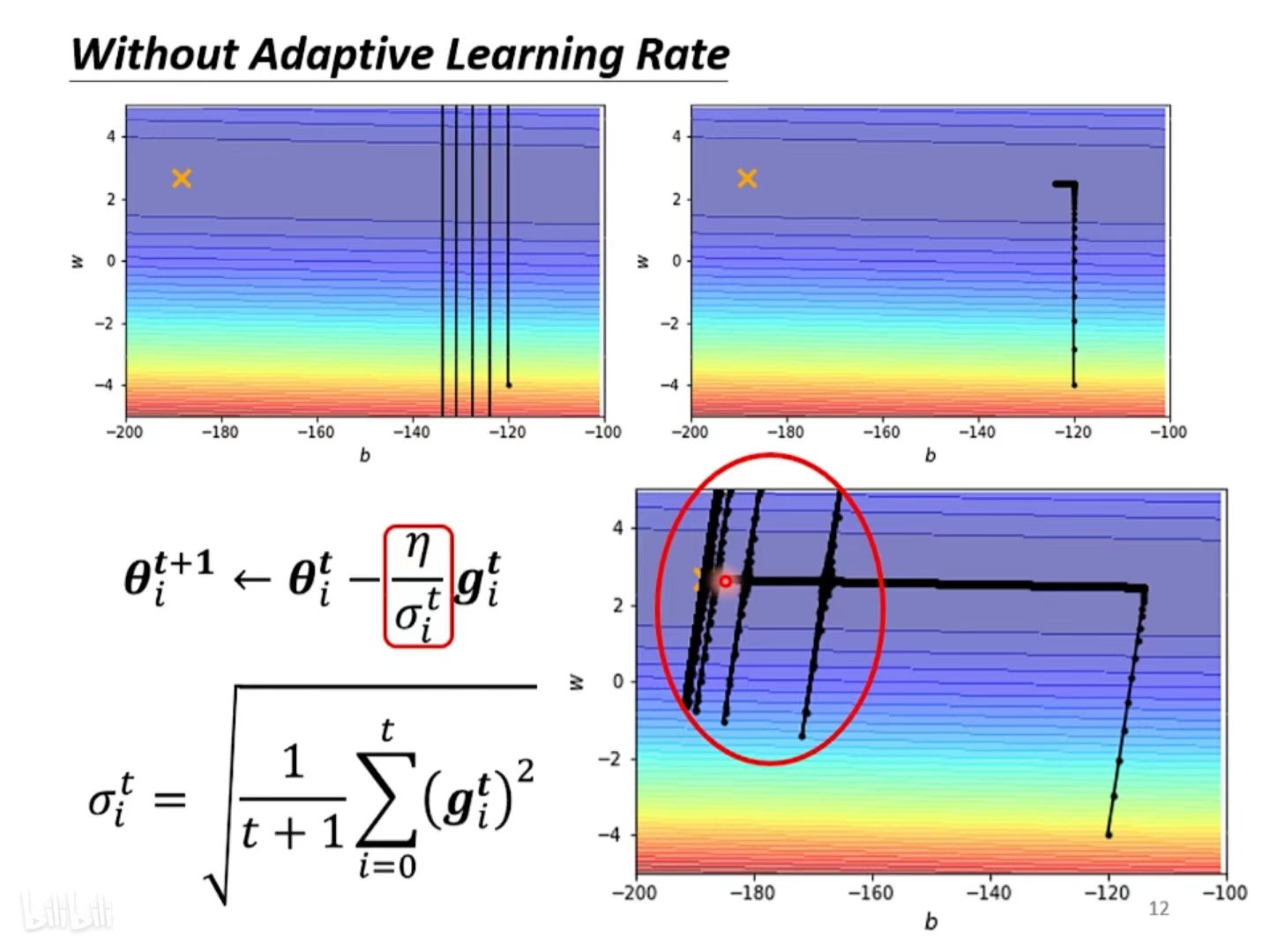
解决方法:Learning Rate Scheduling ⇒ 让 LearningRate 与 “训练时间” 有关
具体思路:当 在低谷中累积减小时,
也在慢慢减小,所以可以使得
的整体变大趋势不明显,步伐也不会太大导致喷发。理想的情况是,随之训练的进行,会越来越接近目的地,所以我们希望 learning rate 能随着时间慢慢降低,从而使得在接近目的地时移动步伐能够缓慢前进,避免幅度太大导致出现抖动现象。
因此,我们需要将分子 也进行调整,将其升级为与时间相关的一个变量
(使用 Warm Up的方式,随着时间先变大后变小)
指示某一个方向有多陡 / 平滑,这个统计的结果要看很多组数据以后才能够计算精准,所以在起初计算 error surface 陡峭 / 平缓状态不太精准(统计整体梯度不够有代表性)的情况下,设置的 learning rate 应该比较小,目的是为了能够限制参数不会走的离初始的地方太远,从而慢慢地探索并收集更多有关 error surface 的状态信息,等到
统计得比较精準以后再让 learning rate慢慢提升。
5. 优化总结
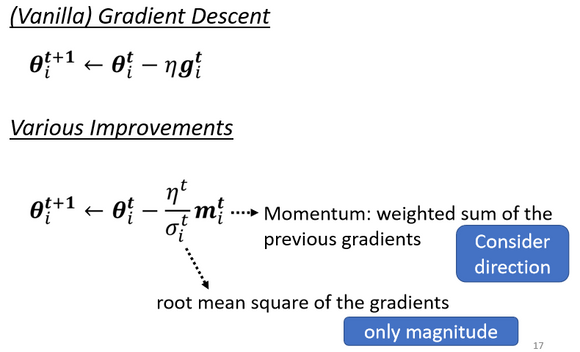
① 使用动量,考虑过去梯度的 “大小” 与 “方向”
② 引入 ,考虑过去梯度的 “大小” (RMSProp)
③ 使用 LearningRate Schedule,调整 让 LearningRate 与 “训练时间” 有关
七、 classification 与 regression 的区别
通过以往学习已经知道:
1. 在输出数量方面, R 只输出一个预测 y 值,而C 通过 one-hot vector(独热编码)表示不同的类别(一个向量中只有1 个 1 ,其余都为 0,1 在不同的位置代表不同类别);
2. 在计算 Loss 时,R 直接拿预测输出数值 y 和 真实数值 计算接近度,而 C 将多个输出数值组成一个向量,向量经过 softmax(归一化,保证输出 y′ 在 0 与 1 之间,并且总和为1,可以理解为 预测输出是 yi 所代表类别的的概率值) 后形成新的向量,再拿新的向量去和不同类别计算接近度。
3. 计算loss的方法不同(新学习的)
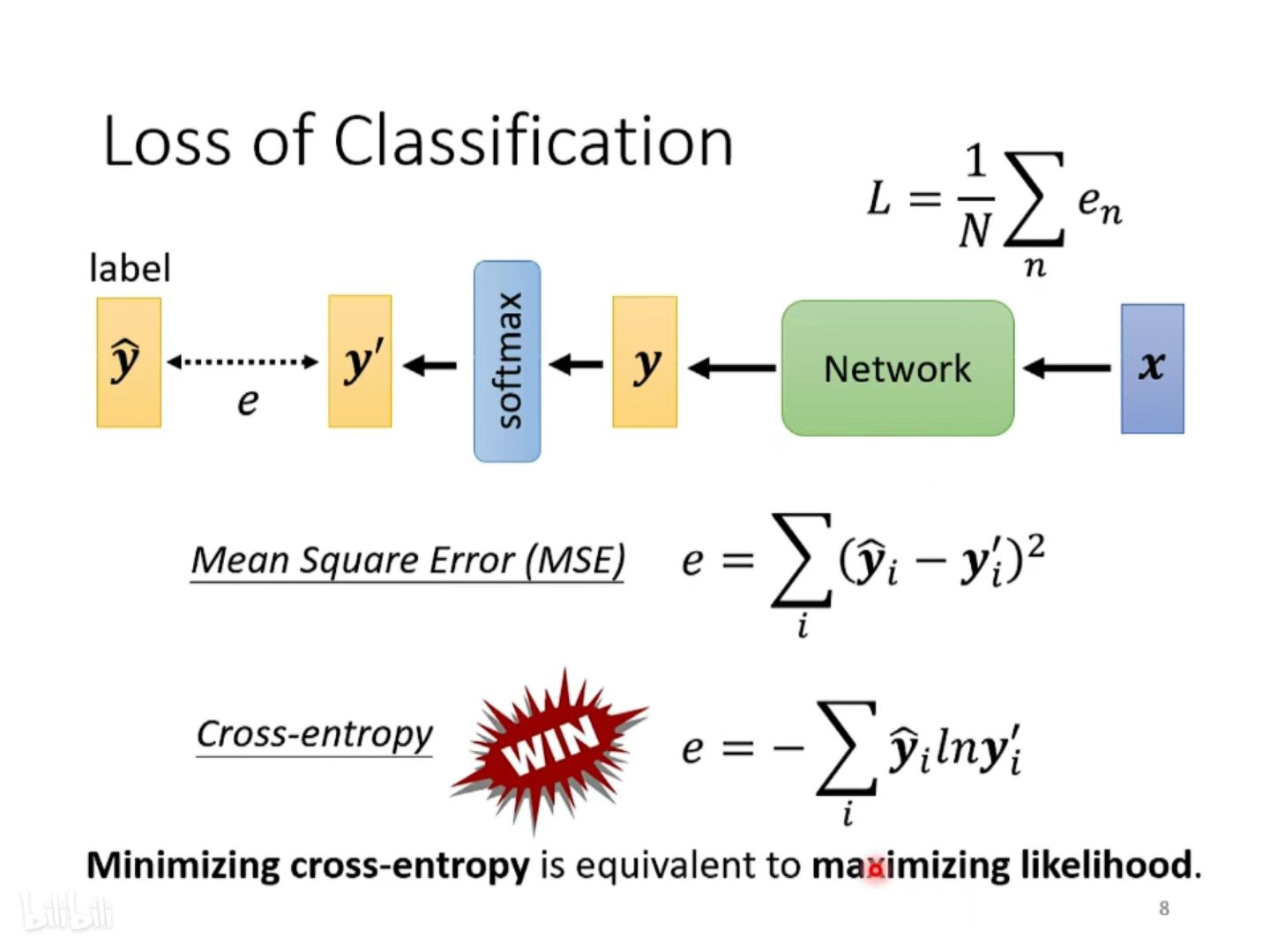
① 介绍: regression 采用 MSE 和 MAE 的方法计算 loss 函数;而 classification 采用 cross entropy(交叉熵)的方法计算 loss 函数,当 ŷ 跟 y' 一模一样的时候,为最小交叉熵(等价于 maximizing likelihood 最大似然估计)
② 交叉熵适用于 classification 的原因:交叉熵改变了 loss 函数,也就改变了 error surface,使得在大 loss 的地方也会有大的 gradient,而不像 MSE 在大 loss 处的 gradient 很小,不易梯度下降。所以交叉熵计算出来的loss函数更容易做梯度下降,不容易卡在 critical point
P.S. 在 pytorch 中,softmax 是嵌在 cross entropy 里面的,所以用了 cross entropy 就不用加 softmax 了,否则就有两层 softmax



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布:重大改进与新特性概览!
· .NET10 - 预览版1新功能体验(一)