刷题笔记8.贪心算法/背包问题
贪心算法
1)最自然智慧的算法
2)用一种局部最功利的标准,总是做出在当前看来是最好的选择
3)难点在于证明局部最功利的标准可以得到全局最优解
4)对于贪心算法的学习主要以增加阅历和经验为主

贪心算法和动态规划的区别:


适用于贪心算法的场景

背包问题
一篇文章吃透背包问题!(细致引入+解题模板+例题分析+代码呈现) - 零钱兑换 - 力扣(LeetCode) (leetcode-cn.com)
322. 零钱兑换
1.动态规划
动态规划从 memo[0] 开始,从下到上

我们采用自下而上的方式进行思考。仍定义 F(i)F(i) 为组成金额 ii 所需最少的硬币数量,假设在计算 F(i) 之前,我们已经计算出 F(0)-F(i-1) 的答案。 则 F(i)对应的转移方程应为
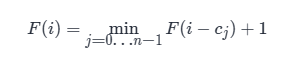
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
int max=amount+1;
Arrays.fill(dp, max);
dp[0] = 0;
for(int i=1;i<=amount;i++){
for(int c:coins){
if(i-c>=0)
dp[i]=Math.min(dp[i-c]+1,dp[i]);
}
}
if(dp[amount]==amount+1) return -1;
return dp[amount];
}
}
2.记忆化搜索(回溯)
记忆化搜索是先从 memo[amonut-1]开始,从上到下
-
这种找路径,找方法的题一般可以使用回溯法来解决,回溯法也可以说是树形图法,解题的时候使用类似于树状图的结构,使用 自顶而下 的方法。
-
而在回溯法中,如果含有很多的重复的计算的时候,就可以使用记忆化的搜索,将可能出现的重复计算大状态使用一个数组来保存其值,在进行重复的计算的时候,就可以直接的调用数组中的值,较少了不必要的递归。
可以看出在进行递归的时候,有很多重复的节点要进行操作,这样会浪费很多的时间。
使用数组memo[ ] 来保存节点的值
memo[n] 表示钱币 n 可以被换取的最少的硬币数,不能换取就为 -1
dfs函数的目的是为了找到 amount 数量的零钱可以兑换的最少硬币数量,返回其值 int在进行递归的时候,memo[n]被复制了,就不用继续递归了,可以直接的调
class Solution {
int[] memo;
public int coinChange(int[] coins, int amount) {
if(coins.length == 0){
return -1;
}
memo = new int[amount];
return findWay(coins,amount);
}
// memo[n] 表示钱币n可以被换取的最少的硬币数,不能换取就为-1
// findWay函数的目的是为了找到 amount数量的零钱可以兑换的最少硬币数量,返回其值int
public int findWay(int[] coins,int amount){
if(amount < 0){
return -1;
}
if(amount == 0){
return 0;
}
// 记忆化的处理,memo[n]用赋予了值,就不用继续下面的循环
// 直接的返回memo[n] 的最优值
if(memo[amount-1] != 0){
return memo[amount-1];
}
int min = Integer.MAX_VALUE;
for(int i = 0;i < coins.length;i++){
int res = findWay(coins,amount-coins[i]);
if(res >= 0 && res < min){
min = res + 1; // 加1,是为了加上得到res结果的那个步骤中,兑换的一个硬币
}
}
memo[amount-1] = (min == Integer.MAX_VALUE ? -1 : min);
return memo[amount-1];
}
}
860. 柠檬水找零
方法一:贪心
由于顾客只可能给你三个面值的钞票,而且我们一开始没有任何钞票,因此我们拥有的钞票面值只可能是 5美元,101美元和 20 美元三种。基于此,我们可以进行如下的分类讨论。
-
5美元,由于柠檬水的价格也为 5 美元,因此我们直接收下即可。
-
10美元,我们需要找回 5美元,如果没有 5美元面值的钞票,则无法正确找零。
-
20美元,我们需要找回 15美元,此时有两种组合方式,一种是一张 10 美元和 5 美元的钞票,一种是 3 张 5 美元的钞票,如果两种组合方式都没有,则无法正确找零。当可以正确找零时,两种找零的方式中我们更倾向于第一种,即如果存在 5 美元和 10 美元,我们就按第一种方式找零,否则按第二种方式找零,因为需要使用 5美元的找零场景会比需要使用 10 美元的找零场景多,我们需要尽可能保留 5 美元的钞票。
class Solution {
int memo;
public boolean lemonadeChange(int[] bills) {
int five=0;
int ten=0;
for(int bill : bills){
if(bill==5){
five++;
}else if(bill==10){
if(five==0){
return false;
}else{
five--;
ten++;
}
}else if(bill==20){
if(ten>0&&five>0){
five--;
ten--;
}else if(ten==0&&five>=3){
five=five-3;
}else{
return false;
}
}
}
return true;
}
}
122. 买卖股票的最佳时机 II
贪心
455. 分发饼干
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int numOfChildren = g.length, numOfCookies = s.length;
int count = 0;
for (int i = 0, j = 0; i < numOfChildren && j < numOfCookies; i++, j++) {
while (j < numOfCookies && g[i] > s[j]) {
j++;
}
if (j < numOfCookies) {
count++;
}
}
return count;
}
}
874. 模拟行走机器人
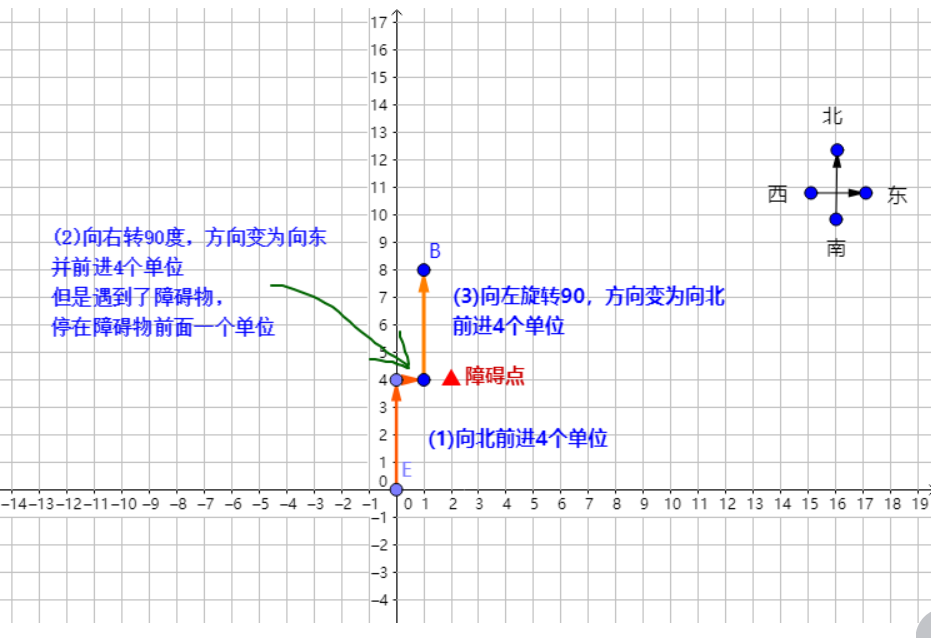
1.分解机器人行走
走k步,就是朝着一个方向走k个1步
怎么朝着某个方向走出一步
方向向北,机器人坐标点向上走一步
方向向东,机器人坐标点向右走一步
方向向南,机器人坐标点向下走一步
方向向西,机器人坐标点向上左一步
int direx[] = {0,1,0,-1};
int direy[] = {1,0,-1,0};
direx[],direy[] 要竖着对齐看
- 向北,坐标轴上x不动,y+1, 即(0,1)
- 向东,坐标轴上x+1,y不动, 即(1,0)
- 向南,坐标轴上x不动,y-1, 即(0,-1)
- 向西,坐标轴上x-1,y不动, 即(-1,0)
2.机器人如何调整方向
direx[]direy[] 的下标 i 代表了当前机器人的方向
- i=0,向北
- i=1,向东
- i=2,向南
- i=3,向西
当读取到调整方向的指令时,如
"-1":“向右转90度”,只要当前方向curdire + 1就可以得到右转方向
"-2":“向左转90度”,只要当前方向curdire + 3 就可以得到左转方向 (curdire + 3) % 4,
因为不管curdire当前是哪个方向,左转都在其左边,在direx数组的定义中顺势针数3个就是其左边,所以就是加3
3.怎么判断是否遇到了障碍物
障碍物有多个,所以需要有一个障碍物坐标点集合
机器人每试图走一个位置,就用此位置与障碍物集合列表里的坐标进行比较,看是否刚好是障碍物坐标点
- 不是,则“真正走到这个点”,更新机器人坐标点(curx,cury)
- 是障碍物,那么不走下一步,停留在当前,执行下一条命令
class Solution {
public int robotSim(int[] commands, int[][] obstacles) {
int result = 0;
int x = 0, y = 0, direction = 0;
int[] directX = new int[]{0, 1, 0, -1};
int[] directY = new int[]{1, 0, -1, 0};
// 用 set 存储障碍物的坐标
Set<String> obstaclesSet = new HashSet<String>();
for (int i = 0; i < obstacles.length; i++) {
obstaclesSet.add(obstacles[i][0] + "," + obstacles[i][1]);
}
for (int com : commands) {
if (com == -2) {
// turn left
direction = (direction + 3) % 4;
} else if (com == -1) {
// turn right
direction = (direction + 1) % 4;
} else {
for (int i = 1; i <= com; i++) {
// 下一步的坐标
int newX = x + directX[direction];
int newY = y + directY[direction];
// 遇到障碍物,停止前进
if (obstaclesSet.contains(newX + "," + newY)) {
break;
}
// 前进
x = newX;
y = newY;
// 最大欧式距离的平方
result = Math.max(result, x * x + y * y);
}
}
}
return result;
}
}
55. 跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
1.贪心算法
这样以来,我们依次遍历数组中的每一个位置,并实时维护 最远可以到达的位置。对于当前遍历到的位置 x,如果它在 最远可以到达的位置 的范围内,那么我们就可以从起点通过若干次跳跃到达该位置,因此我们可以用$ x + \textit{nums}[x] $更新 最远可以到达的位置。
在遍历的过程中,如果 最远可以到达的位置 大于等于数组中的最后一个位置,那就说明最后一个位置可达,我们就可以直接返回 True 作为答案。反之,如果在遍历结束后,最后一个位置仍然不可达,我们就返回 False 作为答案。
我们再来看看题目中的示例二
-
[3, 2, 1, 0, 4]
-
我们一开始在位置 0,可以跳跃的最大长度为 3,因此最远可以到达的位置被更新为 3;
-
我们遍历到位置 1,由于 1≤3,因此位置 1 可达,加上它可以跳跃的最大长度 2 得到 3,没有超过最远可以到达的位置;
-
位置 2、位置 3同理,最远可以到达的位置不会被更新;
-
我们遍历到位置 4,由于 4 > 3,因此位置 4 不可达,我们也就不考虑它可以跳跃的最大长度了
public class Solution {
public boolean canJump(int[] nums) {
int n = nums.length;
int rightmost = 0;
for (int i = 0; i < n; ++i) {
if (i <= rightmost) {
rightmost = Math.max(rightmost, i + nums[i]);
if (rightmost >= n - 1) {
return true;
}
}
}
return false;
}
}
2.动态规划
这个题我们可以从后往前分析,首先判断倒数第二个元素能否到达最后一个元素,如果可以,我们将不再考虑最后一个元素,
因为根据刚才的分析如果可以到达倒数第二个,那么也可以到达最后一个元素。
然后依次往前递推,如果都能跳到的话,我们最后应该分析的就是第一个元素能否跳到第二个元素上。
class Solution {
public boolean canJump(int[] nums) {
boolean[] dp=new boolean[nums.length];
dp[0]=true;
for(int i=1;i<nums.length;i++){
for (int j = 0; j < i; j++) {
// 如果之前的j节点可达,并且从此节点可以到跳到i
if (dp[j] && nums[j] + j >= i) {
dp[i] = true;
break;
}
}
}
return dp[nums.length-1];
}
}
45. 跳跃游戏 II
1.反向遍历
我们的目标是到达数组的最后一个位置,因此我们可以考虑最后一步跳跃前所在的位置,该位置通过跳跃能够到达最后一个位置。
如果有多个位置通过跳跃都能够到达最后一个位置,那么我们应该如何进行选择呢?直观上来看,我们可以「贪心」地选择距离最后一个位置最远的那个位置,也就是对应下标最小的那个位置。因此,我们可以从左到右遍历数组,选择第一个满足要求的位置。
找到最后一步跳跃前所在的位置之后,我们继续贪心地寻找倒数第二步跳跃前所在的位置,以此类推,直到找到数组的开始位置
class Solution {
public int jump(int[] nums) {
int position =nums.length-1;
int step=0;
while(position>0){
for(int i=0;i<position;i++){
if(nums[i]+i>=position){
position=i;
step++;
break;
}
}
}
return step;
}
}
2.正向查找可到达的最大位置
例如,对于数组 [2,3,1,2,4,2,3],初始位置是下标 0,从下标 0 出发,最远可到达下标 2。下标 0 可到达的位置中,下标 1 的值是 3,从下标 1 出发可以达到更远的位置,因此第一步到达下标 1。
从下标 1 出发,最远可到达下标 4。下标 1 可到达的位置中,下标 4 的值是 4 ,从下标 4 出发可以达到更远的位置,因此第二步到达下标 4。
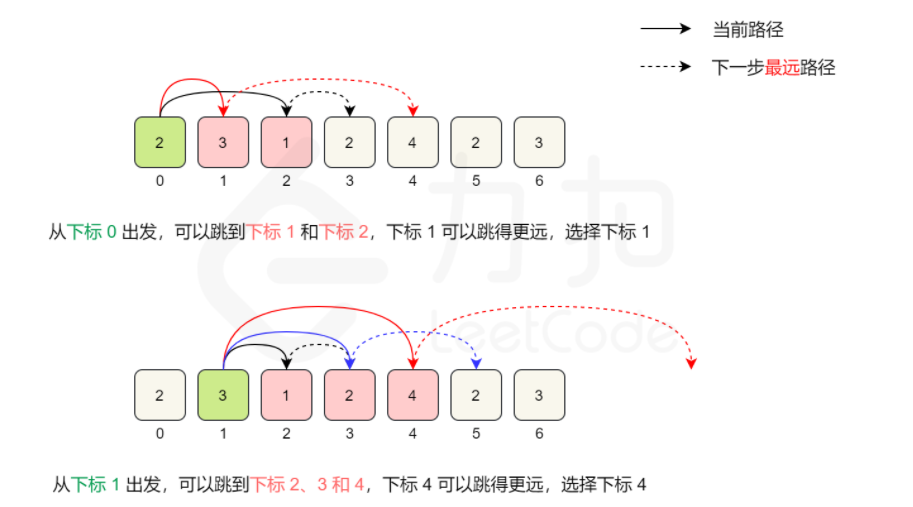
在具体的实现中,我们维护当前能够到达的最大下标位置,记为边界。我们从左到右遍历数组,到达边界时,更新边界并将跳跃次数增加 1。
在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了。如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次数」,因此我们不必访问最后一个元素。
class Solution {
public int jump(int[] nums) {
//一次跳跃的结尾
int end =0;
int maxPosition =0;
int step=0;
for(int i=0;i<nums.length-1;i++){
maxPosition = Math.max(maxPosition, i + nums[i]);
//一次跳跃完成更新下次跳跃的结尾
if(i==end){
end = maxPosition;
step++;
}
}
return step;
}
}
3.动态规划
class Solution {
public int jump(int[] nums) {
if(nums.length==1) return 0;
int[] dp=new int[nums.length];
dp[0]=0;
dp[1]=1;
for(int i=1;i<nums.length;i++){
int min=Integer.MAX_VALUE;
for(int j=0;j<i;j++){
if(nums[j]+j>=i){
min=Math.min(min,dp[j]+1);
break;
}
}
dp[i]=min;
}
return dp[nums.length-1];
}
}



