刷题笔记4.栈、队列、优先队列、双端队列
栈、队列、优先队列、双端队列
参考链接
栈Stack
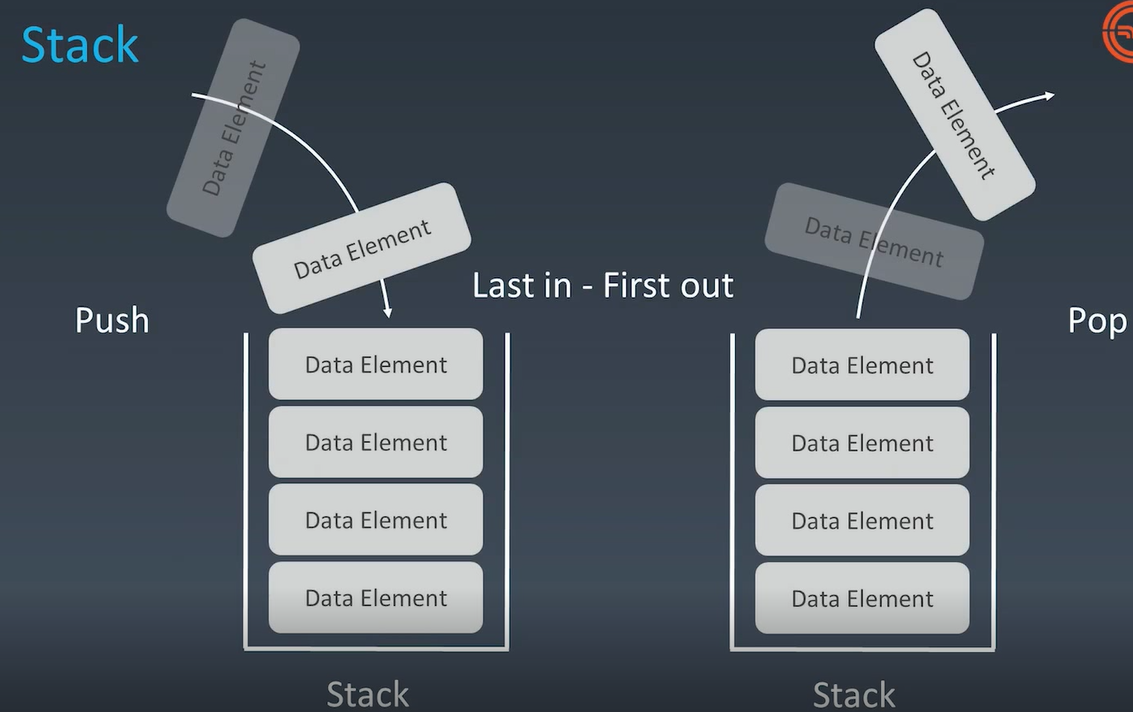
Stack Integer> stack = new Stack<>();stack. push(1);
stack. push(2);
stack push(3);
stack. push(4);
System out. println(stack);
System out. println(stack search(4));
stack. pop();
stack pop();
Integer topElement = stack peek();
System out println (topElement);
System out. println(" 3的位置 " + stack search(3));
队列Queue

Stack:先入后出,o(1)
Queue:先入先出,o(1)
//双向队列:
Deque<Integer> levelList = new LinkedList<Integer>();
levelList.offerLast(curNode.val);//尾插
levelList.offerFirst(curNode.val);//头插
//队列:
Queue<TreeNode> queue = new LinkedList<>();
TreeNode tmp = queue.poll();
queue.offer(root);
//双向链表:
LinkedList<Integer> path = new LinkedList<>();
path.addFirst(tmp.val);//头插
path.addLast(tmp.val);//尾插
双端队列Deque
实战中,一般用双端队列实现栈和队列,Stack和Queue的结合


优先队列

PriorityQueue<ListNode> queue = new PriorityQueue<>(lists.length, new Comparator<ListNode>() {
@Override
public int compare(ListNode o1, ListNode o2) {
if (o1.val < o2.val) return -1;
else if (o1.val == o2.val) return 0;
else return 1;
}
});
queue.add(node)
queue.isEmpty()
queue.poll()
实战题目
20. 有效的括号
1.栈
class Solution {
public boolean isValid(String s) {
if (s.isEmpty()) return true;
Stack<Character> res= new Stack<>();
for(Character c:s.toCharArray()){
if(c=='('){
res.push(')');
}else if(c=='{'){
res.push('}');
}else if(c=='['){
res.push(']');
}else if(res.empty()||res.pop()!=c){
return false;
}
}
return res.empty();
}
}
155. 最小栈
1.额外最小栈
class MinStack {
Stack<Integer> minS;
Stack<Integer> stack;
public MinStack() {
stack = new Stack<Integer>();
minS = new Stack<Integer>();
minS.push(Integer.MAX_VALUE);
}
public void push(int val) {
minS.push(Math.min(val,minS.peek()));
stack.push(val);
}
public void pop() {
stack.pop();
minS.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return minS.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(val);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.getMin();
*/
225. 用队列实现栈
难度简单446
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
注意:
- 你只能使用队列的基本操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。 - 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
两个栈交替添加元素
class MyStack {
Queue<Integer> q1;
Queue<Integer> q2;
public MyStack() {
this.q1=new LinkedList<>();
this.q2=new LinkedList<>();
}
public void push(int x) {
q2.add(x);
while(!q1.isEmpty()){
q2.add(q1.poll());
}
Queue<Integer> tem=q2;
q2=q1;
q1=tem;
}
public int pop() {
return q1.poll();
}
public int top() {
return q1.peek();
}
public boolean empty() {
return q1.isEmpty();
}
}
/**
* Your MyStack object will be instantiated and called as such:
* MyStack obj = new MyStack();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.top();
* boolean param_4 = obj.empty();
*/
单调栈:
单调栈总结
单调递增栈:从 栈底 到 栈顶 递增,栈顶大
单调递减栈:从 栈底 到 栈顶 递减,栈顶小
1:什么时候使用单调栈?
通常是一维数组,要寻找任一元素右边(左边)第一个比自己大(小)的元素,且要求 O(n) 的时间复杂度
2:模板套路
Deque<Integer> stack = new Stack<Integer>();
for(int i=temperatures.length-1;i>=0;i--){
while(!stack.empty()&&temperatures[stack.peek()]<=temperatures[i]){
stack.pop();
}
stack.push(i);
}
Deque<Integer> stack = new ArrayDeque<Integer>();
for (int i = nums2.length - 1; i >= 0; --i) {
int num = nums2[i];
while (!stack.isEmpty() && num >= stack.peek()) {
stack.pop();
}
stack.push(num);
}
1): 当前项向右找第一个比自己大的位置 —— 从右向左维护一个单调递减栈
2): 当前项向左找第一个比自己大的位置 —— 从左向右维护一个单调递减栈
反之也可
84. 柱状图中最大的矩形
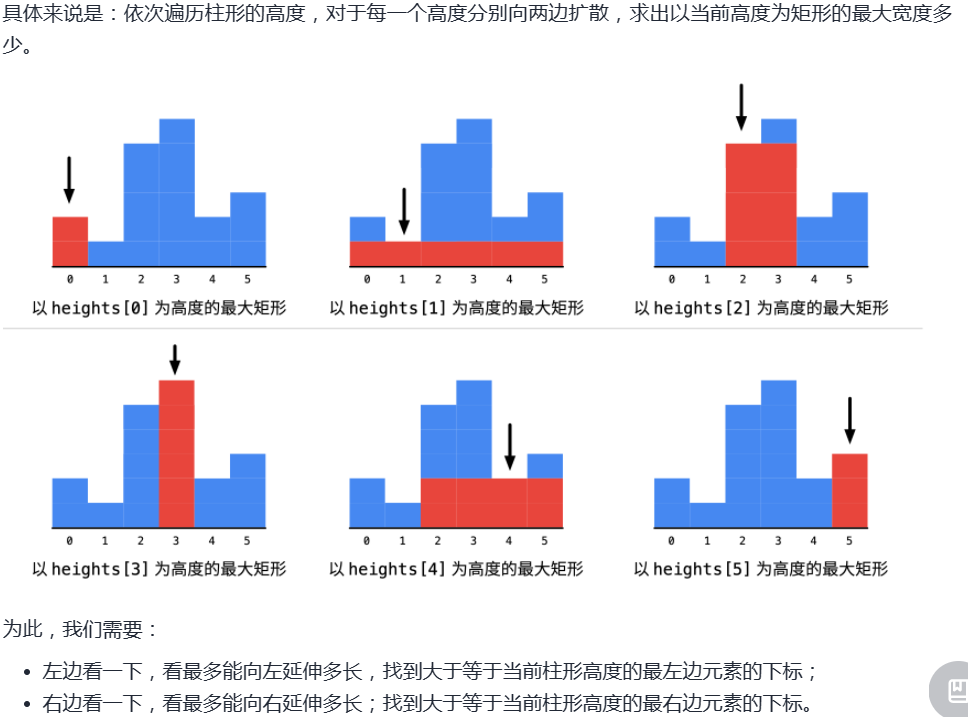
1.暴力法 超时
class Solution {
public int largestRectangleArea(int[] heights) {
int maxarea=0;
if(heights.length==1) return heights[0];
for(int i=0;i<heights.length;i++){
int left=i;
int right=i;
while(right<heights.length&&heights[right]>=heights[i]){
right++;
}
while(left>=0&&heights[left]>=heights[i]){
left--;
}
maxarea = Math.max(maxarea,heights[i]*(right-1-left));
}
return maxarea;
}
}
2.哨兵 单调栈
我们就拿示例的数组 [2, 1, 5, 6, 2, 3] 为例:


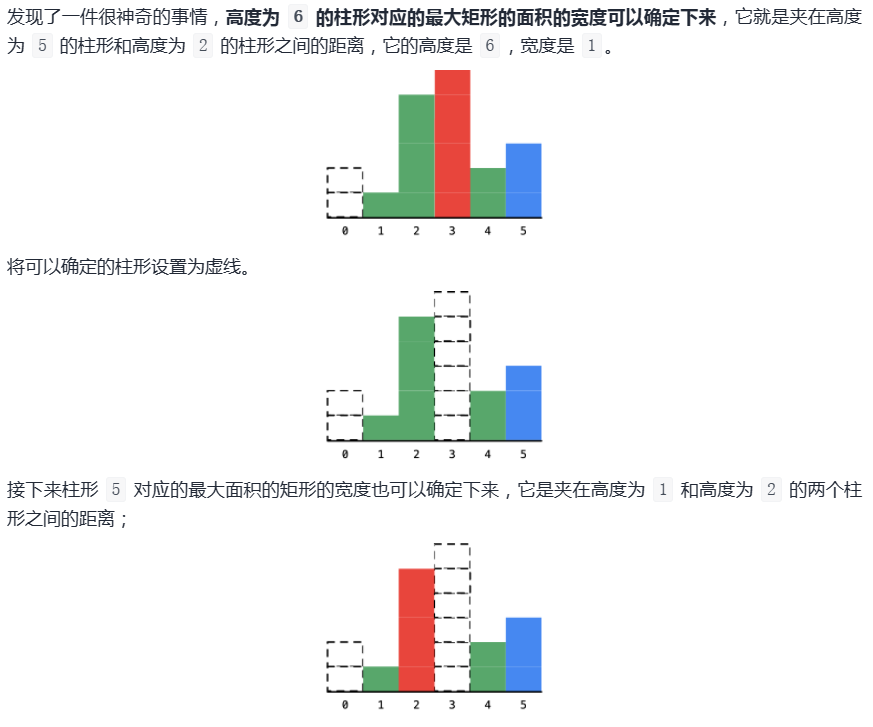
这里会有一种特殊情况。如果我们移除了栈中所有的 j值,那就说明 i 左侧所有柱子的高度都大于 height[i],那么我们可以认为 i 左侧且最近的小于其高度的柱子在位置 j=-1,它是一根「虚拟」的、高度无限低的柱子
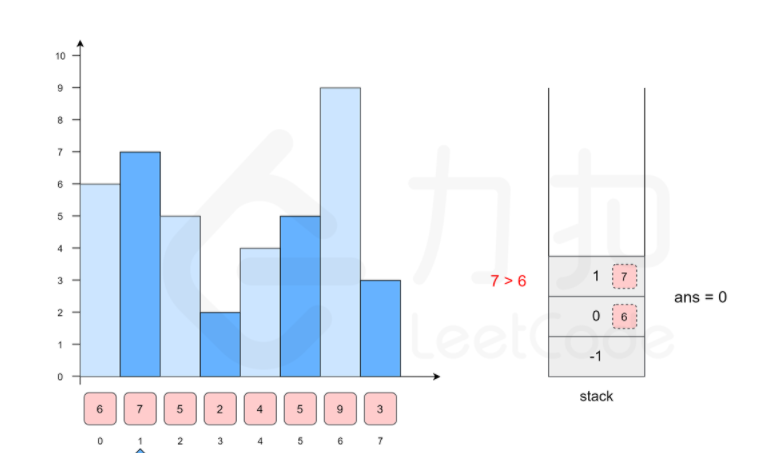
class Solution {
public int largestRectangleArea(int[] heights) {
int maxarea=0;
Stack<Integer> stack=new Stack<>();
stack.push(-1);
for(int i=0;i<heights.length;i++){
while(stack.peek()!=-1&&heights[stack.peek()]>=heights[i]){
maxarea=Math.max(maxarea,heights[stack.pop()]*(i-stack.peek()-1));
}
stack.push(i);
}
while(stack.peek()!=-1){
maxarea=Math.max(maxarea,heights[stack.pop()]*(heights.length-stack.peek()-1));
}
return maxarea;
}
}
739. 每日温度
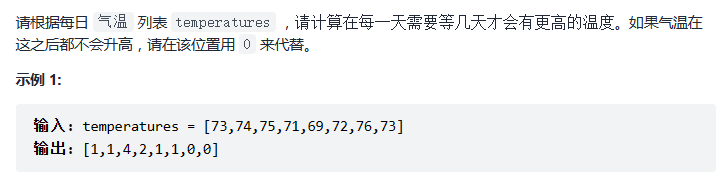
1.单调栈
反向遍历,维护一个储存下标的栈从栈底到栈顶的下标对应的温度列表中的温度依次递减(表示未来最近的温度较高的天),找到后面最接近的大于tempertures[i]的温度,如果找不到栈顶弹出。栈为空则证明后面没有比当前温度更高的天了,当前温度入栈ans[i]=0,
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int[] ans = new int[temperatures.length];
Stack<Integer> stack=new Stack<>();
// int count=0;
// int index=0;
ans[temperatures.length-1]=0;
for(int i=temperatures.length-1;i>=0;i--){
while(!stack.empty()&&temperatures[stack.peek()]<=temperatures[i]){
stack.pop();
// count--;
}
if(!stack.empty()){
ans[i]=stack.peek()-i;
}else{
ans[i]=0;
}
stack.push(i);
}
return ans;
}
}
正向遍历,可以维护一个存储下标的单调栈,从栈底到栈顶的下标对应的温度列表中的温度依次递减。如果一个下标在单调栈里,则表示尚未找到下一次温度更高的下标。 找到了就弹出
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int length = temperatures.length;
int[] ans = new int[length];
Deque<Integer> stack = new LinkedList<Integer>();
for (int i = 0; i < length; i++) {
int temperature = temperatures[i];
while (!stack.isEmpty() && temperature > temperatures[stack.peek()]) {
int prevIndex = stack.pop();
ans[prevIndex] = i - prevIndex;
}
stack.push(i);
}
return ans;
}
}
496. 下一个更大元素 I
给你两个 没有重复元素 的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。
请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。
示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于 num1 中的数字 4 ,你无法在第二个数组中找到下一个更大的数字,因此输出 -1 。
对于 num1 中的数字 1 ,第二个数组中数字1右边的下一个较大数字是 3 。
对于 num1 中的数字 2 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
正向遍历,单调栈
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
Deque<Integer> stack=new LinkedList<Integer>();
int[] ans=new int[nums1.length];
Map<Integer,Integer> map =new HashMap<Integer,Integer>();
for(int i=0;i<nums2.length;i++){
map.put(nums2[i],-1);
while(!stack.isEmpty()&&nums2[i]>stack.peek()){
map.put(stack.peek(),nums2[i]);
stack.pop();
}
stack.push(nums2[i]);
}
for(int i=0;i<nums1.length;i++){
ans[i]= map.get(nums1[i]);
}
return ans;
}
}
503. 下一个更大元素 II
中等
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
示例 1:
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2;
数字 2 找不到下一个更大的数;
第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
方法一:单调栈 + 循环数组
一个朴素的思想是,我们可以把这个循环数组「拉直」,即复制该序列的前 n-1n−1 个元素拼接在原序列的后面。这样我们就可以将这个新序列当作普通序列,用上文的方法来处理。
而在本题中,我们不需要显性地将该循环数组「拉直」,而只需要在处理时对下标取模即可。
class Solution {
public int[] nextGreaterElements(int[] nums) {
Deque<Integer> stack =new LinkedList<Integer>();
int n=nums.length;
int[] ans=new int[nums.length];
Arrays.fill(ans, -1);
for(int i=0;i<2*n-1;i++){
while(!stack.isEmpty()&&nums[i%nums.length]>nums[stack.peek()]){
ans[stack.pop()]=nums[i%nums.length];
}
stack.push(i%nums.length);
}
return ans;
}
}
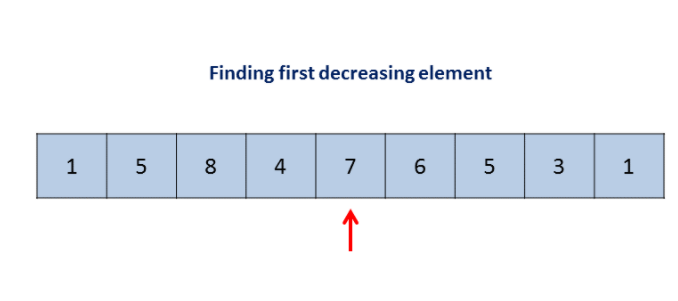
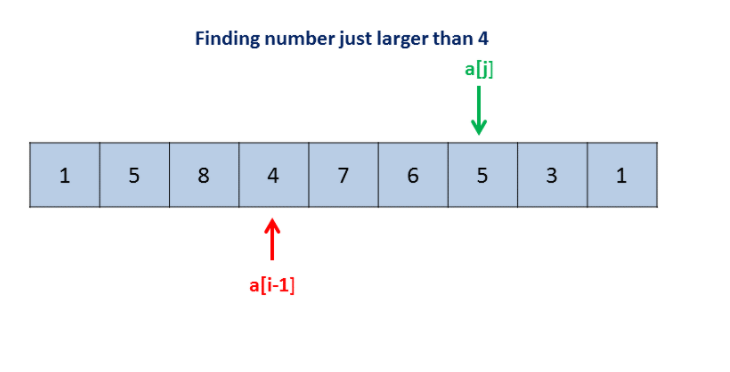
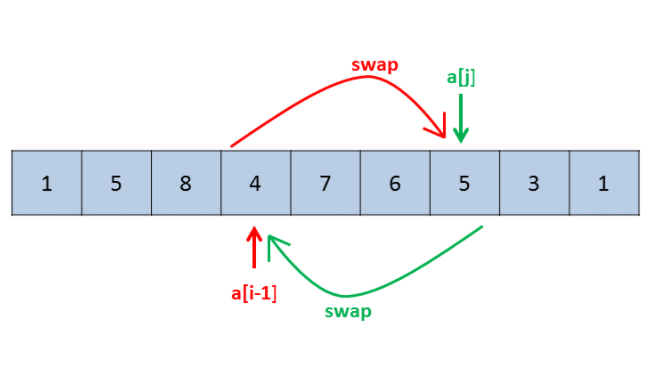
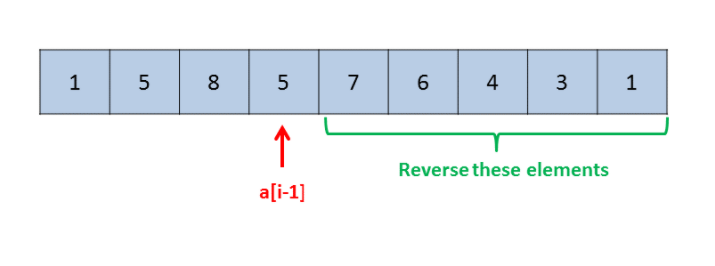
public class Solution {
public int nextGreaterElement(int n) {
char[] a = ("" + n).toCharArray();
int i = a.length - 2;
while (i >= 0 && a[i + 1] <= a[i]) {
i--;
}
if (i < 0)
return -1;
int j = a.length - 1;
while (j >= 0 && a[j] <= a[i]) {
j--;
}
swap(a, i, j);
reverse(a, i + 1);
try {
return Integer.parseInt(new String(a));
} catch (Exception e) {
return -1;
}
}
private void reverse(char[] a, int start) {
int i = start, j = a.length - 1;
while (i < j) {
swap(a, i, j);
i++;
j--;
}
}
private void swap(char[] a, int i, int j) {
char temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}



