刷题笔记3.数组、链表、跳表
数组、链表、跳表
- Java 源码分析(ArrayList)
- Linked List 的标准实现代码
- [Linked List 示例代码](http://www.cs.cmu.edu/~adamchik/15-121/lectures/Linked Lists/code/LinkedList.java)
- Java 源码分析(LinkedList)
- LRU Cache - Linked list: LRU 缓存机制
- Redis - Skip List:跳跃表、为啥 Redis 使用跳表(Skip List)而不是使用 Red-Black?
链表
JAVA:LinkedList 双向链表
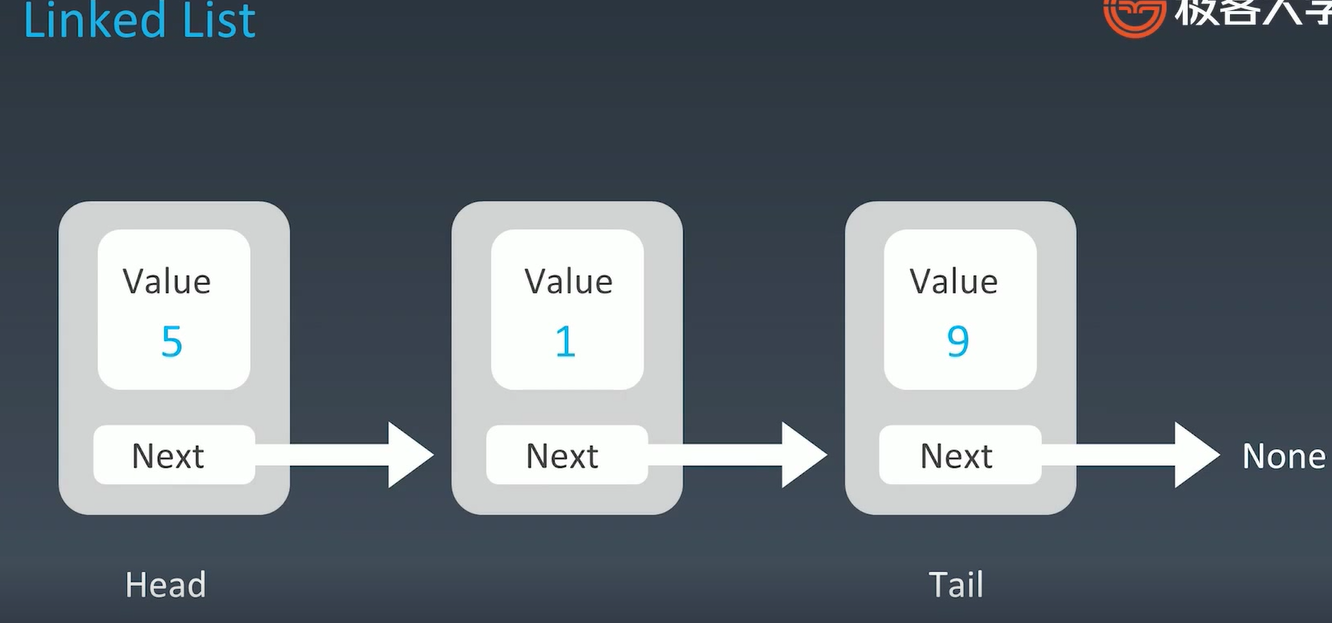
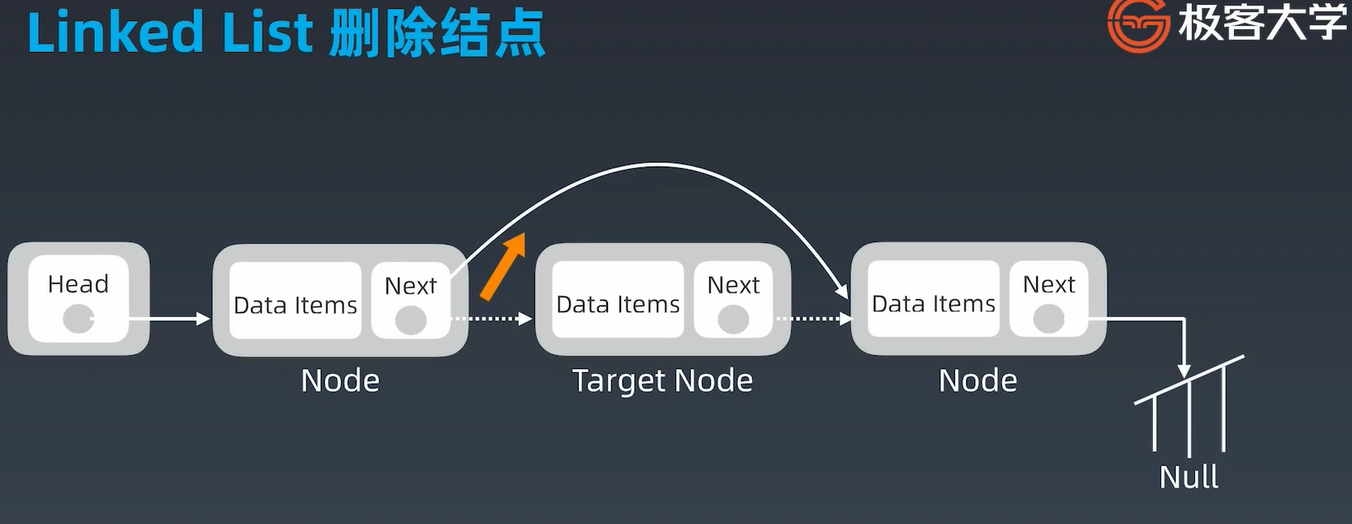
缺陷:lookup

数组时间复杂度:

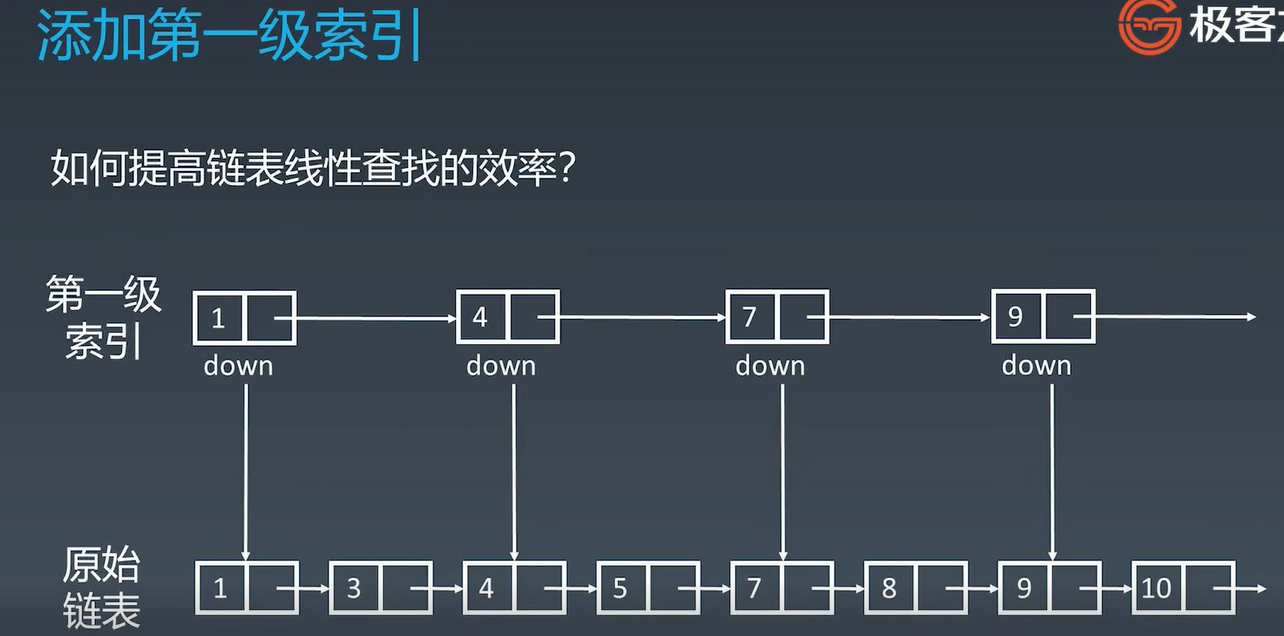
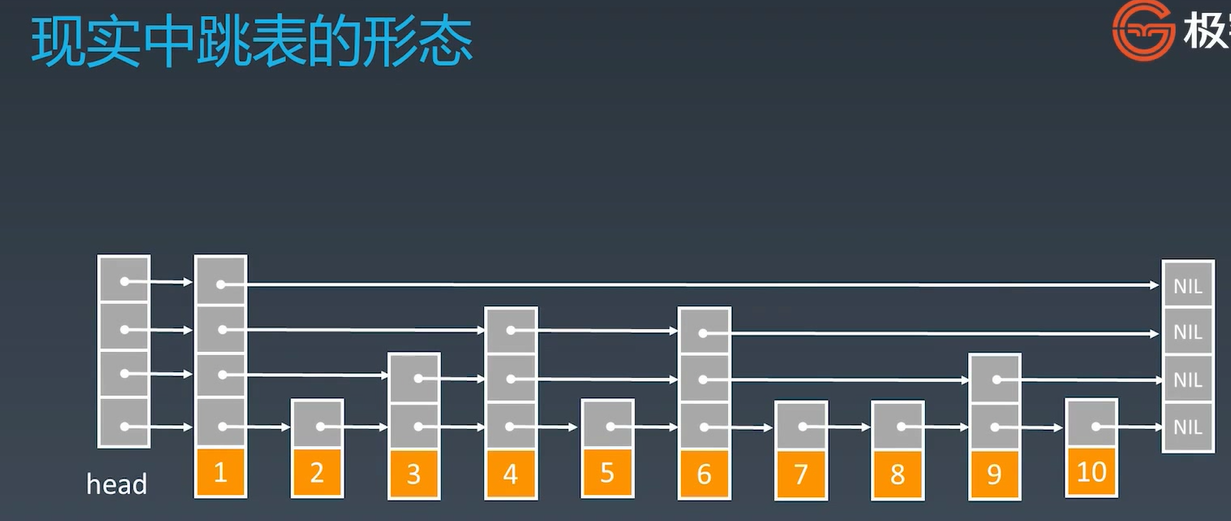
对链表查找进行优化:跳表(理解原理redis)
空间换时间、添加一级索引
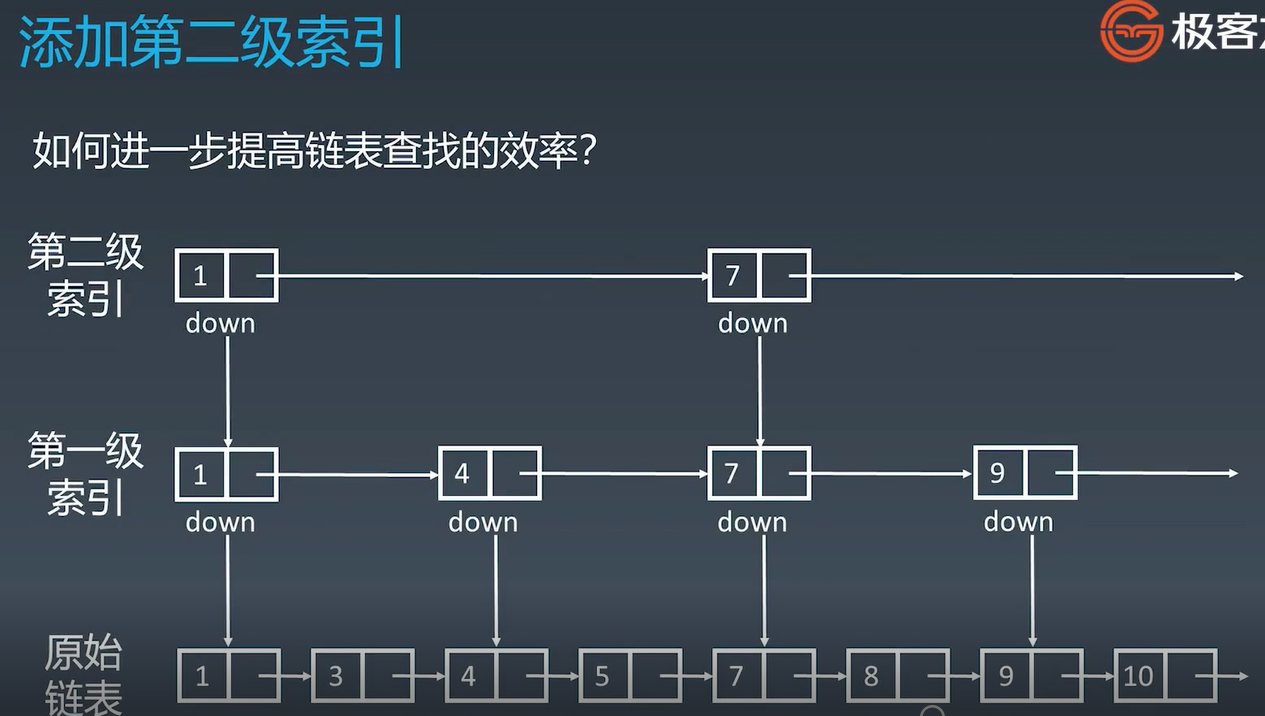
增加多级索引 log2n级

数组实战题目
283. 移动零
双指针
class Solution {
public void moveZeroes(int[] nums) {
int n=nums.length;
int j=0;
for(int i=0;i<n;i++){
if(nums[i]!=0){
nums[j]=nums[i];
if(i!=j){
nums[i]=0;
}
j++;
}
}
}
}
- 遍历数组,无为0的元素移动数组前方,用index下标记录。
- 遍历结束,对index值后的元素统一设为0
class Solution {
public void moveZeroes(int[] nums) {
int index = 0;
for(int num:nums){
if(num!=0){
nums[index++]=num;
}
}
while(index<nums.length){
nums[index++] = 0;
}
}
}
42. 接雨水
难度困难2847收藏分享切换为英文接收动态反馈
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
1.按列求雨水
找到此列 左右两边最大最高的列
- 较矮的墙的高度大于当前列的墙的高度
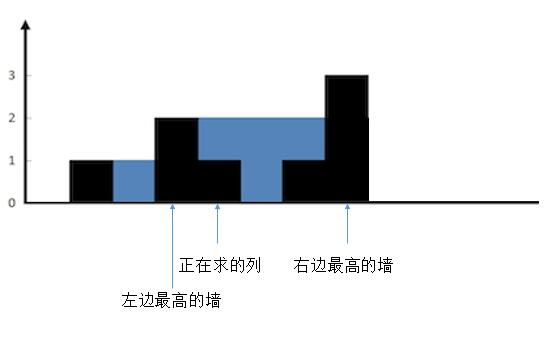
把正在求的列左边最高的墙和右边最高的墙确定后,然后为了方便理解,我们把无关的墙去掉。
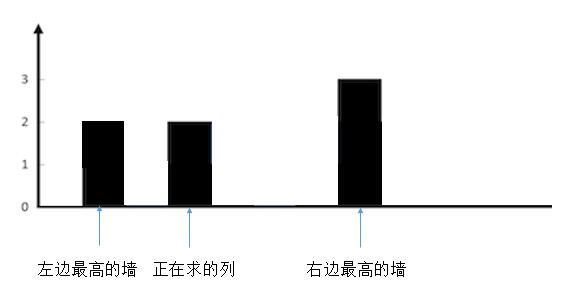
遍历每一列,然后分别求出这一列两边最高的墙。找出较矮的一端,和当前列的高度比较,结果就是上边的三种情况。
public int trap(int[] height) {
int sum = 0;
//最两端的列不用考虑,因为一定不会有水。所以下标从 1 到 length - 2
for (int i = 1; i < height.length - 1; i++) {
int max_left = 0;
//找出左边最高
for (int j = i - 1; j >= 0; j--) {
if (height[j] > max_left) {
max_left = height[j];
}
}
int max_right = 0;
//找出右边最高
for (int j = i + 1; j < height.length; j++) {
if (height[j] > max_right) {
max_right = height[j];
}
}
//找出两端较小的
int min = Math.min(max_left, max_right);
//只有较小的一段大于当前列的高度才会有水,其他情况不会有水
if (min > height[i]) {
sum = sum + (min - height[i]);
}
}
return sum;
}
2.动态规划
我们注意到,解法二中。对于每一列,我们求它左边最高的墙和右边最高的墙,都是重新遍历一遍所有高度,这里我们可以优化一下。
首先用两个数组,max_left [i] 代表第 i 列左边最高的墙的高度,max_right[i] 代表第 i 列右边最高的墙的高度。(一定要注意下,第 i 列左(右)边最高的墙,是不包括自身的,和 leetcode 上边的讲的有些不同)
max_left [i] = Max(max_left [i-1],height[i-1])。它前边的墙的左边的最高高度和它前边的墙的高度选一个较大的,就是当前列左边最高的墙了。
max_right[i] = Max(max_right[i+1],height[i+1]) 。它后边的墙的右边的最高高度和它后边的墙的高度选一个较大的,就是当前列右边最高的墙了。
3.双指针
例如这道题中,可以看到,max_left [ i ] 和 max_right [ i ] 数组中的元素我们其实只用一次,然后就再也不会用到了。所以我们可以不用数组,只用一个元素就行了。我们先改造下 max_left。
public int trap(int[] height) {
int sum = 0;
int max_left = 0;
int[] max_right = new int[height.length];
for (int i = height.length - 2; i >= 0; i--) {
max_right[i] = Math.max(max_right[i + 1], height[i + 1]);
}
for (int i = 1; i < height.length - 1; i++) {
max_left = Math.max(max_left, height[i - 1]);
int min = Math.min(max_left, max_right[i]);
if (min > height[i]) {
sum = sum + (min - height[i]);
}
}
return sum;
}
我们成功将 max_left 数组去掉了。但是会发现我们不能同时把 max_right 的数组去掉,因为最后的 for 循环是从左到右遍历的,而 max_right 的更新是从右向左的。
所以这里要用到两个指针,left 和 right,从两个方向去遍历。
那么什么时候从左到右,什么时候从右到左呢?根据下边的代码的更新规则,我们可以知道
max_left = Math.max(max_left, height[i - 1]);
height [ left - 1] 是可能成为 max_left 的变量, 同理,height [ right + 1 ] 是可能成为 right_max 的变量。
只要保证 height [ left - 1 ] < height [ right + 1 ] ,那么 max_left 就一定小于 max_right。
因为 max_left 是由 height [ left - 1] 更新过来的,而 height [ left - 1 ] 是小于 height [ right + 1] 的,而 height [ right + 1 ] 会更新 max_right,所以间接的得出 max_left 一定小于 max_right。
反之,我们就从右到左更。
public int trap(int[] height) {
int sum = 0;
int max_left = 0;
int max_right = 0;
int left = 1;
int right = height.length - 2; // 加右指针进去
for (int i = 1; i < height.length - 1; i++) {
//从左到右更
if (height[left - 1] < height[right + 1]) {
max_left = Math.max(max_left, height[left - 1]);
int min = max_left;
if (min > height[left]) {
sum = sum + (min - height[left]);
}
left++;
//从右到左更
} else {
max_right = Math.max(max_right, height[right + 1]);
int min = max_right;
if (min > height[right]) {
sum = sum + (min - height[right]);
}
right--;
}
}
return sum;
}
class Solution {
public int trap(int[] height) {
int ans = 0;
int left = 0, right = height.length - 1;
int leftMax = 0, rightMax = 0;
while (left < right) {
leftMax = Math.max(leftMax, height[left]);
rightMax = Math.max(rightMax, height[right]);
if (height[left] < height[right]) {
ans += leftMax - height[left];
++left;
} else {
ans += rightMax - height[right];
--right;
}
}
return ans;
}
}
4 单调栈
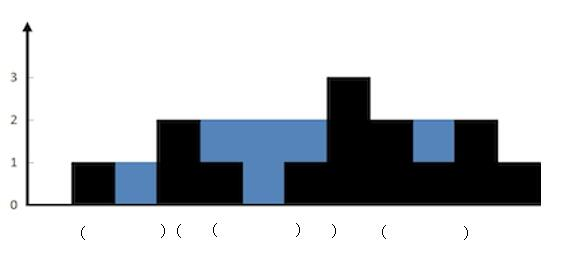
说到栈,我们肯定会想到括号匹配了。我们仔细观察蓝色的部分,可以和括号匹配类比下。每次匹配出一对括号(找到对应的一堵墙),就计算这两堵墙中的水。
总体的原则就是,
-
当前高度小于等于栈顶高度,入栈,指针后移。
-
当前高度大于栈顶高度,出栈,计算出当前墙和栈顶的墙之间水的多少,然后计算当前的高度和新栈的高度的关系,重复第 2 步。直到当前墙的高度不大于栈顶高度或者栈空,然后把当前墙入栈,指针后移。
我们看具体的例子。
首先将 height [ 0 ] 入栈。然后 current 指向的高度大于栈顶高度,所以把栈顶 height [ 0 ] 出栈,然后栈空了,再把 height [ 1 ] 入栈。current 后移。
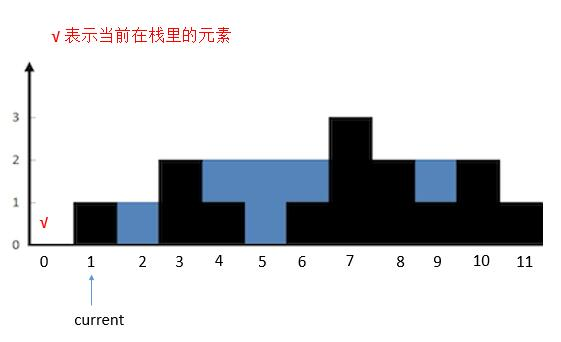
- 然后
current指向的高度小于栈顶高度,height [ 2 ]入栈,current后移。
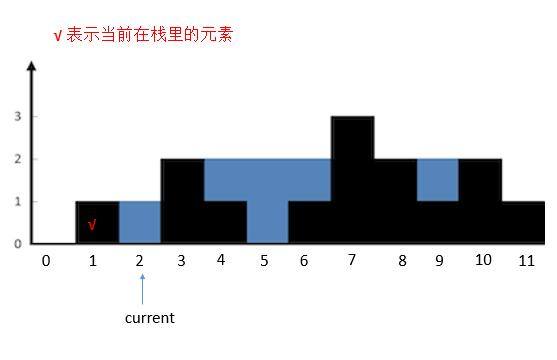
然后 current 指向的高度大于栈顶高度,栈顶 height [ 2 ] 出栈。计算 height [ 3 ] 和新的栈顶之间的水。计算完之后继续判断 current 和新的栈顶的关系。
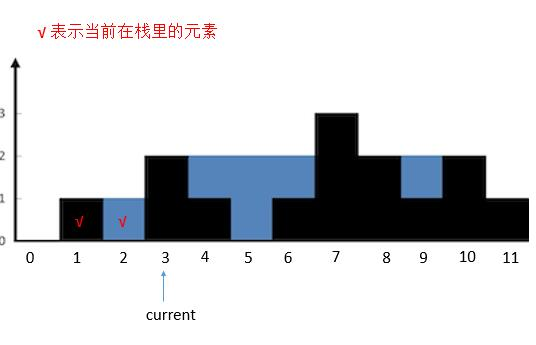
current指向的高度大于栈顶高度,栈顶height [ 1 ]出栈,栈空。所以把height [ 3 ]入栈。currtent后移。
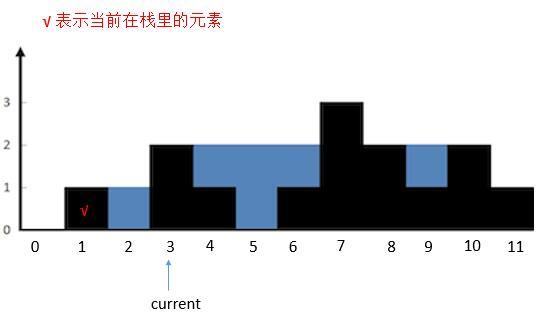
- 然后
current指向的高度小于栈顶height [ 3 ]的高度,height[ 4 ]入栈。current后移。
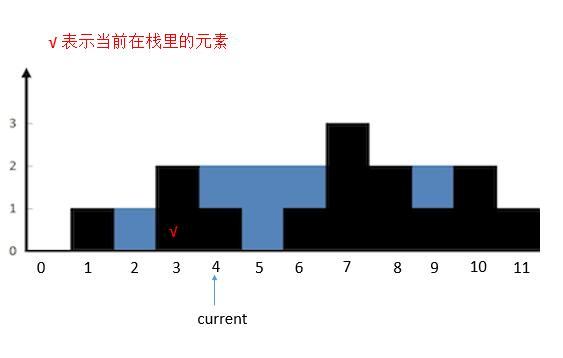
- 然后
current指向的高度小于栈顶height [ 4 ]的高度,height [ 5 ]入栈。current后移。
然后 current 指向的高度大于栈顶 height [ 5 ] 的高度,将栈顶 height [ 5 ] 出栈,然后计算 current 指向的墙和新栈顶 height [ 4 ] 之间的水。计算完之后继续判断 current 的指向和新栈顶的关系。此时 height [ 6 ] 不大于栈顶 height [ 4 ] ,所以将 height [ 6 ] 入栈。current 后移。



public int trap6(int[] height) {
int sum = 0;
Stack<Integer> stack = new Stack<>();
int current = 0;
while (current < height.length) {
//如果栈不空并且当前指向的高度大于栈顶高度就一直循环
while (!stack.empty() && height[current] > height[stack.peek()]) {
int h = height[stack.peek()]; //取出要出栈的元素
stack.pop(); //出栈
if (stack.empty()) { // 栈空就出去
break;
}
int distance = current - stack.peek() - 1; //两堵墙之前的距离。
int min = Math.min(height[stack.peek()], height[current]);
sum = sum + distance * (min - h);
}
stack.push(current); //当前指向的墙入栈
current++; //指针后移
}
return sum;
}
11. 盛最多水的容器
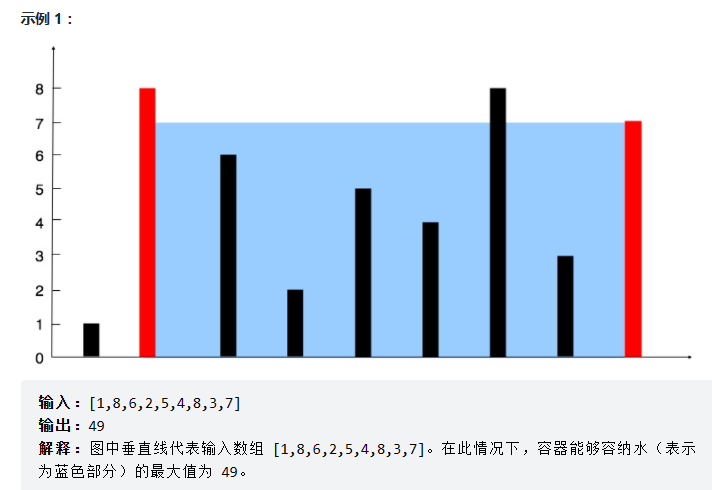
双指针
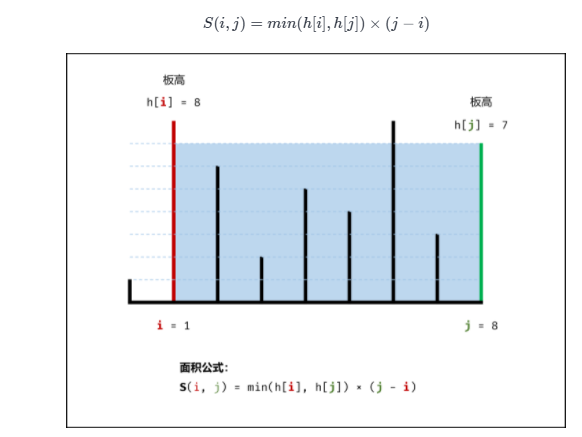
在每个状态下,无论长板或短板向中间收窄一格,都会导致水槽 底边宽度 -1 变短:
若向内 移动短板 ,水槽的短板 min(h[i], h[j]) 可能变大,因此下个水槽的面积 可能增大 。
若向内 移动长板 ,水槽的短板 min(h[i], h[j]) 不变或变小,因此下个水槽的面积 一定变小
因此,初始化双指针分列水槽左右两端,循环每轮将短板向内移动一格,并更新面积最大值,直到两指针相遇时跳出;即可获得最大面积。
public class Solution {
public int maxArea(int[] height) {
int l = 0, r = height.length - 1;
int ans = 0;
while (l < r) {
int area = Math.min(height[l], height[r]) * (r - l);
ans = Math.max(ans, area);
if (height[l] <= height[r]) {
++l;
}
else {
--r;
}
}
return ans;
}
}
70. 爬楼梯
dp[i]=dp[i-1]+dp[i-2];
class Solution {
public int climbStairs(int n) {
int[] dp=new int[n+1];
dp[0]=1;
dp[1]=1;
if(n<=1){
return dp[n];
}
for(int i=2;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
}
15. 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
排序+双指针
- 首先对数组进行排序,排序后固定一个数 nums[i],再使用左右指针指向 nums[i]后面的两端,数字分别为 nums[L] 和 nums[R],计算三个数的和 sumsum 判断是否满足为 00,满足则添加进结果集
- 如果 nums[i]大于 0,则三数之和必然无法等于 0,结束循环
- 如果 nums[i] == nums[i-1],则说明该数字重复,会导致结果重复,所以应该跳过
- 当 sum == 0 时,nums[L]== nums[L+1 则会导致结果重复,应该跳过,L++
- 当 sum== 0 时,nums[R]== nums[R-1]则会导致结果重复,应该跳过,R--
- 时间复杂度:O(n^2)O,nn 为数组长度
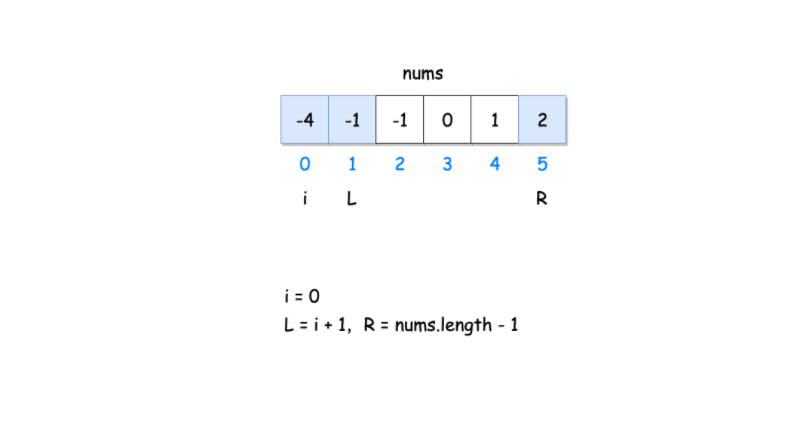

class Solution {
public static List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> ans = new ArrayList();
int len = nums.length;
if(nums == null || len < 3) return ans;
Arrays.sort(nums); // 排序
for (int i = 0; i < len ; i++) {
if(nums[i] > 0) break; // 如果当前数字大于0,则三数之和一定大于0,所以结束循环
if(i > 0 && nums[i] == nums[i-1]) continue; // 去重
int L = i+1;
int R = len-1;
while(L < R){
int sum = nums[i] + nums[L] + nums[R];
if(sum == 0){
ans.add(Arrays.asList(nums[i],nums[L],nums[R]));
while (L<R && nums[L] == nums[L+1]) L++; // 去重
while (L<R && nums[R] == nums[R-1]) R--; // 去重
L++;
R--;
}
else if (sum < 0) L++;
else if (sum > 0) R--;
}
}
return ans;
}
}
up-16. 最接近的三数之和
难度中等996收藏分享切换为英文接收动态反馈
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。
示例 1:
输入:nums = [-1,2,1,-4], target = 1
输出:2
解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
class Solution {
public int threeSumClosest(int[] nums, int target) {
Arrays.sort(nums);
int best=1000000//不能用MAXVLUE,减去target可能会溢出
for(int i=0;i<nums.length;i++){
if(i>0&&nums[i]==nums[i-1]) continue;
int left=i+1;
int right=nums.length-1;
while(left<right){
int sum=nums[left]+nums[right]+nums[i];
if(sum==target) return sum;
if (Math.abs(sum - target) < Math.abs(best - target)) {
best = sum;
}
if(sum>target){
//右边找到下一个不相等的数
right--;
while(left<right&&nums[right]==nums[right+1]){
right--;
}
}else{
//左边找到下一个不相等的数
left++;
while(left<right&&nums[left]==nums[left-1]){
left++;
}
}
}
}
return best;
}
}
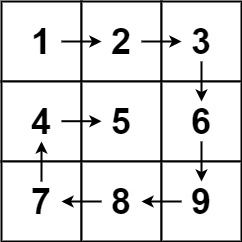
54. 螺旋矩阵
难度中等955收藏分享切换为英文接收动态反馈
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
int m=matrix.length,n=matrix[0].length;
int right=n-1,bottom=m-1,left=0,top=0;
int x=0,y=0;
List<Integer> res=new ArrayList<>();
while(true){
for(int i=left;i<=right;i++){
res.add(matrix[top][i]);
}
if(++top>bottom) break;
for(int i=top;i<=bottom;i++){
res.add(matrix[i][right]);
}
if(--right<left) break;
for(int i=right;i>=left;i--){
res.add(matrix[bottom][i]);
}
if(--bottom<top) break;
for(int i=bottom;i>=top;i--){
res.add(matrix[i][left]);
}
if(++left>right) break;
}
return res;
}
}
链表实战题目
206. 反转链表
1.双指针
class Solution {
public ListNode reverseList(ListNode head) {
if(head==null) return null;
ListNode node1= head;
ListNode node2= head.next;
node1.next=null;
while(node2!=null){
ListNode temp =node2.next;
node2.next=node1;
node1=node2;
node2=temp;
}
return node1;
}
}
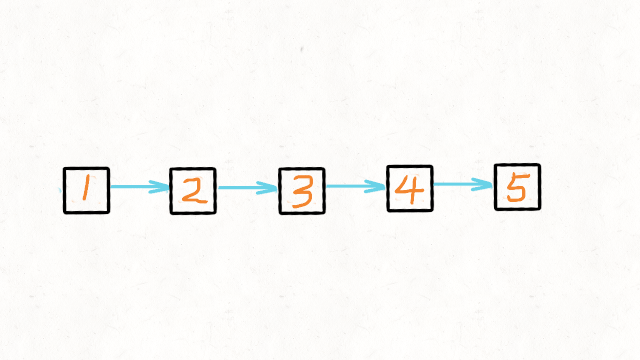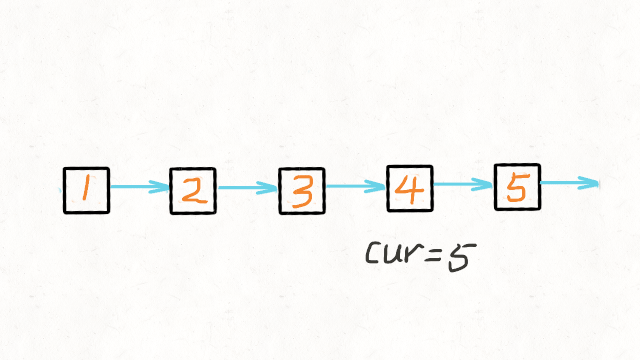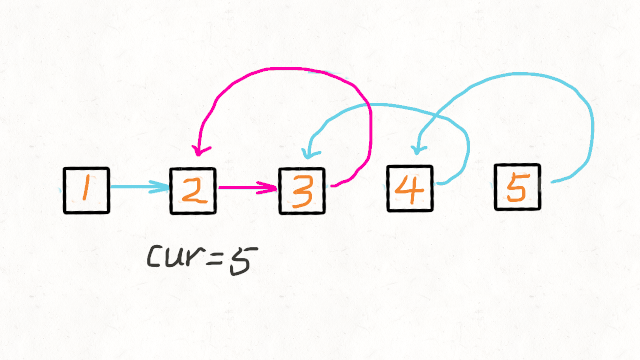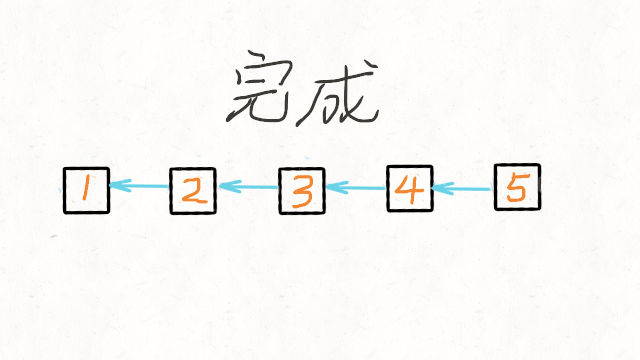
2.简洁的递归
使用递归函数,一直递归到链表的最后一个结点,该结点就是反转后的头结点,记作 retret .
此后,每次函数在返回的过程中,让当前结点的下一个结点的 next 指针指向当前节点。
同时让当前结点的 next指针指向 NULL ,从而实现从链表尾部开始的局部反转
当递归函数全部出栈后,链表反转完成。
动画演示如下:

class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode p = reverseList(head.next);
head.next.next = head;
head.next = null;
return p;
}
}
92. 反转链表 II
难度中等1115收藏分享切换为英文接收动态反馈
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
示例 1:
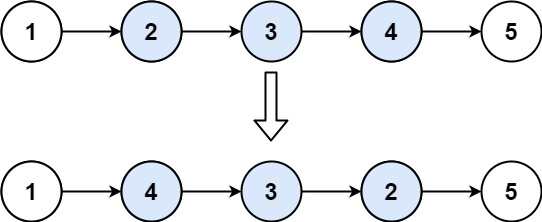
输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
头插法
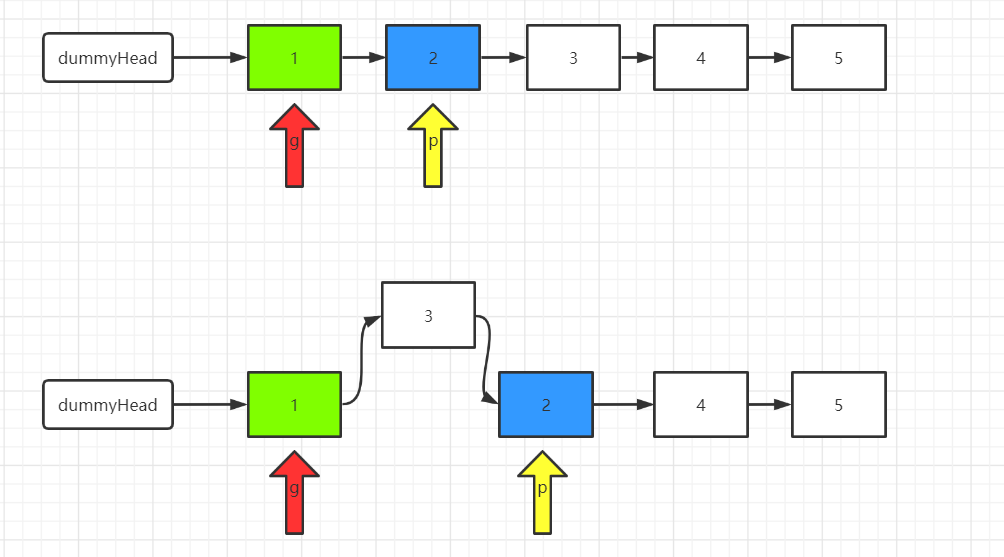
class Solution {
public ListNode reverseBetween(ListNode head, int m, int n) {
// 定义一个dummyHead, 方便处理
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
// 初始化指针
ListNode g = dummyHead;
ListNode p = dummyHead.next;
// 将指针移到相应的位置
for(int step = 0; step < m - 1; step++) {
g = g.next; p = p.next;
}
// 头插法插入节点
for (int i = 0; i < n - m; i++) {
ListNode removed = p.next;
p.next = p.next.next;
removed.next = g.next;
g.next = removed;
}
return dummyHead.next;
}
}
24. 两两交换链表中的节点
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换
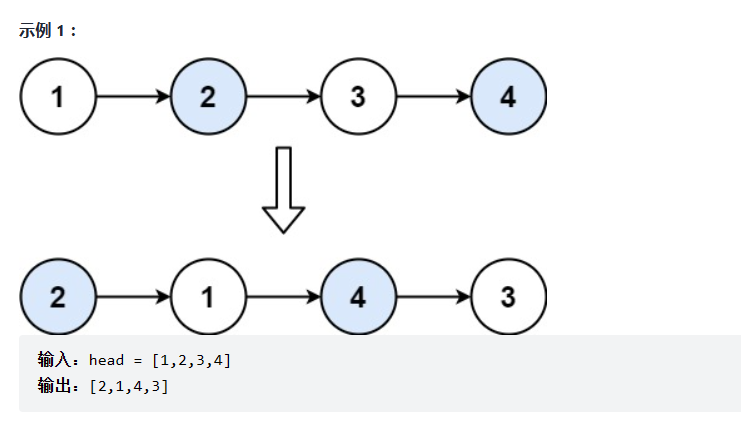
1.不加虚拟头节点
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode swapPairs(ListNode head) {
if(head==null) return null;
if(head.next==null) return head;
ListNode cur=head.next;
ListNode pre=head;
ListNode temp =cur.next;
pre.next=cur.next;
cur.next=pre;
head = cur;
while(temp!=null&&temp.next!=null){
cur=temp.next;
pre.next=cur;
pre=temp;
temp =cur.next;
pre.next=cur.next;
cur.next=pre;
}
return head;
}
}
2.加上虚拟头节点
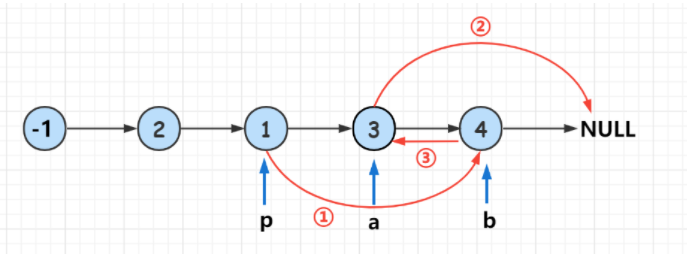
class Solution {
public ListNode swapPairs(ListNode head) {
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
ListNode temp = dummyHead;
while (temp.next != null && temp.next.next != null) {
ListNode node1 = temp.next;
ListNode node2 = temp.next.next;
temp.next = node2;
node1.next = node2.next;
node2.next = node1;
temp = node1;
}
return dummyHead.next;
}
}
3递归
class Solution {
public ListNode swapPairs(ListNode head) {
if(head==null||head.next==null) return head;
ListNode newHead=head.next;
head.next=swapPairs(newHead.next);
newHead.next=head;
return newHead;
}
}
141. 环形链表
1.哈希表
思路及算法
最容易想到的方法是遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
具体地,我们可以使用哈希表来存储所有已经访问过的节点。每次我们到达一个节点,如果该节点已经存在于哈希表中,则说明该链表是环形链表,否则就将该节点加入哈希表中。重复这一过程,直到我们遍历完整个链表即可
public class Solution {
public boolean hasCycle(ListNode head) {
Set<ListNode> seen = new HashSet<ListNode>();
while (head != null) {
if (!seen.add(head)) {
return true;
}
head = head.next;
}
return false;
}
}
快慢指针
slow,fast
假想「乌龟」和「兔子」在链表上移动,「兔子」跑得快,「乌龟」跑得慢。当「乌龟」和「兔子」从链表上的同一个节点开始移动时,如果该链表中没有环,那么「兔子」将一直处于「乌龟」的前方;如果该链表中有环,那么「兔子」会先于「乌龟」进入环,并且一直在环内移动。等到「乌龟」进入环时,由于「兔子」的速度快,它一定会在某个时刻与乌龟相遇,即套了「乌龟」若干圈
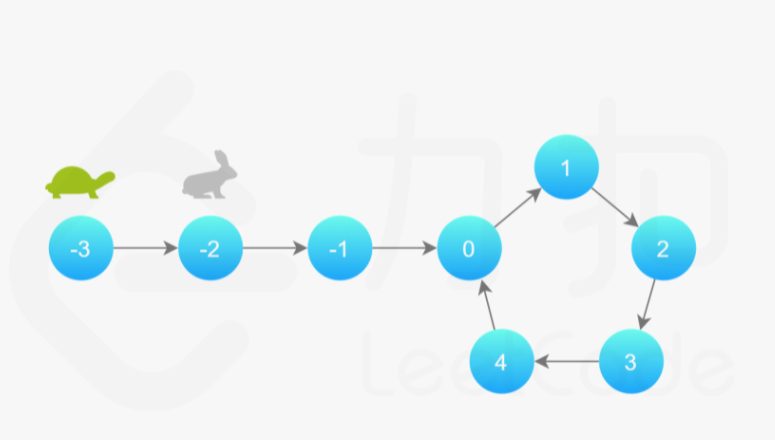
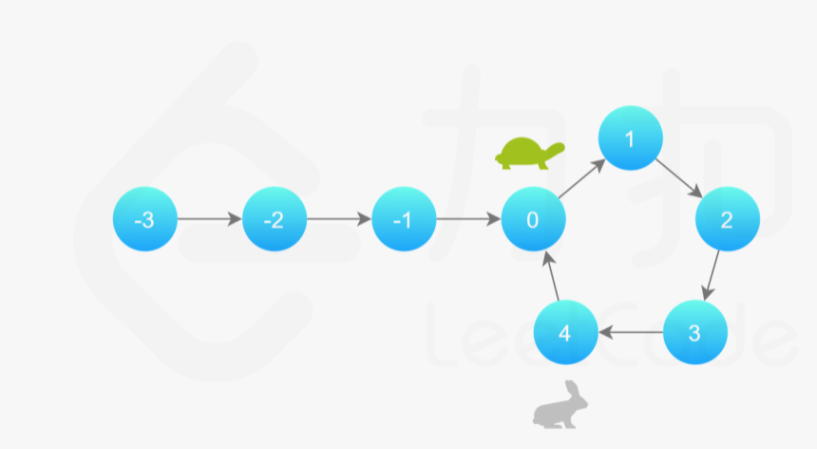
public class Solution {
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) {
return false;
}
ListNode slow = head;
ListNode fast = head.next;
while (slow != fast) {
if (fast == null || fast.next == null) {
return false;
}
slow = slow.next;
fast = fast.next.next;
}
return true;
}
}
142. 环形链表 II
方法一:哈希表
思路与算法
一个非常直观的思路是:我们遍历链表中的每个节点,并将它记录下来;一旦遇到了此前遍历过的节点,就可以判定链表中存在环。借助哈希表可以很方便地实现。
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode pos = head;
Set<ListNode> visited = new HashSet<ListNode>();
while (pos != null) {
if (visited.contains(pos)) {
return pos;
} else {
visited.add(pos);
}
pos = pos.next;
}
return null;
}
}
方法二:双指针
这类链表题目一般都是使用双指针法解决的,例如寻找距离尾部第K个节点、寻找环入口、寻找公共尾部入口等
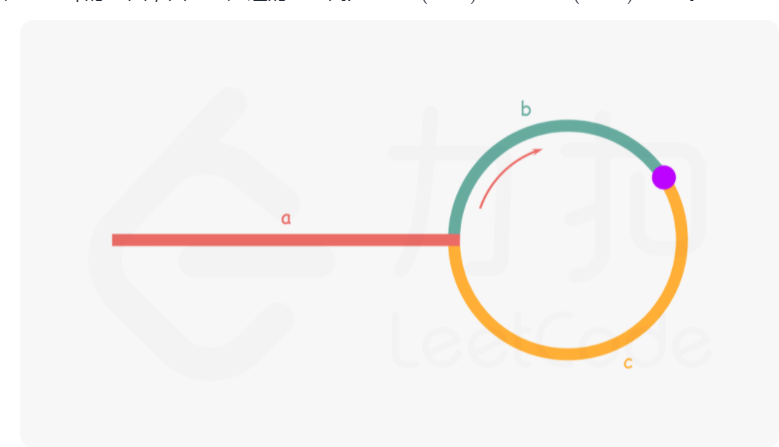
设链表共有 a+b个节点
双指针第一次相遇: 设两指针 fast,slow 指向链表头部 head,fast 每轮走 2 步,slow 每轮走 1 步
第一种结果: fast 指针走过链表末端,说明链表无环,直接返回 null;
TIPS: 若有环,两指针一定会相遇。因为每走 1 轮,fast 与 slow 的间距 +1,fast 终会追上 slow
第二种结果: 当fast == slow时, 两指针在环中 第一次相遇 。下面分析此时fast 与 slow走过的 步数关系 :
fast走的步数是slow步数的 22 倍,即 f = 2sf=2s;(解析:fast每轮走 22 步)fast比slow多走了 nn 个环的长度,即 f = s + nb;- 以上两式相减得:f = 2nb,s = nb,即
fast和slow指针分别走了 2n,n 个 环的周长
如果让指针从链表头部一直向前走并统计步数k,那么所有 走到链表入口节点时的步数 是:k=a+nb,此时只需要让slow再走a步就能到达入口,所以一个新的指针从head开始能和slow同时再走a步到达入口
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
if(head==null) return null;
ListNode slow=head;
ListNode fast=head;
while(true){
if(fast==null||fast.next==null) return null;
slow=slow.next;
fast=fast.next.next;
if(fast==slow) break;
}
ListNode temp=head;
while(slow!=temp){
slow=slow.next;
temp=temp.next;
}
return slow;
}
}
25. K 个一组翻转链表
难度困难
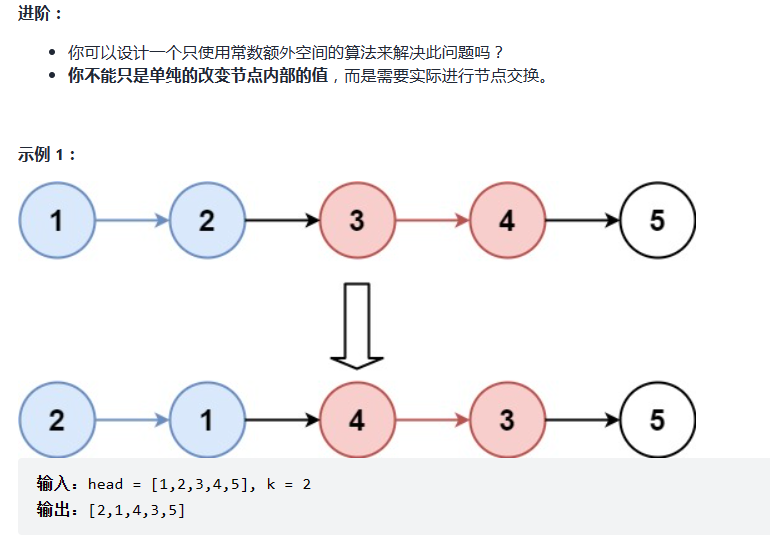
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
步骤分解:
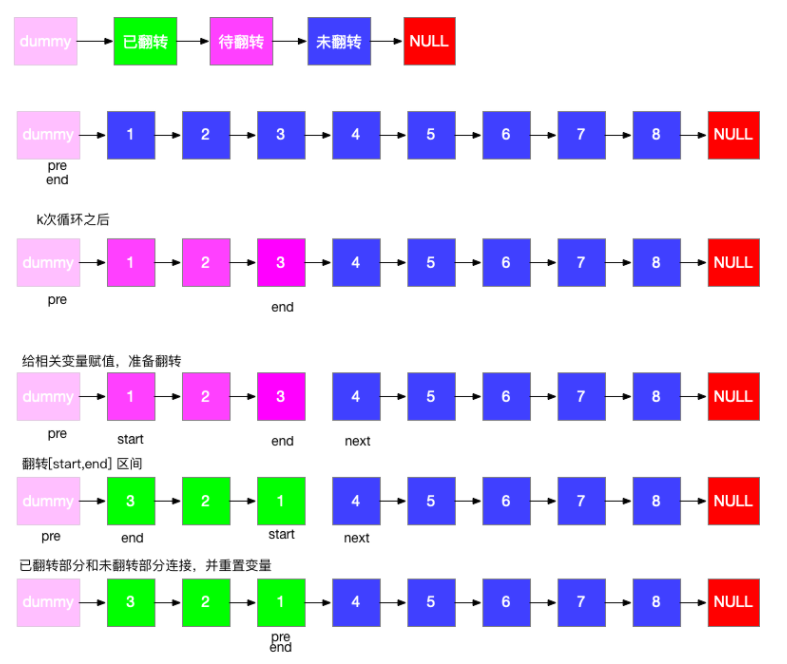
- 链表分区为已翻转部分+待翻转部分+未翻转部分
- 每次翻转前,要确定翻转链表的范围,这个必须通过 k 此循环来确定
- 需记录翻转链表前驱和后继,方便翻转完成后把已翻转部分和未翻转部分连接起来
- 初始需要两个变量 pre 和 end,pre 代表待翻转链表的前驱,end 代表待翻转链表的末尾
- 经过k此循环,end 到达末尾,记录待翻转链表的后继 next = end.next
- 翻转链表,然后将三部分链表连接起来,然后重置 pre 和 end 指针,然后进入下一次循环
- 特殊情况,当翻转部分长度不足 k 时,在定位 end 完成后,end==null,已经到达末尾,说明题目已完成,直接返回即可
- 时间复杂度为 O(n*K)O(n∗K) 最好的情况为 O(n)O(n) 最差的情况未 O(n^2)
- 空间复杂度为 O(1)O(1) 除了几个必须的节点指针外,我们并没有占用其他空间

class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
if (head == null || head.next == null){
return head;
}
//定义一个假的节点。
ListNode dummy=new ListNode(0);
//假节点的next指向head。
// dummy->1->2->3->4->5
dummy.next=head;
//初始化pre和end都指向dummy。pre指每次要翻转的链表的头结点的上一个节点。end指每次要翻转的链表的尾节点
ListNode pre=dummy;
ListNode end=dummy;
while(end.next!=null){
//循环k次,找到需要翻转的链表的结尾,这里每次循环要判断end是否等于空,因为如果为空,end.next会报空指针异常。
//dummy->1->2->3->4->5 若k为2,循环2次,end指向2
for(int i=0;i<k&&end != null;i++){
end=end.next;
}
//如果end==null,即需要翻转的链表的节点数小于k,不执行翻转。
if(end==null){
break;
}
//先记录下end.next,方便后面链接链表
ListNode next=end.next;
//然后断开链表
end.next=null;
//记录下要翻转链表的头节点
ListNode start=pre.next;
//翻转链表,pre.next指向翻转后的链表。1->2 变成2->1。 dummy->2->1
pre.next=reverse(start);
//翻转后头节点变到最后。通过.next把断开的链表重新链接。
start.next=next;
//将pre换成下次要翻转的链表的头结点的上一个节点。即start
pre=start;
//翻转结束,将end置为下次要翻转的链表的头结点的上一个节点。即start
end=start;
}
return dummy.next;
}
//链表翻转
// 例子: head: 1->2->3->4
public ListNode reverse(ListNode head) {
//单链表为空或只有一个节点,直接返回原单链表
if (head == null || head.next == null){
return head;
}
//前一个节点指针
ListNode preNode = null;
//当前节点指针
ListNode curNode = head;
//下一个节点指针
ListNode nextNode = null;
while (curNode != null){
nextNode = curNode.next;//nextNode 指向下一个节点,保存当前节点后面的链表。
curNode.next=preNode;//将当前节点next域指向前一个节点 null<-1<-2<-3<-4
preNode = curNode;//preNode 指针向后移动。preNode指向当前节点。
curNode = nextNode;//curNode指针向后移动。下一个节点变成当前节点
}
return preNode;
}
}
143. 重排链表
难度中等752收藏分享切换为英文接收动态反馈
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
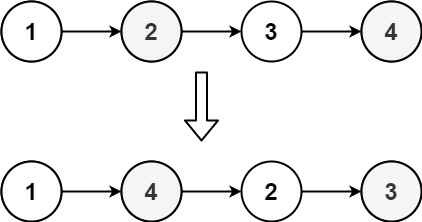
输入:head = [1,2,3,4]
输出:[1,4,2,3]
快慢指针+反转链表+合并链表
public void reorderList(ListNode head) {
if (head == null) {
return;
}
// 获得中间节点
ListNode mid = findMid(head);
// 中间节点之后的部分进行反转
ListNode head2 = mid.next;
mid.next = null;
head2 = reverseList(head2);
// 合并
ListNode head1 = head;
mergeList(head1, head2);
}
// LeetCode 876
private ListNode findMid(ListNode head){
ListNode slow = head;
ListNode fast = head;
while (fast.next != null && fast.next.next != null) {
slow = slow.next;
fast= fast.next.next;
}
return slow;
}
// LeetCode 206
private ListNode reverseList(ListNode head){
ListNode prev = null;
ListNode cur = head;
while (cur != null) {
ListNode nextNode = cur.next;
cur.next = prev;
prev =cur;
cur = nextNode;
}
return prev;
}
private void mergeList(ListNode head1, ListNode head2) {
ListNode next1 = null;
ListNode next2 = null;
while (head1 != null && head2 != null) {
next1 = head1.next;
next2 = head2.next;
head1.next = head2;
head1 = next1;
head2.next = head1;
head2 = next2;
}
}
82. 删除排序链表中的重复元素 II
难度中等776收藏分享切换为英文接收动态反馈
存在一个按升序排列的链表,给你这个链表的头节点 head ,请你删除链表中所有存在数字重复情况的节点,只保留原始链表中 没有重复出现 的数字。
返回同样按升序排列的结果链表。
示例 1:

输入:head = [1,2,3,3,4,4,5]
输出:[1,2,5]
1).递归实现
public ListNode deleteDuplicates(ListNode head) {
// 没有节点或者只有一个节点,必然没有重复元素
if (head == null || head.next == null) return head;
// 当前节点和下一个节点,值不同,则head的值是需要保留的,对head.next继续递归
if (head.val != head.next.val) {
head.next = deleteDuplicates(head.next);
return head;
} else {
// 当前节点与下一个节点的值重复了,重复的值都不能要。
// 一直往下找,找到不重复的节点。返回对不重复节点的递归结果
ListNode notDup = head.next.next;
while (notDup != null && notDup.val == head.val) {
notDup = notDup.next;
}
return deleteDuplicates(notDup);
}
}
2).利用有序性质一次排序
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode deleteDuplicates(ListNode head) {
// Set<ListNode> set=new HashSet<>();
ListNode dummy=new ListNode(0);
dummy.next=head;
ListNode pre=dummy;
ListNode cur=head;
while(cur!=null&&cur.next!=null){
if(cur.val==cur.next.val){
while(cur!=null&&cur.next!=null &&cur.val==cur.next.val){
cur=cur.next;
}
cur=cur.next;
pre.next=cur;
}else{
pre=pre.next;
cur=cur.next;
}
}
return dummy.next;
}
}
138. 复制带随机指针的链表
难度中等823
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示Node.val的整数。random_index:随机指针指向的节点索引(范围从0到n-1);如果不指向任何节点,则为null。
你的代码 只 接受原链表的头节点 head 作为传入参数。
示例 1:
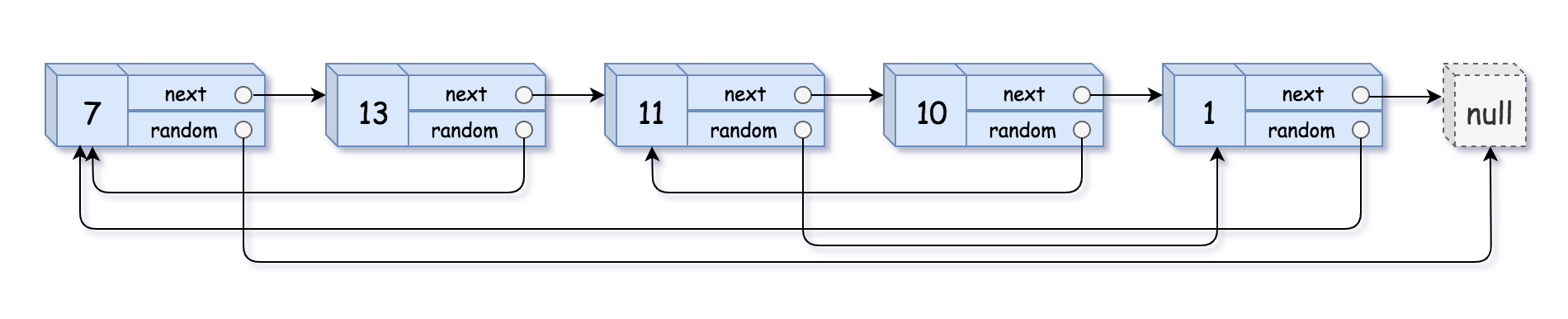
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
迭代
第一步,根据遍历到的原节点创建对应的新节点,每个新创建的节点是在原节点后面,比如下图中原节点1不再指向原原节点2,而是指向新节点1

第二步是最关键的一步,用来设置新链表的随机指针

第三步就简单了,只要将两个链表分离开,再返回新链表就可以了
class Solution {
public Node copyRandomList(Node head) {
if(head==null) {
return null;
}
Node p = head;
//第一步,在每个原节点后面创建一个新节点
//1->1'->2->2'->3->3'
while(p!=null) {
Node newNode = new Node(p.val);
newNode.next = p.next;
p.next = newNode;
p = newNode.next;
}
p = head;
//第二步,设置新节点的随机节点
while(p!=null) {
if(p.random!=null) {
p.next.random = p.random.next;
}
p = p.next.next;
}
Node dummy = new Node(-1);
p = head;
Node cur = dummy;
//第三步,将两个链表分离
while(p!=null) {
cur.next = p.next;
cur = cur.next;
p.next = cur.next;
p = p.next;
}
return dummy.next;
}
}
递归
- 哈希表Mydic映射原有节点->新的节点
- 原节点为空,则返回空
- 原节点在哈希表中可以找到,则说明新的节点已生成,直接返回
- 根据原有节点的值,创建新的节点root = Node(node.val)
- 将原有节点和新节点的对应关系添加到哈希表中Mydic[node] = root
- 最后参照原节点的next和random关系,创建新的next和random节点给新节点root
- 递归整个过程
class Solution {
private HashMap<Node, Node> MyMap = new HashMap<>();
public Node copyRandomList(Node head) {
if (head == null) return null;
if (MyMap.containsKey(head)) return MyMap.get(head);
Node root = new Node(head.val);
MyMap.put(head, root);
root.next = copyRandomList(head.next);
root.random = copyRandomList(head.random);
return root;
}
}
常见题
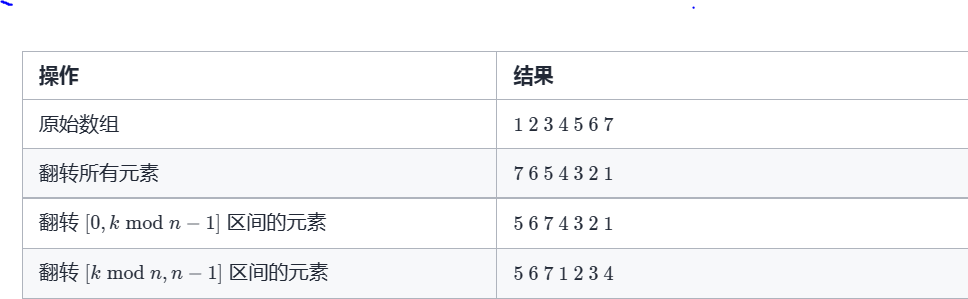
189. 旋转数组
1.方法一:使用额外的数组
class Solution {
public void rotate(int[] nums, int k) {
int n = nums.length;
int[] newArr = new int[n];
for (int i = 0; i < n; ++i) {
newArr[(i + k) % n] = nums[i];
}
System.arraycopy(newArr, 0, nums, 0, n);
}
}
class Solution {
public void rotate(int[] nums, int k) {
if(nums.length<=k) {
k=k%nums.length;
}
k=nums.length-k;
int[] temp=new int[k];
for(int i=0;i<k;i++){
temp[i]=nums[i];
}
for(int i=k;i<nums.length;i++){
nums[i-k]=nums[i];
}
for(int i=0;i<k;i++){
nums[nums.length-k+i]=temp[i];
}
}
}
方法三:数组翻转
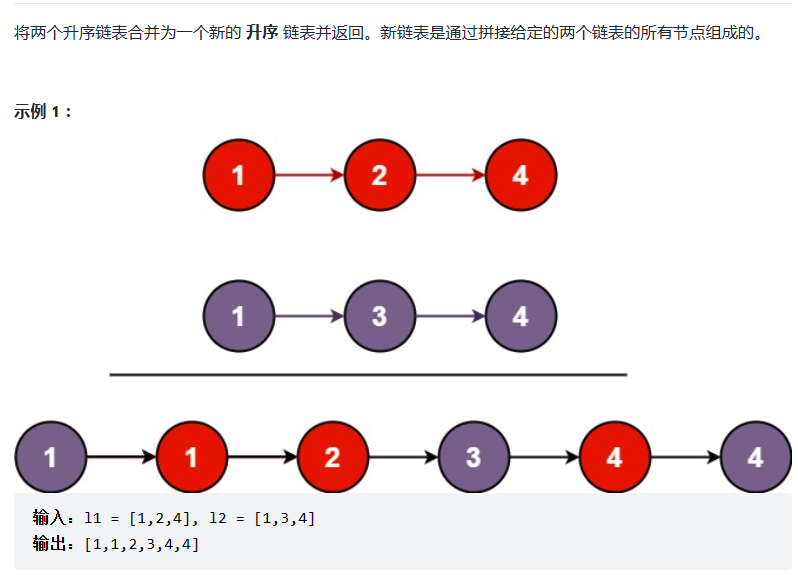
21. 合并两个有序链表
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(0);
ListNode cur=dummy;
while(l1!=null&&l2!=null){
if(l1.val<l2.val){
cur.next=l1;
l1=l1.next;
cur=cur.next;
}else{
cur.next=l2;
l2=l2.next;
cur=cur.next;
}
}
cur.next=l1!=null?l1:l2;
return dummy.next;
}
}
88. 合并两个有序数组
1.合并之后排序
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
for(int i=0;i<n;i++){
nums1[m+i]=nums2[i];
}
Arrays.sort(nums1);
}
}
2.双指针
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int p1 = 0, p2 = 0;
int[] sorted = new int[m + n];
int cur;
while (p1 < m || p2 < n) {
if (p1 == m) {
cur = nums2[p2++];
} else if (p2 == n) {
cur = nums1[p1++];
} else if (nums1[p1] < nums2[p2]) {
cur = nums1[p1++];
} else {
cur = nums2[p2++];
}
sorted[p1 + p2 - 1] = cur;
}
for (int i = 0; i != m + n; ++i) {
nums1[i] = sorted[i];
}
}
}
3.逆序双指针

class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int p1 = m-1, p2 = n-1;
int tail=nums1.length-1;
while(p2>=0){
if(p1<0||nums2[p2]>=nums1[p1]){
nums1[tail--]=nums2[p2--];
}else{
nums1[tail--]=nums1[p1--];
}
}
}
}
66. 加一
class Solution {
public int[] plusOne(int[] digits) {
int n = digits.length;
for (int i = n - 1; i >= 0; --i) {
if (digits[i] != 9) {
++digits[i];
for (int j = i + 1; j < n; ++j) {
digits[j] = 0;
}
return digits;
}
}
// digits 中所有的元素均为 9
int[] ans = new int[n + 1];
ans[0] = 1;
return ans;
}
}



