绍兴集训Day1
Bad Luck Island
题面翻译
给三种人，分别是r,s,p个；
在孤岛上，每两个不同种人相遇则互吃,r吃s,s吃p,p吃r
求最后留下单一种族的概率
题目描述
The Bad Luck Island is inhabited by three kinds of species: $ r $ rocks, $ s $ scissors and $ p $ papers. At some moments of time two random individuals meet (all pairs of individuals can meet equiprobably), and if they belong to different species, then one individual kills the other one: a rock kills scissors, scissors kill paper, and paper kills a rock. Your task is to determine for each species what is the probability that this species will be the only one to inhabit this island after a long enough period of time.
输入格式
The single line contains three integers $ r $ , $ s $ and $ p $ ( $ 1<=r,s,p<=100 $ ) — the original number of individuals in the species of rock, scissors and paper, respectively.
输出格式
Print three space-separated real numbers: the probabilities, at which the rocks, the scissors and the paper will be the only surviving species, respectively. The answer will be considered correct if the relative or absolute error of each number doesn't exceed $ 10^{-9} $ .
样例 #1
样例输入 #1
2 2 2
样例输出 #1
0.333333333333 0.333333333333 0.333333333333
样例 #2
样例输入 #2
2 1 2
样例输出 #2
0.150000000000 0.300000000000 0.550000000000
样例 #3
样例输入 #3
1 1 3
样例输出 #3
0.057142857143 0.657142857143 0.285714285714
解答
采用倒推的方式，设f[r][s][p]为三种生物各有r,s,p时的概率
具体看代码
#include<bits/stdc++.h>
#define rt register int
using namespace std;
int r,s,p;
double f[105][105][105];
double ans1,ans2,ans3;
int main(){
scanf("%d%d%d",&r,&s,&p);
f[r][s][p]=1.0;//可以理解成答案的起点，也可以直接理解成概率为1，毕竟这是给出的明确的初始状态。两种方式殊途同归。
int sum;
for(rt i=r;i>=0;--i)
for(rt j=s;j>=0;--j)
for(rt k=p;k>=0;--k)
{
sum=i*j+j*k+i*k;//r吃s,s吃p·······，一共有这么多种可能性
if(i&&k)f[i-1][j][k]+=1.0*f[i][j][k]*i*k/sum;//当i和k大于0时,p可以吃r
if(j&&i)f[i][j-1][k]+=1.0*f[i][j][k]*i*j/sum;//同理
if(j&&k)f[i][j][k-1]+=1.0*f[i][j][k]*j*k/sum;//这里解释为什么是+=，因为从别的分支语句也能转移到这里，从定义上理解确实是同步的。
if(i&&!j&&!k)ans1+=f[i][j][k];//当j变成0时的可能性累加
if(!i&&j&&!k)ans2+=f[i][j][k];
if(!i&&!j&&k)ans3+=f[i][j][k];
}
printf("%.9lf %.9lf %.9lf",ans1,ans2,ans3);
return 0;
}
[USACO12MAR]Cows in a Skyscraper G
题目描述
A little known fact about Bessie and friends is that they love stair climbing races. A better known fact is that cows really don't like going down stairs. So after the cows finish racing to the top of their favorite skyscraper, they had a problem. Refusing to climb back down using the stairs, the cows are forced to use the elevator in order to get back to the ground floor.
The elevator has a maximum weight capacity of W (1 <= W <= 100,000,000) pounds and cow i weighs C_i (1 <= C_i <= W) pounds. Please help Bessie figure out how to get all the N (1 <= N <= 18) of the cows to the ground floor using the least number of elevator rides. The sum of the weights of the cows on each elevator ride must be no larger than W.
给出n个物品，体积为w[i]，现把其分成若干组，要求每组总体积<=W，问最小分组。(n<=18)
输入格式
* Line 1: N and W separated by a space.
* Lines 2..1+N: Line i+1 contains the integer C_i, giving the weight of one of the cows.
输出格式
* A single integer, R, indicating the minimum number of elevator rides needed.
one of the R trips down the elevator.
样例 #1
样例输入 #1
4 10
5
6
3
7
样例输出 #1
3
提示
There are four cows weighing 5, 6, 3, and 7 pounds. The elevator has a maximum weight capacity of 10 pounds.
We can put the cow weighing 3 on the same elevator as any other cow but the other three cows are too heavy to be combined. For the solution above, elevator ride 1 involves cow #1 and #3, elevator ride 2 involves cow #2, and elevator ride 3 involves cow #4. Several other solutions are possible for this input.
解答
我们在维护时需要两个数据，当前分组数，当前空间剩余数。考虑到DP，得出当前分组的最小数量和当前剩下的最大空间。联系背包问题，这种方式能通过记忆化搜索实现。
有了状态，考虑如何转移。
分类讨论：
- 当前最大空间能再放下一个
- 当前空间无法再放下一个
注意初始状态的设置。
#include<bits/stdc++.h>
#define rt register int
using namespace std;
int n,W,w[20],dpv[270000],dpcnt[270000];
int main(){
scanf("%d%d",&n,&W);
for(rt i=1;i<=n;++i)
scanf("%d",&w[i]);
int chose=(1<<n)-1;
memset(dpcnt,0x3f,sizeof(dpcnt));
dpcnt[0]=1;
memset(dpv,0,sizeof dpv);
dpv[0]=W ;
for(rt i=0;i<=chose;++i)
for(rt j=1;j<=n;++j){
if(i&(1<<(j-1)))continue;
if(dpv[i]>=w[j]){
dpcnt[i|(1<<(j-1))]=min(dpcnt[i|(1<<(j-1))],dpcnt[i]);
dpv[i|(1<<(j-1))]=max(dpv[i|(1<<(j-1))],dpv[i]-w[j]);
// printf("1:dpcnt[%d|(1<<(%d-1))]=%d\n",i,j,dpcnt[i|(1<<(j-1))]);
// printf("1:dpv[%d|(1<<(%d-1))]=%d\n",i,j,dpv[i|(1<<(j-1))]);
}else{
dpcnt[i|(1<<(j-1))]=min(dpcnt[i|(1<<(j-1))],dpcnt[i]+1);
dpv[i|(1<<(j-1))]=max(dpv[i|(1<<(j-1))],W -w[j]);
// printf("2:dpcnt[%d|(1<<(%d-1))]=%d\n",i,j,dpcnt[i|(1<<(j-1))]);
// printf("2:dpv[%d|(1<<(%d-1))]=%d\n",i,j,dpv[i|(1<<(j-1))]);
}
}
// for(rt i=1;i<=chose;++i)
printf("%d",dpcnt[chose]);
return 0;
}
Choosing Capital for Treeland
题面翻译
题目描述
Treeland国有n个城市，这n个城市连成了一颗树，有n-1条道路连接了所有城市。每条道路只能单向通行。现在政府需要决定选择哪个城市为首都。假如城市i成为了首都，那么为了使首都能到达任意一个城市，不得不将一些道路翻转方向，记翻转道路的条数为k。你的任务是找到所有满足k最小的首都。
输入输出格式
输入格式
输入包含多个测试点。对于每个测试点，每个测试点的第一行为一个正整数n（2<=n<=2e5）。接下来n-1行，每行两个正整数ai，bi，表示城市a到城市b有一条单向通行的道路。输入以空格分隔，以EOF结尾。
输出格式
对于每个测试点，第一行输出k，第二行升序输出所有满足条件的首都的编号。
题目描述
The country Treeland consists of $ n $ cities, some pairs of them are connected with unidirectional roads. Overall there are $ n-1 $ roads in the country. We know that if we don't take the direction of the roads into consideration, we can get from any city to any other one.
The council of the elders has recently decided to choose the capital of Treeland. Of course it should be a city of this country. The council is supposed to meet in the capital and regularly move from the capital to other cities (at this stage nobody is thinking about getting back to the capital from these cities). For that reason if city $ a $ is chosen a capital, then all roads must be oriented so that if we move along them, we can get from city $ a $ to any other city. For that some roads may have to be inversed.
Help the elders to choose the capital so that they have to inverse the minimum number of roads in the country.
输入格式
The first input line contains integer $ n $ ( $ 2<=n<=2·10^{5} $ ) — the number of cities in Treeland. Next $ n-1 $ lines contain the descriptions of the roads, one road per line. A road is described by a pair of integers $ s_{i},t_{i} $ ( $ 1<=s_{i},t_{i}<=n; s_{i}≠t_{i} $ ) — the numbers of cities, connected by that road. The $ i $ -th road is oriented from city $ s_{i} $ to city $ t_{i} $ . You can consider cities in Treeland indexed from 1 to $ n $ .
输出格式
In the first line print the minimum number of roads to be inversed if the capital is chosen optimally. In the second line print all possible ways to choose the capital — a sequence of indexes of cities in the increasing order.
样例 #1
样例输入 #1
3
2 1
2 3
样例输出 #1
0
2
样例 #2
样例输入 #2
4
1 4
2 4
3 4
样例输出 #2
2
1 2 3
解答
这道题犇犇说是裸的换根DP。
1.第一次深搜初始化
2.第二次深搜转移
设dp[i]为以i点作为首都时需要翻转的道路数。
这里有个对应技巧:
- 虽然是单向边，但我们可以按照无向图来存图，这里0表示顺，1表示逆，这样处理有利于后期计算
- 神奇的深搜
- 换根时，如果首都从u到v转移，而存在一条从u到v的边。那么相当于dp[v]=dp[u]-1(思考为什么-1，打字比较麻烦）,如果存在的是一条从v到u的边，dp[v]=dp[u]+1。
#include<bits/stdc++.h>
#define rt register int
using namespace std;
struct edge{
int to,nxt,w;
}edges[500005];
int idx,h[200005],n,dp[200005],ans=0x3f3f3f3f;
inline void add(int u,int v,int w){
edges[++idx].to=v;edges[idx].w=w;edges[idx].nxt=h[u];h[u]=idx;
}
inline void dfs1(int u,int fa){
for(rt i=h[u];i;i=edges[i].nxt){
int v=edges[i].to;
if(v==fa)continue;
dfs1(v,u);
dp[u]+=dp[v]+edges[i].w;
}
}
inline void dfs2(int u,int fa){
for(rt i=h[u];i;i=edges[i].nxt){
int v=edges[i].to;
if(v==fa)continue;
dp[v]=dp[u]+(edges[i].w?-1:1);
dfs2(v,u);
}
}
int main(){
while(~scanf("%d",&n))
{
idx=0;
memset(h,0,sizeof h);
int u,v;
for(rt i=1;i<n;++i)
{
scanf("%d%d",&u,&v);
add(u,v,0);add(v,u,1);
}
memset(dp,0,sizeof dp);
dfs1(1,-1);
dfs2(1,-1);
ans=0x3f3f3f3f;
for(rt i=1;i<=n;++i)
ans=min(ans,dp[i]);
printf("%d\n",ans);
for(rt i=1;i<=n;++i)
if(dp[i]==ans)printf("%d ",i);
puts("");
}
return 0;
}
[CSP-S2019] Emiya 家今天的饭
题目描述
Emiya 是个擅长做菜的高中生，他共掌握 \(n\) 种烹饪方法，且会使用 \(m\) 种主要食材做菜。为了方便叙述，我们对烹饪方法从 \(1 \sim n\) 编号，对主要食材从 \(1 \sim m\) 编号。
Emiya 做的每道菜都将使用恰好一种烹饪方法与恰好一种主要食材。更具体地，Emiya 会做 \(a_{i,j}\) 道不同的使用烹饪方法 \(i\) 和主要食材 \(j\) 的菜（\(1 \leq i \leq n, 1 \leq j \leq m\)），这也意味着 Emiya 总共会做 \(\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m} a_{i,j}\) 道不同的菜。
Emiya 今天要准备一桌饭招待 Yazid 和 Rin 这对好朋友，然而三个人对菜的搭配有不同的要求，更具体地，对于一种包含 \(k\) 道菜的搭配方案而言：
- Emiya 不会让大家饿肚子，所以将做至少一道菜，即 \(k \geq 1\)
- Rin 希望品尝不同烹饪方法做出的菜，因此她要求每道菜的烹饪方法互不相同
- Yazid 不希望品尝太多同一食材做出的菜，因此他要求每种主要食材至多在一半的菜（即 \(\lfloor \frac{k}{2} \rfloor\) 道菜）中被使用
这里的 \(\lfloor x \rfloor\) 为下取整函数，表示不超过 \(x\) 的最大整数。
这些要求难不倒 Emiya，但他想知道共有多少种不同的符合要求的搭配方案。两种方案不同，当且仅当存在至少一道菜在一种方案中出现，而不在另一种方案中出现。
Emiya 找到了你，请你帮他计算，你只需要告诉他符合所有要求的搭配方案数对质数 \(998,244,353\) 取模的结果。
输入格式
第 1 行两个用单个空格隔开的整数 \(n,m\)。
第 2 行至第 \(n + 1\) 行，每行 \(m\) 个用单个空格隔开的整数，其中第 \(i + 1\) 行的 \(m\) 个数依次为 \(a_{i,1}, a_{i,2}, \cdots, a_{i,m}\)。
输出格式
仅一行一个整数，表示所求方案数对 \(998,244,353\) 取模的结果。
样例 #1
样例输入 #1
2 3
1 0 1
0 1 1
样例输出 #1
3
样例 #2
样例输入 #2
3 3
1 2 3
4 5 0
6 0 0
样例输出 #2
190
样例 #3
样例输入 #3
5 5
1 0 0 1 1
0 1 0 1 0
1 1 1 1 0
1 0 1 0 1
0 1 1 0 1
样例输出 #3
742
提示
【样例 1 解释】
由于在这个样例中，对于每组 \(i, j\)，Emiya 都最多只会做一道菜，因此我们直接通过给出烹饪方法、主要食材的编号来描述一道菜。
符合要求的方案包括：
- 做一道用烹饪方法 1、主要食材 1 的菜和一道用烹饪方法 2、主要食材 2 的菜
- 做一道用烹饪方法 1、主要食材 1 的菜和一道用烹饪方法 2、主要食材 3 的菜
- 做一道用烹饪方法 1、主要食材 3 的菜和一道用烹饪方法 2、主要食材 2 的菜
因此输出结果为 \(3 \bmod 998,244,353 = 3\)。 需要注意的是，所有只包含一道菜的方案都是不符合要求的，因为唯一的主要食材在超过一半的菜中出现，这不满足 Yazid 的要求。
【样例 2 解释】
Emiya 必须至少做 2 道菜。
做 2 道菜的符合要求的方案数为 100。
做 3 道菜的符合要求的方案数为 90。
因此符合要求的方案数为 100 + 90 = 190。
【数据范围】
| 测试点编号 | \(n=\) | \(m=\) | \(a_{i,j}<\) | 测试点编号 | \(n=\) | \(m=\) | \(a_{i,j}<\) |
|---|---|---|---|---|---|---|---|
| \(1\) | \(2\) | \(2\) | \(2\) | \(7\) | \(10\) | \(2\) | \(10^3\) |
| \(2\) | \(2\) | \(3\) | \(2\) | \(8\) | \(10\) | \(3\) | \(10^3\) |
| \(3\) | \(5\) | \(2\) | \(2\) | \(9\sim 12\) | \(40\) | \(2\) | \(10^3\) |
| \(4\) | \(5\) | \(3\) | \(2\) | \(13\sim 16\) | \(40\) | \(3\) | \(10^3\) |
| \(5\) | \(10\) | \(2\) | \(2\) | \(17\sim 21\) | \(40\) | \(500\) | \(10^3\) |
| \(6\) | \(10\) | \(3\) | \(2\) | \(22\sim 25\) | \(100\) | \(2\times 10^3\) | \(998244353\) |
对于所有测试点，保证 \(1 \leq n \leq 100\)，\(1 \leq m \leq 2000\)，\(0 \leq a_{i,j} \lt 998,244,353\)。
解答
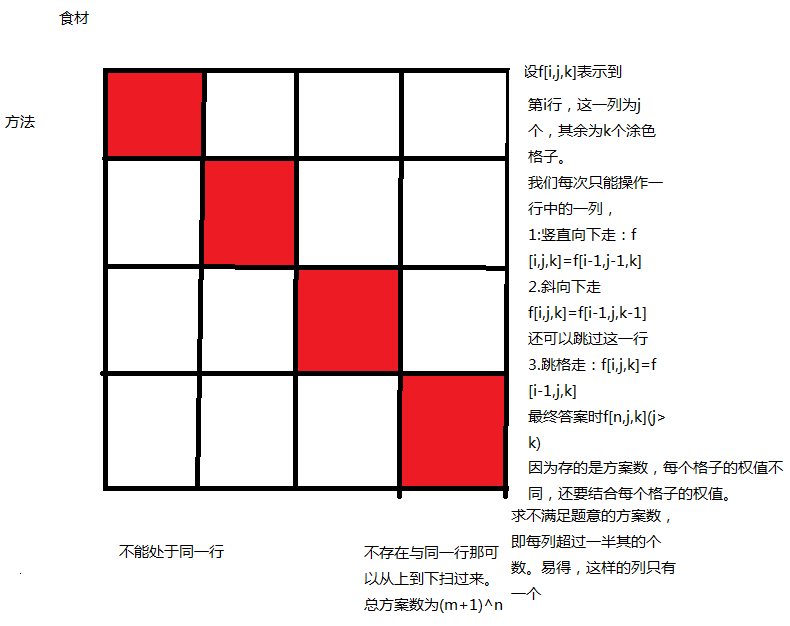
这道题可以看成一个anm的矩阵，每行只能选一个，每列不能选超过一半个。因为所有方案很好求，也就是每列的总和+1相乘-1（一个都不选），只需要算不合法的方案数。有一个性质是不合法的列只能有一个。那么枚举每一列，用dp维护
设dp[i,j,k]表示到第i行，这一列选了j个，其它列选了k个
dp[i,j,k]=dpi-1,j,k+dp[i-1,j-1,k]a[i][col]（col表示当前这一列）(表示选这一列）+dp[i-1,j,k-1](sum[i]-a[i][col])(sum是一行的和，表示选其它列）
如果是这样，时间复杂度是过不去的。但分也挺高
因为真正有用的是j>k的情况。可以用j-k来做一个下标。但这样的下标最小为-n。我们给它一个偏移量全部+n
#include<bits/stdc++.h>
#define mod 998244353
#define ll long long
using namespace std;
const int MAXN = 105, MAXM = 2005;
int n,m,a[MAXN][MAXM],sum[MAXN];
ll f[MAXN][MAXN*2];
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
sum[i]=(sum[i]+a[i][j])%mod;
}
ll ans=0;
for(int col=1;col<=m;col++)
{
memset(f,0,sizeof(f));
f[0][n]=1;
for(int i=1;i<=n;i++)
for(int j=n-i;j<=n+i;j++)
f[i][j]=(f[i-1][j]+f[i-1][j-1]*a[i][col]%mod+f[i-1][j+1]*(sum[i]-a[i][col])%mod)%mod;
for(int j=1;j<=n;j++)
ans=(ans+f[n][n+j])%mod;
}
// printf("ans:%lld\n",ans);
long long summ=1;
for(int i=1;i<=n;++i)
summ=(summ*(sum[i]+1))%mod;
--summ;
printf("%lld",(-ans+mod+summ)%mod);
return 0;
}
