数字组合（算法竞赛进阶指南）

278. 数字组合 - AcWing题库

给定 N 个正整数 A1,A2,…,AN，从中选出若干个数，使它们的和为 M，求有多少种选择方案。

输入格式

第一行包含两个整数 N 和 M。

第二行包含 N 个整数，表示 A1,A2,…,AN。

输出格式

包含一个整数，表示可选方案数。

数据范围

1≤N≤100,

1≤M≤10000,

1≤Ai≤1000,

答案保证在 int 范围内。

输入样例：

4 4

1 1 2 2

输出样例：

3

1.把题意理解成在一个体积为M的背包里，放入体积为Ai的物品；

2.状态确立：f[i][j]表示装入第i个物品已用j体积时总方案的数量

3.状态转移：

1.加入第i个物品：f[i][j] += f[i - 1][j - v[i]]

2.不加入 ： f[i][j] += f[i - 1][j]

 4.滚动数组优化：

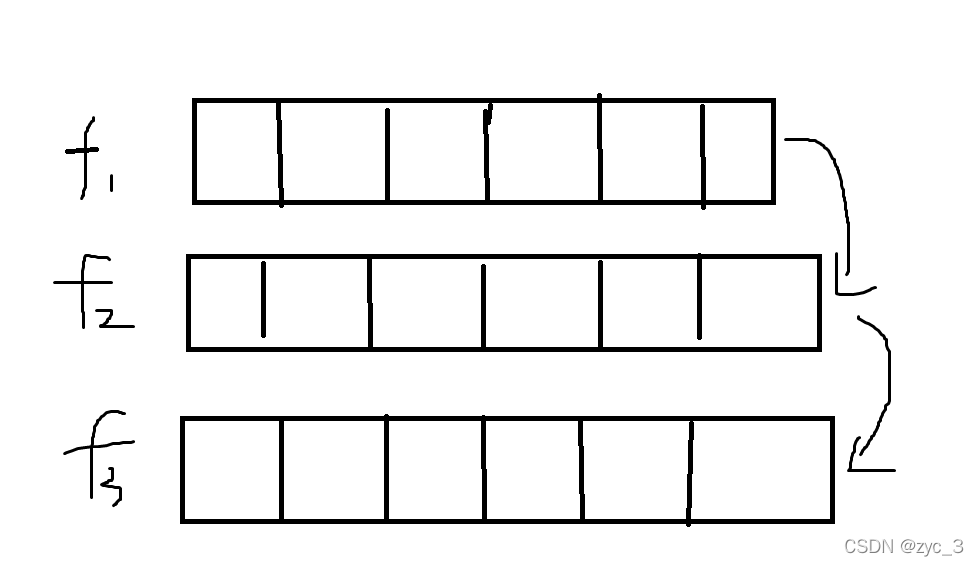
 我们每一次更新f数组，都是从i - 1状态时的数组转移过来的。

每一次更新时所用的数据都是上一次的数组，就像一次一次滚动一样。

只需要同时存在一个数组就可以完成所有过程,所以把i的那一维消掉，变成f[j]。

但这么做有一个条件。

比如我们在更新f[j] += f[j - v[i]]时，f[j - v[i]]尚且用的是上一次留下（未更新的f数组）。但假设我们的j是从小到大遍历的，我们之后的f[j] += f[j - v[i]]中的f[j - v[i]]，可能是由这次循环中被更新的数据而并非上次循环的数据。也就是说v[i]被无限使用了（这也是为什么完全背包j是从小到大遍历的）。

为了避免这种错误，我们需要让j从大到小遍历，这种做法往往和滚动数组搭配使用。

滚动数组是我们降维从而减小空间复杂度（往往是数组大小）的重要手段。

滚动数组不会减小时间复杂度。

5.代码

消去i后不放的情况变为f[i + 1][j] += f[i][j],循环会自动实现所以不用管

#include<bits/stdc++.h>

using namespace std;

const int N = 10010;

int n,m;
int f[N];

int main()
{
    cin >> n >> m;
    f[0] = 1;
    for(int i = 0;i < n;i ++)
    {
        int v;
        cin >> v;
        for(int j = m;j >= v;j --)f[j] += f[j - v];
    }

    cout << f[m] << endl;

    return 0;
}