多边形（算法竞赛进阶指南）
“多边形游戏”是一款单人益智游戏。
游戏开始时，给定玩家一个具有 N 个顶点 N 条边（编号 1∼N）的多边形，如图 1 所示，其中 N=4。
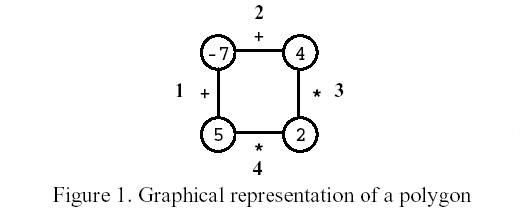
每个顶点上写有一个整数，每个边上标有一个运算符 +（加号）或运算符 *（乘号）。
第一步，玩家选择一条边，将它删除。
接下来在进行 N−1 步，在每一步中，玩家选择一条边，把这条边以及该边连接的两个顶点用一个新的顶点代替，新顶点上的整数值等于删去的两个顶点上的数按照删去的边上标有的符号进行计算得到的结果。
下面是用图 1 给出的四边形进行游戏的全过程。
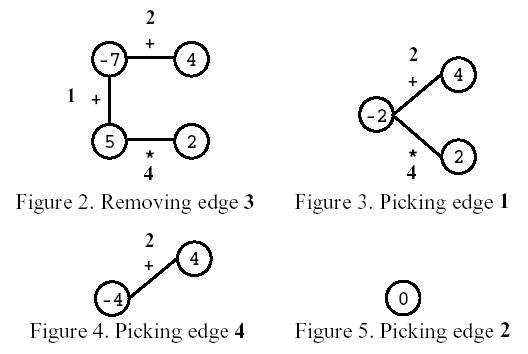
最终，游戏仅剩一个顶点，顶点上的数值就是玩家的得分，上图玩家得分为 0。
请计算对于给定的 N 边形，玩家最高能获得多少分，以及第一步有哪些策略可以使玩家获得最高得分。
输入格式
输入包含两行，第一行为整数 N。
第二行用来描述多边形所有边上的符号以及所有顶点上的整数，从编号为 1 的边开始，边、点、边…按顺序描述。
其中描述顶点即为输入顶点上的整数，描述边即为输入边上的符号，其中加号用 t 表示，乘号用 x 表示。
输出格式
输出包含两行，第一行输出最高分数。
在第二行，将满足得到最高分数的情况下，所有的可以在第一步删除的边的编号从小到大输出，数据之间用空格隔开。
数据范围
3≤N≤50,
数据保证无论玩家如何操作，顶点上的数值均在 [−32768,32767] 之内。
输入样例：
4
t -7 t 4 x 2 x 5
输出样例：
33
1 2
区间DP引入：石子合并（算法竞赛进阶指南）_zyc_3的博客-CSDN博客
在本题中，我们的对象是一个环。在区间DP中，有破环成链的方法。
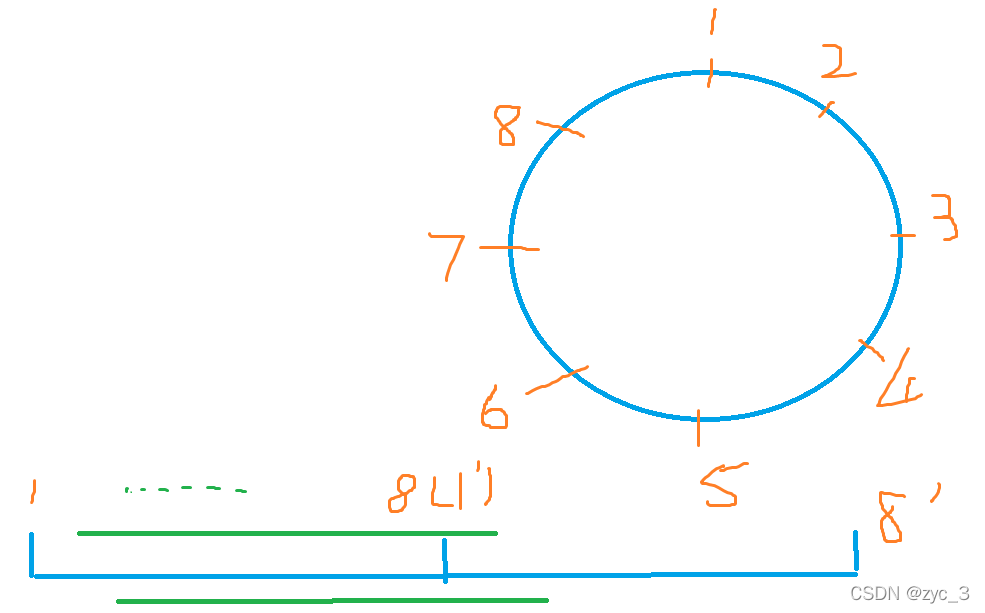
如图，我们把一个环拆成两个相同的首尾向连的链。对于这个环的每一顶点，我们都有对应的一条破环成链之法。我们每次从这个长度为2n的环里取出一条长度为n的链，如f[2][9],相当于把环从2点拆开，变成2 3 4 5 6 7 8 1。至此，我们把环转化为链。
状态确立：
f[l][r]为将环从l,r合为一个点的最大值。
状态转移：
1.f[l][r] = f[l][k] + f[k + 1][r]
2.f[l][r] = f[l][k] * f[]k + 1][r]
第一种是成立的，第二种是不成立的
10*10< -50 * -50
所以我们不仅要存最大值，还要存最小值。
状态确立
f[l][r]为将环从l,r合为一个点的最大值。
g[l][r]为将环从l,r合为一个点的最小值。
状态转移
1.加：f[l][r] = f[l][k] + f[k + 1][r]
：g[l][r] = g[l][k] + g[k + 1][r]
2.乘：
虽然一共有九种可能，但实际有用的就四种。
在求最大的过程中，我们需要算
1.最大的*最大的
2.最小的*最小的
3.最小的*最大的
4.最大的*最小的
（左边是f1,g1，右边是f2,g2）
我们不在乎谁是正谁是负，全部算出来。实际就四种方式
x1 = maxl * maxr, x2 = maxl * minr, x3 = minl * maxr, x4 = minl * minr;
f[l][r] = max(f[l][r], max(max(x1, x2), max(x3, x4)));
g[l][r] = min(g[l][r], min(min(x1, x2), min(x3, x4)));
代码：
#include<bits/stdc++.h>
using namespace std;
const int N = 110, INF = 32768;
int n;
int w[N];
char c[N];
int f[N][N], g[N][N];
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ )
{
cin >> c[i] >> w[i];
c[i + n] = c[i];
w[i + n] = w[i];
}//破环成链
for (int len = 1; len <= n; len ++ )//先枚举区间
for (int l = 1; l + len - 1 <= n * 2; l ++ )
{
int r = l + len - 1;
if (len == 1) f[l][r] = g[l][r] = w[l];//初始化
else
{
f[l][r] = -INF, g[l][r] = INF;//初始化时最大值设为最小值，最小值设为最大值
for (int k = l; k < r; k ++ )
{
char op = c[k + 1];
int minl = g[l][k], minr = g[k + 1][r];
int maxl = f[l][k], maxr = f[k + 1][r];
if (op == 't')
{
f[l][r] = max(f[l][r], maxl + maxr);
g[l][r] = min(g[l][r], minl + minr);
}
else
{
int x1 = maxl * maxr, x2 = maxl * minr, x3 = minl * maxr, x4 = minl * minr;
f[l][r] = max(f[l][r], max(max(x1, x2), max(x3, x4)));
g[l][r] = min(g[l][r], min(min(x1, x2), min(x3, x4)));
}
}
}
}
int res = -INF;
for (int i = 1; i <= n; i ++ ) res = max(res, f[i][i + n - 1]);
cout << res << endl;
//倒推求具体状态
for (int i = 1; i <= n; i ++ )
if (res == f[i][i + n - 1])
cout << i << ' ';
return 0;
}
