金字塔（算法竞赛进阶指南）
虽然探索金字塔是极其老套的剧情，但是有一队探险家还是到了某金字塔脚下。
经过多年的研究，科学家对这座金字塔的内部结构已经有所了解。
首先，金字塔由若干房间组成，房间之间连有通道。
如果把房间看作节点，通道看作边的话，整个金字塔呈现一个有根树结构，节点的子树之间有序，金字塔有唯一的一个入口通向树根。
并且，每个房间的墙壁都涂有若干种颜色的一种。
探险队员打算进一步了解金字塔的结构，为此，他们使用了一种特殊设计的机器人。
这种机器人会从入口进入金字塔，之后对金字塔进行深度优先遍历。
机器人每进入一个房间（无论是第一次进入还是返回），都会记录这个房间的颜色。
最后，机器人会从入口退出金字塔。
显然，机器人会访问每个房间至少一次，并且穿越每条通道恰好两次（两个方向各一次）， 然后，机器人会得到一个颜色序列。
但是，探险队员发现这个颜色序列并不能唯一确定金字塔的结构。
现在他们想请你帮助他们计算，对于一个给定的颜色序列，有多少种可能的结构会得到这个序列。
因为结果可能会非常大，你只需要输出答案对109 取模之后的值。
输入格式
输入仅一行，包含一个字符串 S，长度不超过 300，表示机器人得到的颜色序列。
输出格式
输出一个整数表示答案。
输入样例：
ABABABA
输出样例：
5
前置内容：
DFS序列：
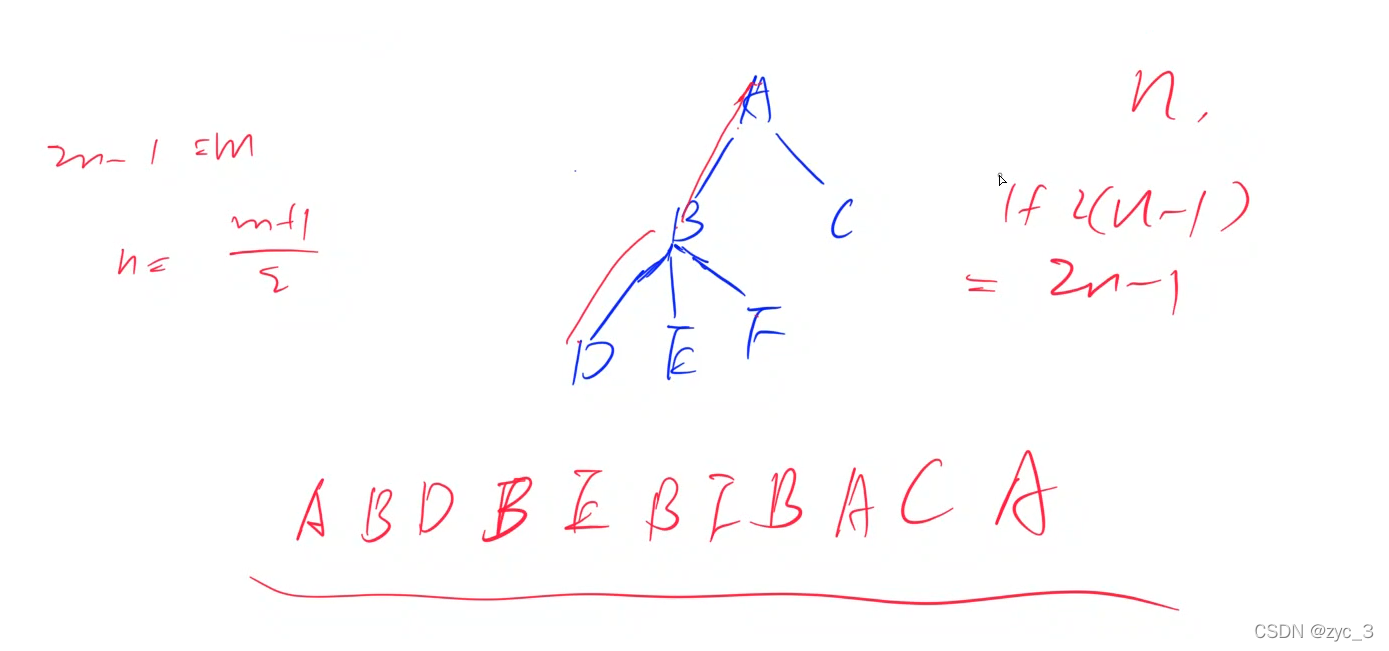
如图，从点A出发到B，从点B出发到D，从点D出发返回B，从点B出发到E，从点E出发返回B······从点A出发到C，从点C出发到A。
从而得到DFS序列：ABDBEBFBACA
像不像一笔画。
知道流程后，我们可以发现一个规律，对于每一条边，我们都往返一次，共经历两次，对于n个顶点，我们有n - 1条边，而每一次经过边，都会搜索到一个点，所以DFS序列的长度为1（出发点） + 2 * （n - 1）= 2 * n - 1。
输入样例：
ABABABA
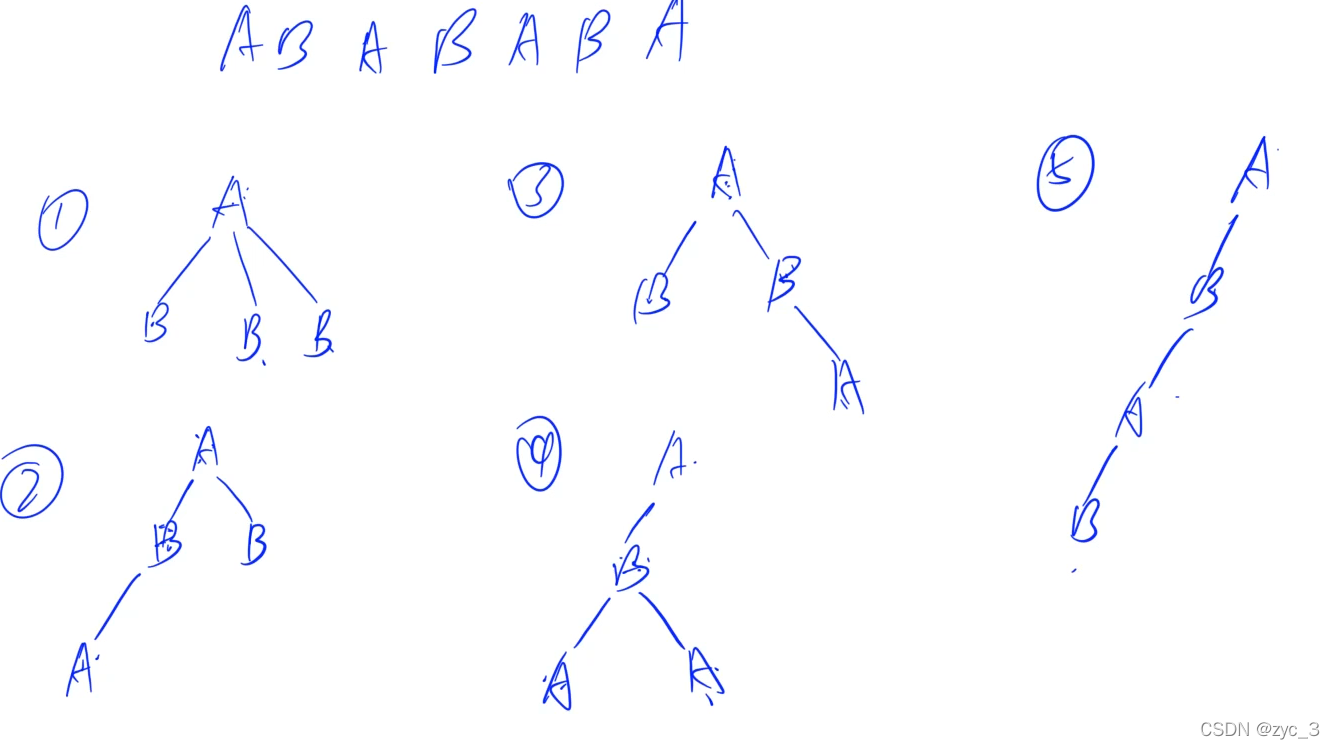
在样例中，DFS序列的长度为7，代入可得顶点的个数为4。
样例解释：
状态确立：
(这里R - 1是不合法的，因为最后一个点是n，R - 1不是一个DFS序列，最多是R - 2）
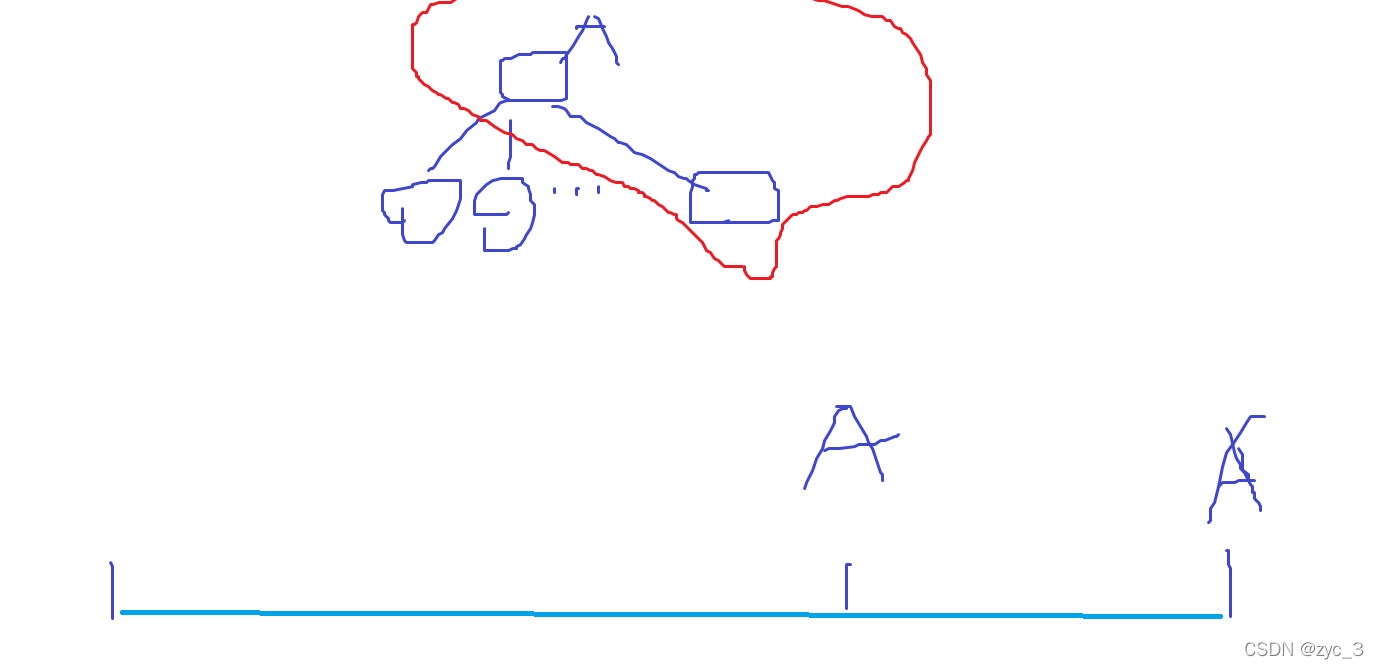
我们把一整条DFS序列拆出一个子链，那么这个子链是由红圈中的部分贡献的DFS序列。
但这些状态不是全部都成立的，合理的状态需要满足一个条件
K,L,R代表的字母必须相同
状态转移：
我们把树分为两部分，总的方案数为两方的方案数之积。
所以是f[L,R] = f[L,K] * f[K + 1,R]吗？
我们的方案数是左边的子树 * 右边的子树。
左边的子树是[L,R],右边的子树是[K + 1,R - 1]。
所以状态转移：
f[L,R] = f[L,K] * f[K + 1,R - 1]
我们最后再把所有不同种树的方案数相加，就得到最后的答案。
关于区间DP枚举方式的一点介绍：石子合并（算法竞赛进阶指南）_zyc_3的博客-CSDN博客
代码：
#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9;
typedef long long ll;
ll f[305][305];
string st;
int n;
int main()
{
cin >> st;
n = st.size();
if(n % 2 == 0){
cout << 0;
}//判断是否有解
else{
for(int len = 1;len <= n;len += 2)//len的变化是因为每次子树的点数变化，一个点对应来回两次，对DFS序列贡献为2
{
for(int l = 0;l + len - 1 < n;l ++)
{
int r = l + len - 1;
if(len == 1)f[l][r] = 1;//初始化
else if(st[l] == st[r]){
for(int k = l;k < r;k += 2)//k += 2的理由同上
{
if(st[k] == st[l])f[l][r] = (f[l][r] + f[l][k] * f[k + 1][r - 1]) % mod;//取不同的k值产生的f[l][r]要求总和
}
}
}
}
cout << f[0][n - 1];
}
return 0;
}
