数论（未完待续）
这里只贴板子，就不证明了，说实话，NOIP完全不需要你去掌握各种复杂的证明。只要会优化就行。
P3383 【模板】线性筛素数
#include <cstdio>
#include <cstring>
bool isPrime[100000010];
//isPrime[i] == 1表示：i是素数
int Prime[6000010], cnt = 0;
//Prime存质数
void GetPrime(int n)//筛到n
{
memset(isPrime, 1, sizeof(isPrime));
//以“每个数都是素数”为初始状态，逐个删去
isPrime[1] = 0;//1不是素数
for(int i = 2; i <= n; i++)
{
if(isPrime[i])//没筛掉
Prime[++cnt] = i; //i成为下一个素数
for(int j = 1; j <= cnt && i*Prime[j] <= n/*不超上限*/; j++)
{
//从Prime[1]，即最小质数2开始，逐个枚举已知的质数，并期望Prime[j]是(i*Prime[j])的最小质因数
//当然，i肯定比Prime[j]大，因为Prime[j]是在i之前得出的
isPrime[i*Prime[j]] = 0;
if(i % Prime[j] == 0)//保证prime[j]是i的最小质因数
break; //“最小质因数 × 最大因数（非自己） = 这个合数”
}
}
}
int main()
{
int n, q;
scanf("%d %d", &n, &q);
GetPrime(n);
while (q--)
{
int k;
scanf("%d", &k);
printf("%d\n", Prime[k]);
}
return 0;
}快速幂
#include<bits/stdc++.h>
using namespace std;
long long b,a,p,k,ans=1,c;
int main()
{
scanf("%d%d%d",&b,&p,&k);
a=b;c=p;
while(p>0)
{
if(p%2!=0)
ans=ans*b%k;
b=b*b%k;
p=p>>1;
}
ans %= k;
printf("%d^%d mod %d=%d",a,c,k,ans);
return 0;
}裴蜀定理
裴蜀定理得名于法国数学家艾蒂安·裴蜀，说明了对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性丢番图方程（称为裴蜀等式）： ax + by = m 有解当且仅当m是d的倍数。
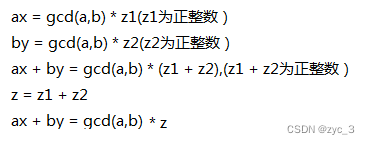
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
inline int gcd(int x, int y) {
return y ? gcd(y, x%y) : x;
}
int n;
int main() {
scanf("%d", &n);
int ans = 0, tmp;
for(int i=1; i<=n; i++) {
scanf("%d", &tmp);
if(tmp < 0) tmp = -tmp;
ans = gcd(ans, tmp);
}
printf("%d", ans);
}求逆元：
逆元的意义就是在%的运算中把除法转换为乘法
扩展欧几里得：
#include<bits/stdc++.h>
using namespace std;
int exgcd(int a, int b, int &x, int &y){//返回gcd(a,b) 并求出解(引用带回),每次函数中值的改动要传回上一层函数
if(b==0){
x = 1, y = 0;
return a;
}
int x1,y1,gcd;
gcd = exgcd(b, a%b, x1, y1);
x = y1, y = x1 - a/b*y1;
return gcd;
}
int main(){
int n,a,b,x,y;
cin>>n;
while(n--){
cin>>a>>b;
exgcd(a,b,x,y);
cout<<x<<" "<<y<<endl;
}
return 0;
}
/*
因为
gcd(a,b)=gcd(b,a%b)
而
bx′+(a%b)y′=gcd(b,a%b)
等于
bx′+(a−⌊a/b⌋∗b)y′=gcd(b,a%b)
转化
ay′+b(x′−⌊a/b⌋∗y′)=gcd(b,a%b)=gcd(a,b)
故而
x=y′,y=x′−⌊a/b⌋∗y′
*/ax+by=c
x′=x0∗c/d,y′=y0∗c/d
应用: 求解一次同余方程 ax≡b(modm)则等价于求
ax=m∗(−y)+b//从%的定义出发
ax+my=b
有解条件为gcd(a,m)|b,然后用扩展欧几里得求解即可
特殊情况 当 b=1且 a与m互质时 则所求的x即为a的逆元
void Exgcd(ll a, ll b, ll &x, ll &y) {
if (!b) x = 1, y = 0;
else Exgcd(b, a % b, y, x), y -= a / b * x;
}
int main() {
ll x, y;
Exgcd (a, p, x, y);
x = (x % p + p) % p;
printf ("%d\n", x); //x是a在mod p下的逆元
}快速幂：配合费马小定理
若p为素数，a为正整数，且a、p互质。
则有a^（p−1）≡1(mod p)
a∗x≡1(mod p)
a∗x≡a^(p−1)(mod p)
x≡a^(p−2)(mod p)
所以我们可以用快速幂来算出 ap−2(modp)ap−2(modp)的值，这个数就是它的逆元了
线性算法：
前置：
首先我们有一个,1^−1≡1(mod p)
然后设 p=k∗i+r,(1<r<i<p) 也就是 k 是 p/i的商，r 是余数 。
再将这个式子放到(mod p)意义下就会得到：
k∗i+r≡0(mod p)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3000010;
int inv[N],n,p;
int main()
{
scanf("%d%d",&n,&p);
inv[1] = 1;
puts("1");
for(int i = 2;i <= n;i ++)
{
inv[i] = (ll)(p - p / i) * inv[p % i] % p;
printf("%d\n",inv[i]);
}
return 0;
}PS：(-p/i+p)防止负数
线性求组合数
这里直接贴卢卡斯定理的例题，题目在洛谷P3807
#include<bits/stdc++.h>
#define mod 1000000007
using namespace std;
typedef long long LL;
const int maxn=2e5+7;
LL a[maxn],b[maxn];
LL Lucas(LL n,LL m,LL p)
{
if(n<m) return 0;
else if(n<p) return (b[n]*a[m]%p)*a[n-m]%p;
else return Lucas(n/p,m/p,p)*Lucas(n%p,m%p,p)%p;
}
int main()
{
LL n,m,p,t;
scanf("%lld",&t);
while(t--)
{
scanf("%lld%lld%lld",&n,&m,&p);
a[0]=a[1]=b[0]=b[1]=1;
for(int i=2;i<=n+m;i++) b[i]=b[i-1]*i%p;
for(int i=2;i<=n+m;i++) a[i]=(p-p/i)*a[p%i]%p;
for(int i=2;i<=n+m;i++) a[i]=a[i-1]*a[i]%p;
printf("%lld\n",Lucas(n+m,m,p));
}
}
欧拉函数
例题见洛谷P5091
#include <cstdio>
#include <ctype.h>
#include <cstring>
#include <algorithm>
#define ll long long
int a, b, m, phi, ans = 1;
bool flag;
inline int read() {
int f = 1, w = 0; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) {
w = (w << 3) + (w << 1) + (ch ^ '0');
if (w >= phi) {
flag = true;
w %= phi;
}
}
return f * w;
}
void GetPhi() {
int tmp = m;
phi = m;
for (int i = 2; i * i <= m; ++ i) {
if (! (tmp % i)) {
phi = phi - phi / i;
while (! (tmp % i)) tmp /= i;
}
}
if (tmp > 1) phi = phi - phi / tmp;
}
int QuickPow(int x, int y) {
int ret = 1;
while (y) {
if (y & 1) ret = 1ll * ret * x % m;
x = 1ll * x * x % m, y >>= 1;
}
return ret;
}
int main() {
scanf("%d%d", &a, &m);
GetPhi();
b = read();
if (flag) b += phi;
printf("%d", QuickPow(a, b));
return 0;
}
扩展中国剩余定理
例题洛谷P4777 题解区第一篇有很好的解释
#include<bits/stdc++.h>
using namespace std;
#define LL long long
int n;
LL m[100005],c[100005];
LL gcd(LL a,LL b)
{
return !b?a:gcd(b,a%b);
}
LL exgcd(LL a, LL b, LL &x, LL &y){
if(b==0){
x = 1, y = 0;
return a;
}
LL x1,y1,gcd;
gcd = exgcd(b, a%b, x1, y1);
x = y1, y = x1 - a/b*y1;
return gcd;
}
LL getInv(LL a,LL mod)
{
LL x,y;
LL d=exgcd(a,mod,x,y);
return d==1?(x+mod)%mod:-1;
}
LL exCRT(int n)
{
LL m1,m2,c1,c2,d;
for(int i=2;i<=n;i++)
{
m1=m[i-1],m2=m[i],c1=c[i-1],c2=c[i];
d=gcd(m1,m2);
if((c2-c1)%d)
{
printf("%lld\n",c2-c1);
return -1;
}
m[i] = m[i-1] * m[i] / d;
c[i] = (c2-c1)/d * getInv(m1/d,m2/d) % ( m2 / d ) * m1 + c1;
c[i] = ( c[i] % m[i] + m[i] ) % m[i];
}
return c[n];
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%d%d",&m[i],&c[i]);
printf("%lld",exCRT(n));
return 0;
}例题：
1,2,3,4见上
5. 信封问题
繁难则简：可以得出 D[1]=0,D[2]=1, D[3]=2。
在计算D[n]中，我们先把n提出来，那么1 ~ n - 1中必然有一个k。
分两种情况：
1.k在n的位置上（满足错排）即D[n - 1]
2.k不在n的位置上（为了满足错排），即D[n - 2].
因为k一共有n - 1种选法
故D[n] = (D[n - 1] + D[n - 2]) * (n - 1)，递推求解即可。
6.青蛙的约会
不能简单的认为这是一个追及问题，因为两个青蛙的位移是跳跃性的，不是连续性的，一只青蛙可能从另一只青蛙上“跳”过去，经过而不相遇。
所以我们写下方程式
x+k*m≡y+k*n(modl)
移项：
k* (m−n)−l * z = −(x−y)
令 S = x−y,W = n−m
k * W+l * z = S
用扩展欧几里得：
kj * W+l * zj=(W,l)
（）表示gcd
当gcd(w,l)|S有解
之后，这个方程的所有解就可以表示成
ki=kj+t*L / gcd(W,l)
而因为这个k是建立在exgcd得出的方程上的，方程右边是gcd(W,l)而不是S,所以最后我们需要将结果 * S / gcd(W,L)
