最优贸易(算法竞赛进阶指南)
C 国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市。
任意两个城市之间最多只有一条道路直接相连。
这 m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为 1 条。
C 国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。
但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到 C 国旅游。
当他得知“同一种商品在不同城市的价格可能会不同”这一信息之后,便决定在旅游的同时,利用商品在不同城市中的差价赚一点旅费。
设 C 国 n 个城市的标号从 1∼n,阿龙决定从 1 号城市出发,并最终在 n 号城市结束自己的旅行。
在旅游的过程中,任何城市可以被重复经过多次,但不要求经过所有 n 个城市。
阿龙通过这样的贸易方式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品——水晶球,并在之后经过的另一个城市卖出这个水晶球,用赚取的差价当做旅费。
因为阿龙主要是来 C 国旅游,他决定这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
现在给出 n 个城市的水晶球价格,m 条道路的信息(每条道路所连接的两个城市的编号以及该条道路的通行情况)。
请你告诉阿龙,他最多能赚取多少旅费。
注意:本题数据有加强。
输入格式
第一行包含 2 个正整数 n 和 m,中间用一个空格隔开,分别表示城市的数目和道路的数目。
第二行 n 个正整数,每两个整数之间用一个空格隔开,按标号顺序分别表示这 n 个城市的商品价格。
接下来 m 行,每行有 3 个正整数,x,y,z,每两个整数之间用一个空格隔开。
如果 z=1,表示这条道路是城市 x 到城市 y 之间的单向道路;如果 z=2,表示这条道路为城市 x 和城市 y 之间的双向道路。
输出格式
一个整数,表示答案。
数据范围
1≤n≤100000,
1≤m≤500000,
1≤各城市水晶球价格≤100
输入样例:
5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2
输出样例:
5
这道题的大意就是要我们在1-n中找到最大值和最小值,差即为答案。
第一:这道题是存在环的,转态转移方程行不通。我个人想了个例子
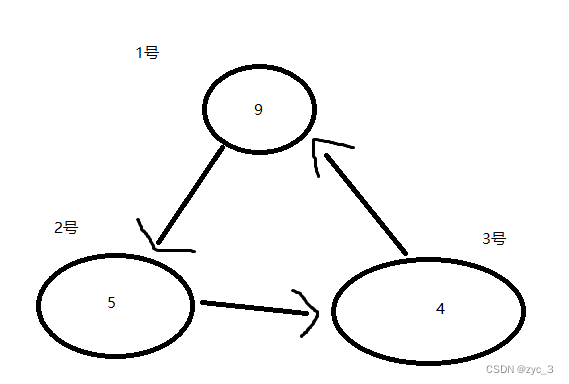
比如在这张图中,我们求什么时候入价最小,d[1] = 9,d[2] = min(5,9) = 5,d[3] = min(5,4) = 4,d[1] = min(4,9) = 4。与开始矛盾,那么d[2] = min(4,5) = 4。事实上,三个点是有区别的。
第二:dijkstra不大行。
dijkstra需要一个最小值,然后用三角不等式收敛,但在本题中
如果当前 dmin[i] 最小的点是 5,那么有可能存在边 5-> 6, 6-> 7, 7-> 5,假设当前 dmin[5] = 10,则有可能存在 6 的价格是11, 但 7 的价格是3,那么 dmin[5] 的值就应该被更新成3,因此当前最小值也不一定是最终最小值,所以dijkstra算法并不适用,我们只能采用 spfa 算法。
从 1 走到 i 的过程中,买入水晶球的最低价格 dmin[i];
从 i走到 n 的过程中,卖出水晶球的最高价格 dmax[i];
1. 为什么要这么想,把i想成一个节点
因为阿龙主要是来 C 国旅游,他决定这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
所以我不可能先卖再买。
dmin[],和dmax[]是解题的关键。是题目条件的变形。那么不难想到,对于每一个中间的节点,我们都要算出dmax[i] - dmin[i]取最大值即为答案。
代码来自:
#include<bits/stdc++.h>
using namespace std;
const int N = 100010, M = 2000010;
int n, m;
int price[N];
int h[N], rh[N], e[M], ne[M], idx;
int dmin[N], dmax[N];
bool st[N];
void add(int *h, int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void spfa(int *d, int start, int *h, bool flag)//这里算最大和最小代码相似,这样可以减少码量
{
queue<int> q;
memset(st, 0, sizeof st);
if (flag) memset(d, 0x3f, sizeof dmin);
q.push(start);
st[start] = true;
d[start] = price[start];
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (flag && d[j] > min(d[t], price[j]) || !flag && d[j] < max(d[t], price[j]))
{
if (flag) d[j] = min(d[t], price[j]);
else d[j] = max(d[t], price[j]);
if (!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
}
/*
上面是常规的spfa的模板,我们先把每一个节点的dmin和dmax算出来
*/
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
memset(rh, -1, sizeof rh);
for (int i = 1; i <= n; i ++ ) scanf("%d", &price[i]);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(h, a, b), add(rh, b, a);
if (c == 2) add(h, b, a), add(rh, a, b);
}
spfa(dmin, 1, h, true);
spfa(dmax, n, rh, false);
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, dmax[i] - dmin[i]);
printf("%d\n", res);
return 0;
}
我们注意到,在代码中,求最大值是n - i 而不是i - n。因为我们不知道从i能否到达n。但我们知道我们一定要到n。于是把n看成起点,就从已知的起点到未知的终点转化成从已知的终点到未知的起点。
详细解释来自:AcWing 341. 最优贸易 - AcWing
如下图所示,1号点能到达3号点,然而3号点却不能走到4号点,若正向从i号点到n号点求出最大价格,以3号点为分界点时,求得的最大差价格是dmax[3] - dmin[3] = 5,然而3号点却到达不了4号点,图中答案是dmax[4] - dmin[4] = 2,因此此做法不可行
因此,从1号点能走到i号点,从n号点走到i号点,则表示从1号点到i号点再到n号点过程中不会发生间断

总结:不必再把spfa看成是求一个点到固定终点的dist,我们通过spfa可以求从任一点到其他点的大部分属性。并且要注意题目的条件,学会反向图。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号