道路与航线（算法竞赛进阶指南）
农夫约翰正在一个新的销售区域对他的牛奶销售方案进行调查。
他想把牛奶送到 T 个城镇，编号为 1∼T。
这些城镇之间通过 R 条道路 (编号为 1 到 R) 和 P 条航线 (编号为 1 到 P) 连接。
每条道路 i 或者航线 i 连接城镇 Ai 到 Bi，花费为 Ci。
对于道路，0≤Ci≤10,000;然而航线的花费很神奇，花费 Ci 可能是负数(−10,000≤Ci≤10,000)。
道路是双向的，可以从 Ai 到 Bi，也可以从 Bi 到 Ai，花费都是 Ci。
然而航线与之不同，只可以从 Ai 到 Bi。
事实上，由于最近恐怖主义太嚣张，为了社会和谐，出台了一些政策：保证如果有一条航线可以从 Ai 到 Bi，那么保证不可能通过一些道路和航线从 Bi 回到 Ai。
由于约翰的奶牛世界公认十分给力，他需要运送奶牛到每一个城镇。
他想找到从发送中心城镇 S 把奶牛送到每个城镇的最便宜的方案。
输入格式
第一行包含四个整数 T,R,P,S。
接下来 R 行，每行包含三个整数（表示一个道路）Ai,Bi,Ci。
接下来 P 行，每行包含三个整数（表示一条航线）Ai,Bi,Ci。
输出格式
第 1..T 行：第 i 行输出从 S 到达城镇 i 的最小花费，如果不存在，则输出 NO PATH。
数据范围
1≤T≤25000,
1≤R,P≤50000,
1≤Ai,Bi,S≤T
输入样例：
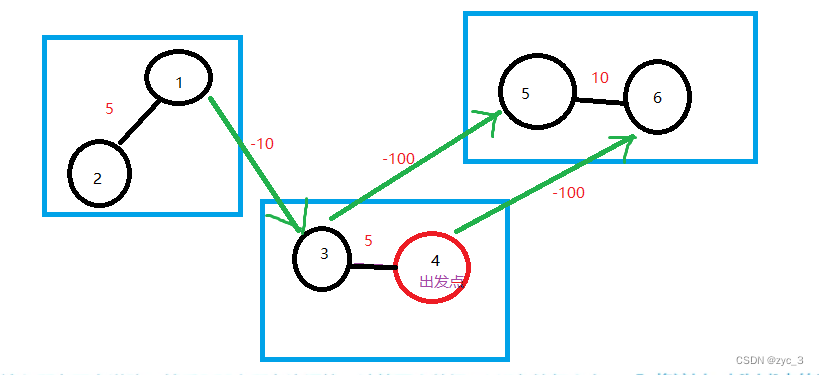
6 3 3 4
1 2 5
3 4 5
5 6 10
3 5 -100
4 6 -100
1 3 -10
输出样例：
NO PATH
NO PATH
5
0
-95
-100
他想找到从发送中心城镇 S 把奶牛送到每个城镇的最便宜的方案。
与其他最短路的题有区别。
这道题我们需要用到拓扑排序
拓扑排序通常用来“排序”具有依赖关系的任务。
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。
这道题我们更新最短路时必须满足这个关系。
连通块处理
图中同时有双向边和单向边。我们可以用连通块来表示出这种关系，使遍历更加方便直观。
个人感觉连通块就是把点分类。
dijkstra
因为是单源最短路。
遍历方向
这道题中我们求的是每个点到起点的距离，所以我们把每个点看成源点，只是统一以出发点为原点进行计算，这样可以保证不漏。
其次，我们为了去重，用上st数组来保证每一个点只能拓展一次，但是可以注意到，一开始我将块内点加入的时候并没有给他们打上vis标记。因此如果他们再次松弛的话还是可以被加入队列。
这样做的原因是因为我们在拓扑排序的基础上，大体上看整个遍历的方向是固定的，不必正着来一遍，再反着来一遍。
由此
图片来源：AcWing 342. 道路与航线 - AcWing
代码来源：AcWing 342. 道路与航线 - AcWing
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N = 25010, M = 150010, INF = 0x3f3f3f3f;
int h[N], e[M], ne[M], w[M], idx;
int dist[N];
bool st[N];
int n, mr, mp, s;
//id:点所在的连通块号, bcnt:连通块数量
int id[N], bcnt;
//连通块的入度数组
int deg[N];
vector<int> block[N];
int q[N], hh, tt = -1;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u)
{
block[bcnt].push_back(u);
id[u] = bcnt;
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(!id[j]) dfs(j);
}
}
void dijkstra(int block_id)
{
priority_queue<PII, vector<PII>, greater<PII>> heap;
//取出该连通块所有的点, 入堆
for(int u : block[block_id])
{
heap.push({dist[u], u});
}
while(heap.size())
{
PII t = heap.top();
heap.pop();
int u = t.second;
if(st[u]) continue;
st[u] = true;
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[u] + w[i])
{
dist[j] = dist[u] + w[i];
if(id[j] == block_id) heap.push({dist[j], j});
}
if(id[j] != block_id && --deg[id[j]] == 0) q[++tt] = id[j];
}
}
}
void topoSort()
{
//dist赋初值
memset(dist, 0x3f, sizeof dist);
dist[s] = 0;
//入度为0的连通块入队列
for(int i = 1; i <= bcnt; i++)
{
if(!deg[i]) q[++tt] = i;
}
while(hh <= tt)
{
int t = q[hh++];
dijkstra(t);
}
}
int main()
{
scanf("%d%d%d%d", &n, &mr, &mp, &s);
memset(h, -1, sizeof h);
for(int i = 0; i < mr; i++)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
//建立所有的连通块
for(int i = 1; i <= n; i++)
{
if(!id[i]) {
++bcnt;
dfs(i);
}
}
//在连通块之间建边
for(int i = 0; i < mp; i++)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), deg[id[b]]++;
}
//算法开始
topoSort();
for(int i = 1; i <= n; i++)
{
if(dist[i] > INF / 2) puts("NO PATH");
else printf("%d\n", dist[i]);
}
return 0;
}
注意事项：
1.对于所有入度为0的连通块，都要加入队列
2.注意最后判定的时候不是dist == inf时才是不连通。因为这个图存在负边（见给的样例图），inf可能会被负边收敛，但仍然是不连通的，所以改成dist >inf / 2
这道题解法不限上述一种。作者水平较差，如有纰漏，欢迎指出。
