树链剖分（含例题）
树链剖分介绍：
图片来自：通俗易懂的树链剖分详解 - 一剑缥缈的洛咕博客 - 洛谷博客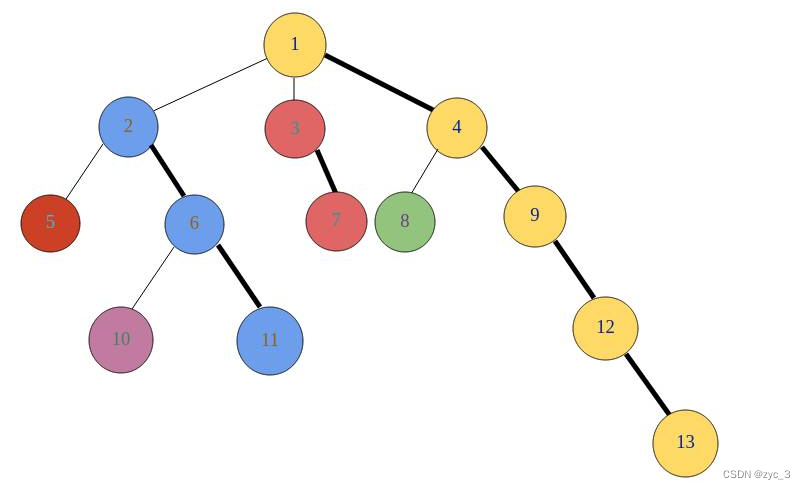
树链剖分的优点：
求LCA中的优化无非就是减少无效搜索的次数，树链剖分把树拆成不同的链（保证不重不漏），因为两个点的LCA一定在一条链上（同一个点），所以如果搜索到的点不在同一条链上，那么不是倍增跳或是······，而是跳过一整条链，这样搜索的速度会大幅提高。
注释代码：
#include<bits/stdc++.h>
using namespace std;
const int N = 500010;
struct edge{
int to,ne;
}edges[1000005];
int n,m,root;
int son[N],size[N],top[N],dep[N],f[N],idx,h[N];
void add(int u,int v)
{
++ idx;
edges[idx].to = v;
edges[idx].ne = h[u];
h[u] = idx;
++ idx;
edges[idx].to = u;
edges[idx].ne = h[v];
h[v] = idx;
}
//size树的大小,dep是点的深度，f是父节点,son是重儿子
void dfs1(int u){
size[u] = 1;
dep[u] = dep[f[u]] + 1;
for(int i = h[u];i;i = edges[i].ne)
{
int v = edges[i].to;
if(v == f[u])continue;
f[v] = u;
dfs1(v);
size[u] += size[v];
if(size[son[u]] < size[v])//求出重儿子
son[u] = v;
}
}
void dfs2(int u,int tp)//tp是链的编号（顶点） ，用于区分不同的链
{
top[u] = tp;
if(son[u])//是重链则一直顺下去，保持链的编号不变
dfs2(son[u],tp);
for(int i = h[u];i;i = edges[i].ne)
{
int v = edges[i].to;
if(v != f[u] && v != son[u])
dfs2(v,v);//重开一条链
}
}
int lca(int u,int v)
{
while(top[u] != top[v])//如果两个点不在同一条链上，直接跳过一整条链
{
if(dep[top[u]] < dep[top[v]])//保持相对大小不变
swap(u,v);
u = f[top[u]];
}
return dep[u] < dep[v] ? u : v;//处于同一条链上，谁跳到上端谁是公共节点
}
int main()
{
int x,y;
cin >> n >> m >> root;
for(int i = 1;i < n;i ++)
{
cin >> x >> y;
add(x,y);
}
dfs1(root);
dfs2(root,root);
for(int i = 1;i <= m;i ++)
{
cin >> x >> y;
cout << lca(x,y) << endl;
}
}T4烤乐滋野餐
题目介绍：
解题思路：
这道题为什么跟LCA有关系呢？
首先看题目数据，n个点，n - 1条边，那么图大概是这个形状：
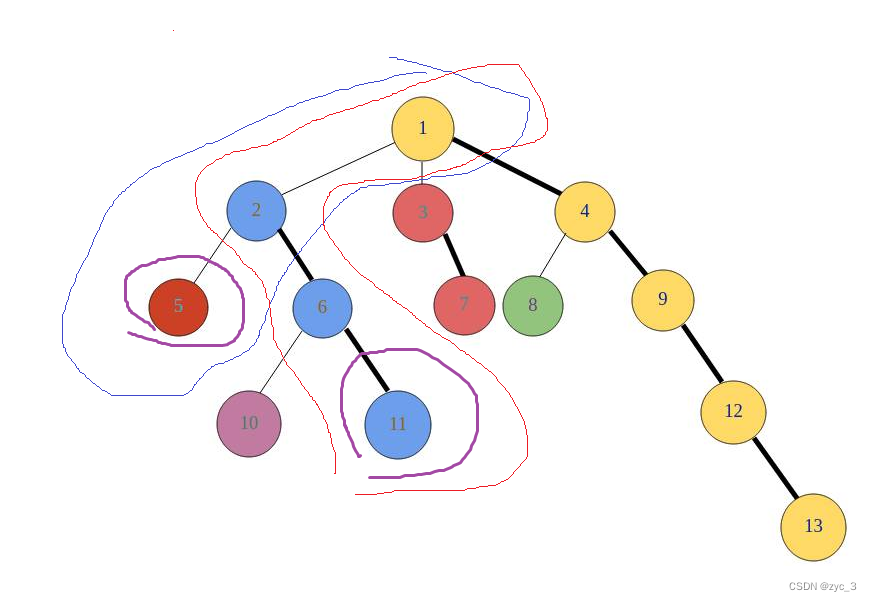
题中给定两个点，求这两个点经过的距离和（默认要小），两个点的食物和。
显然，我们可以看到只是求图中关于这两个点的局部。（在上图中，画紫色圈的是x,y），那么我们肉眼可确立路径，5,2,6,11。
我们必然要找LCA作为“拐点”，同时利用树链剖分的性质结合容斥原理，可以快速计算出距离和以及食物和。
1.5,2,6,11的距离和可以看成蓝条 + 红条 - （1,2） - （1）。
对应代码：
ans1=val[x]+val[y]-val[LCA]-val[fa[LCA]]val是如此得出的
void dfs1(int now,int fath,int diss,int var)//now是当前这个点,fath是父节点,diss(dis)是距离和,var是食物的和
{
fa[now]=fath;dep[now]=dep[fath]+1;
sz[now]=1;dis[now]=diss;
val[now]=var;
for(int i=head[now];i;i=nxt[i])
{
int v=to[i];
if(v==fath)
continue;
dfs1(v,now,diss+w[i],var+va[v]);
sz[now]+=sz[v];
if(sz[v]>sz[son[now]])
son[now]=v;
}
}2.同理，距离和更好算
在上图中：5 - 2的距离即为dis[x] - dis[LCA],2 - 11 的距离即为dis[y] - dis[LCA]
对应代码：ans2=dis[x]+dis[y]-2*dis[LCA]
可以发现，上述两个结论具有普遍意义。
于是，我们用树链剖分 + 类似前缀和 得到了更加高效的计算方式。
完整代码
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int N=200005;
int to[N],head[N],nxt[N],w[N],cnt;
void add(int u,int v,int wi)
{
to[++cnt]=v;
nxt[cnt]=head[u];
w[cnt]=wi;
head[u]=cnt;
}
int dep[N],top[N],sz[N],fa[N],son[N];
int dis[N],val[N],va[N];//va表示食物的数量
/*
dfs1,dfs2,lca树链剖分
*/
void dfs1(int now,int fath,int diss,int var)//now是当前这个点,fath是父节点,diss(dis)是距离和,var是食物的和
{
fa[now]=fath;dep[now]=dep[fath]+1;
sz[now]=1;dis[now]=diss;
val[now]=var;
for(int i=head[now];i;i=nxt[i])
{
int v=to[i];
if(v==fath)
continue;
dfs1(v,now,diss+w[i],var+va[v]);
sz[now]+=sz[v];
if(sz[v]>sz[son[now]])
son[now]=v;
}
}
void dfs2(int now,int t)
{
top[now]=t;
if(!son[now])
return;
dfs2(son[now],t);
for(int i=head[now];i;i=nxt[i])
{
int v=to[i];
if(v==fa[now]||v==son[now])
continue;
dfs2(v,v);
}
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
x=fa[top[x]];
}
return dep[x]>dep[y]?y:x;
}
int n,q;
int gcd(int a,int b)
{
if(a==0)
swap(a,b);
return b==0?a:gcd(b,a%b);//辗转相除法，模板很多种
}
int main()
{
n=read();
for(int i=1;i<=n;i++)
va[i]=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read(),wi=read();
add(u,v,wi);add(v,u,wi);
}
dfs1(1,0,0,va[1]);
dfs2(1,1);
q=read();
while(q--)
{
int x=read(),y=read();
int LCA=lca(x,y);
int ans1=val[x]+val[y]-val[LCA]-val[fa[LCA]],ans2=dis[x]+dis[y]-2*dis[LCA];//见博客
int GCD=gcd(ans1,ans2);
printf("%d/%d\n",ans1/GCD,ans2/GCD);
}
return 0;
}
