[NOIP2013 提高组] 火柴排队

[NOIP2013 提高组] 火柴排队

题目描述

涵涵有两盒火柴，每盒装有 $n$ 根火柴，每根火柴都有一个高度。 现在将每盒中的火柴各自排成一列， 同一列火柴的高度互不相同， 两列火柴之间的距离定义为：$ \sum (a_i-b_i)^2$

其中 $a_i$ 表示第一列火柴中第 $i$ 个火柴的高度，$b_i$ 表示第二列火柴中第 $i$ 个火柴的高度。

每列火柴中相邻两根火柴的位置都可以交换，请你通过交换使得两列火柴之间的距离最小。请问得到这个最小的距离，最少需要交换多少次？如果这个数字太大，请输出这个最小交换次数对 $10^8-3$ 取模的结果。

输入格式

共三行，第一行包含一个整数 $n$，表示每盒中火柴的数目。

第二行有 $n$ 个整数，每两个整数之间用一个空格隔开，表示第一列火柴的高度。

第三行有 $n$ 个整数，每两个整数之间用一个空格隔开，表示第二列火柴的高度。

输出格式

一个整数，表示最少交换次数对 $10^8-3$ 取模的结果。

样例 #1

样例输入 #1

4
2 3 1 4
3 2 1 4

样例输出 #1

1

样例 #2

样例输入 #2

4
1 3 4 2
1 7 2 4

样例输出 #2

2

提示

【输入输出样例说明一】

最小距离是 0，最少需要交换 1 次，比如：交换第 1 列的前 2 根火柴或者交换第 2 列的前 2根火柴。

【输入输出样例说明二】

最小距离是 10，最少需要交换 2 次，比如：交换第 1 列的中间 2 根火柴的位置，再交换第 2 列中后 2根火柴的位置。

【数据范围】

对于 $10\%$ 的数据， $1\le n\le 10$；

对于 $30\%$ 的数据，$1\le n\le 100$；

对于 $60\%$ 的数据，$1\le n\le 10^3$；

对于 $100\%$ 的数据，$1\le n\le 10^5$，$0\le$ 火柴高度 $<2^{31}$。

题解

首先得出，a数列中第几大的数和b数列中第几大的数要上下对应。

也就是说我们要以一行位模板串，以它的排序方式为规则，所以要用到数组q，以a[i]为关键字对b排序。

这里是以b[i]为关键字对a排序的，当两个序列相同时，比如当i = 1时，c[b[i]] = a[i]。
也就是c数组的下标和数值相等，代表a[i] = b[i]。当c数组出现逆序对的时候，说明有a[i]!=b[i]。
把要比较的两个量放在一个数组里，利用逆序对的方式去计算有几个数据不同是这题的特性

我们存一个数组c[i];
 c[B[i]编号]=A[i]编号；
 A：2 3 1 4->1 2 3 4对应原编号为：3 1 2 4
 B：3 2 1 4->1 2 3 4对应原编号为：3 2 1 4
 c[B[1]编号]=c[3]=a[1]编号=3
 c[B[2]编号]=c[2]=a[2]编号=1
 c[B[3]编号]=c[1]=a[3]编号=2
 c[B[4]编号]=c[4]=a[4]编号=4
 于是c[1]=2 c[2]=1 c[3]=3 c[4]=4
 逆序对数=1，交换一次。

$问题转化为求c数组中逆序对的个数$

题目要求相邻交换，用归并排序 $or$（树状排序）来算逆序对的个数。

在此之前，观察到数据范围比较大，要用离散化压缩一下空间。

归并排序

#include<bits/stdc++.h>
 using namespace std;
 typedef struct n{
   int num,ord;
 }node;
 node first_team[100010],second_team[100010];
 int a[100010],b[100010],ans;
 int compare(node x,node y)
 {
   return x.num < y.num;
 }
 void Merge(int l,int r)
 {
   if(l>=r) return ;
   int mid=(l+r)/2;
   Merge(l,mid);
   Merge(mid+1,r);
   int i=l,j=mid+1,k=l;
   while(i<=mid&&j<=r)
   {
     if(a[i]>a[j])
     {
       b[k++]=a[j++];
       ans+=mid-i+1;
       ans%=99999997;
     }
     else b[k++]=a[i++];
   }
   while(i<=mid) b[k++]=a[i++];
   while(j<=r) b[k++]=a[j++];
   for(int i=l;i<=r;i++)
     a[i]=b[i];
 }
 int main()
 {
   int n;
   scanf("%d",&n);
   for(int i=1;i<=n;i++)
   {
     scanf("%d",&first_team[i].num);
     first_team[i].ord=i;
   }
   for(int i=1;i<=n;i++)
   {
     scanf("%d",&second_team[i].num);
     second_team[i].ord=i;
   }
   sort(first_team+1,first_team+n+1,compare);
   sort(second_team+1,second_team+n+1,compare);
   for(int i=1;i<=n;i++)
     a[first_team[i].ord]=second_team[i].ord;
   Merge(1,n);
   printf("%d",ans);
   return 0;
 }

树状数组

解释

树状数组就是维护区间和的一种解法，因为本题要知道在一个数前面有多少数能与它组成逆序对，所以适应树状数组的特性。

图片解释来自https://www.luogu.com.cn/blog/ryoku/solution-p1908

6

5 4 2 6 3 1

1)进行离散化操作，处理数据（这里储存的是在数组中是第几大的）：a[]={2,3,5,1,4,6}

2)然后加入a1 = 2,(即2的位置上放了一个数) ，ans=0，目前数组中小于a1的全部可以和a1组成逆序对

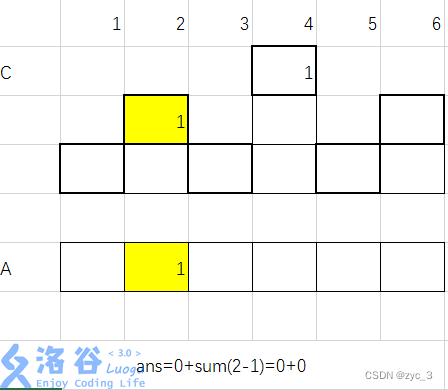
3)加入 a2=3 ans=1 同上

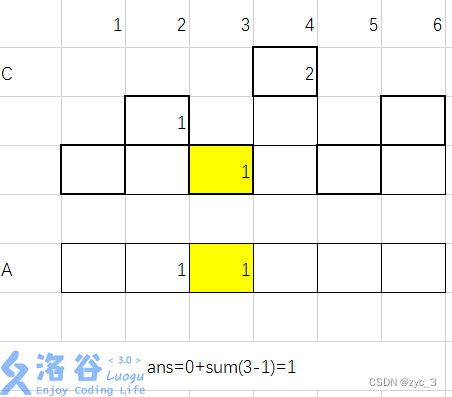
4)加入 a3=5 ans=3

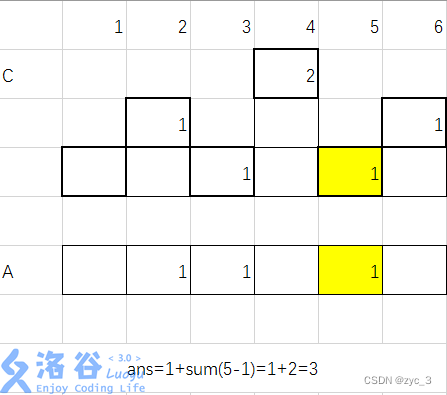
5)加入 a4=1 ans=3

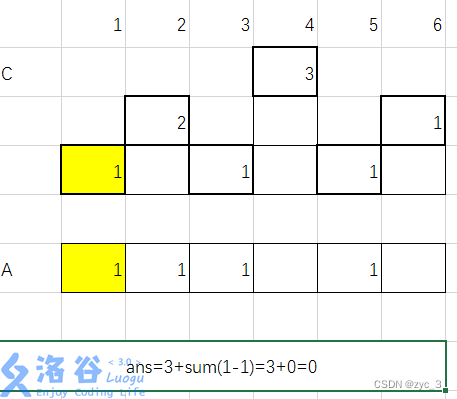
6)加入 a5=4 ans=6

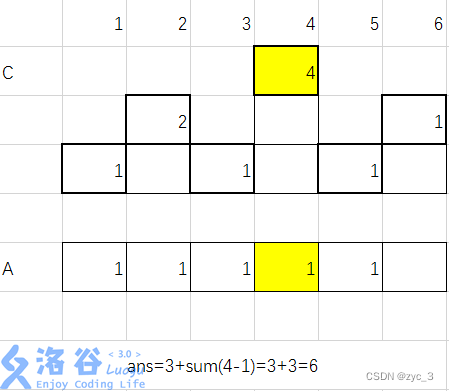
6)加入 a6=6 ans=11

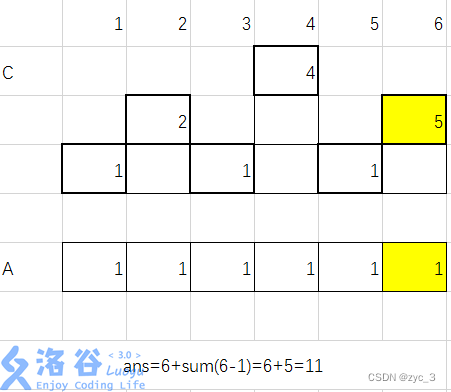
树状数组求逆序对的模板，也是来自同一作者

#include<algorithm>
#include<cstdio>
using namespace std;
int n,m,c[40005]={0},a[40005]={0},b[40005]={0};  //定义数组，b[]为读入的数组，a[]为要离散化后的数组，C[]为树状数组
inline void Add(register int x)  //树状数组加入
{
    for(;x<=n;x+=(x&-x))
        c[x]++;  //因为这里只需要1，所以我就写出c[x]++了
}
inline int Sum(register int x)  //树状数组求和，同上面的sum(x)
{
    register int s=0;  //计数的变量
    for(;x>0;x-=(x&-x))  //累计
        s+=c[x];
    return s;  //返回结果
}
bool cmp1(const int &x,const int &y)  //离散化需要用的，上面有讲
{
    return b[x]>b[y];
}
int main()
{
    int ans=0;  //ans为最后的结果
    scanf("%d",&n);  //读入n
    for(register int i=1;i<=n;i++)
    {
        scanf("%d",&b[i]);  //读入
        a[i]=i;  //顺便初始化一下a数组
    }
    sort(a+1,a+n+1,cmp1);  //给a数组排序，达到最终的效果
    for(register int i=1;i<=n;i++)
    {
        Add(a[i]);  //依次加入树状数组
        ans+=Sum(a[i]-1);  //计算结果并累计
    }
    printf("%d",ans);  //输出ans
    return 0;  //返回
}

关于本题的代码：

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 100010;
const int maxm = 99999997;
struct MyStruct
{
    int data;
    int loc;
}a[maxn],b[maxn];
int e[maxn], n, c[maxn];
int inline readint()
{
    int x = 0;
    char c = getchar();
    while (c<'0' || c>'9') c = getchar();
    while (c >= '0'&&c <= '9')
    {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x;
}
int lowbit(int x)
{
    return x&-x;//树状数组实现 
}
void add(int x,int t)
{
    while (x <= n)
    {
        e[x] += t;
        e[x] %= maxm;
        x += lowbit(x);//每次往后加，可以改变后面对应的和 
    }
}
int sum(int x)
{
    int s = 0;
    while(x)
    {
        s += e[x];
        s %= maxm;
        x -= lowbit(x);//得到所求的和 
    }
    return s;
}
bool cmp(MyStruct x, MyStruct y)
{
    return x.data < y.data;
}
int main()
{
    n = readint();
    for (int i = 1; i <= n; i++)
    {
        a[i].data = readint();
        a[i].loc = i;//记录位置 
    }
    for (int i = 1; i <= n; i++)
    {
        b[i].data = readint();
        b[i].loc = i;
    }
    sort(a + 1, a + n + 1, cmp);
    sort(b + 1, b + n + 1, cmp);
    for (int i = 1; i <= n; i++)
    {
        c[a[i].loc] = b[i].loc;//离散优化 
    }
    int ans = 0;
    for (int i = 1; i <= n; i++)
    {
        add(c[i], 1);//离散优化后大小就是正确顺序的位置 
        ans += i - sum(c[i]);/*
    i是a的当前位置，sum(c[i])表示c[i]前有几个位置(c[i]应该排在第几个位置）差即为要移动的位置	
	举例：i = 1
	c[i] = 5,sum(5) = 1,i - sum(5) = 0.   5 3 2 1 4
	i = 2
	c[i] = 3,sum(3) = 1,i - sum(3) = 1.   3 5 2 1 4
	i = 3
	c[i] = 2,sum(2) = 1,i - sum(2) = 2.   2 3 5 1 4
	i = 4
	c[i] = 1,sum(1) = 1,i - sum(1) = 3.   1 2 3 5 4
	i = 5
	c[i] = 1,sum(c[i]) = 4,i - sum(c[i]) = 1. 1 2 3 4 5
	移动火柴有一定的规则
        要将下面的逆序对全部消除应该怎么移动：
        5 4 1 2 3
        5 1 4 2 3
        1 5 4 2 3
      	1 5 2 4 3
      	1 2 5 4 3
      	1 2 5 3 4
      	1 2 3 5 4
      	1 2 3 4 5
      	由上面的过程可以发现对于每一个小的数，我们都要把他提上来，提的次数取决于它的前面有几个数比他大，和移动火柴的限制要求恰好相似。
  
	*/
        ans %= maxm;
    }
    printf("%d", ans);
    return 0;
}

每次+ 或 *都要取模。