CSPS2021回文
[CSP-S 2021] 回文
题目描述
给定正整数 \(n\) 和整数序列 \(a_1, a_2, \ldots, a_{2 n}\)，在这 \(2 n\) 个数中，\(1, 2, \ldots, n\) 分别各出现恰好 \(2\) 次。现在进行 \(2 n\) 次操作，目标是创建一个长度同样为 \(2 n\) 的序列 \(b_1, b_2, \ldots, b_{2 n}\)，初始时 \(b\) 为空序列，每次可以进行以下两种操作之一：
- 将序列 \(a\) 的开头元素加到 \(b\) 的末尾，并从 \(a\) 中移除。
- 将序列 \(a\) 的末尾元素加到 \(b\) 的末尾，并从 \(a\) 中移除。
我们的目的是让 \(b\) 成为一个回文数列，即令其满足对所有 \(1 \le i \le n\)，有 \(b_i = b_{2 n + 1 - i}\)。请你判断该目的是否能达成，如果可以，请输出字典序最小的操作方案，具体在【输出格式】中说明。
输入格式
每个测试点包含多组测试数据。
输入的第一行，包含一个整数 \(T\)，表示测试数据的组数。对于每组测试数据：
第一行，包含一个正整数 \(n\)。
第二行，包含 \(2 n\) 个用空格隔开的整数 \(a_1, a_2, \ldots, a_{2 n}\)。
输出格式
对每组测试数据输出一行答案。
如果无法生成出回文数列，输出一行 ‐1，否则输出一行一个长度为 \(2 n\) 的、由字符 L 或 R 构成的字符串（不含空格），其中 L 表示移除开头元素的操作 1，R 表示操作 2。
你需要输出所有方案对应的字符串中字典序最小的一个。
字典序的比较规则如下：长度均为 \(2 n\) 的字符串 \(s_{1 \sim 2 n}\) 比 \(t_{1 \sim 2 n}\) 字典序小，当且仅当存在下标 \(1 \le k \le 2 n\) 使得对于每个 \(1 \le i < k\) 有 \(s_i = t_i\) 且 \(s_k < t_k\)。
样例 #1
样例输入 #1
2
5
4 1 2 4 5 3 1 2 3 5
3
3 2 1 2 1 3
样例输出 #1
LRRLLRRRRL
-1
样例 #2
样例输入 #2
见附件中的 palin/palin2.in
样例输出 #2
见附件中的 palin/palin2.ans
提示
【样例解释 #1】
在第一组数据中，生成的的 \(b\) 数列是 \([4, 5, 3, 1, 2, 2, 1, 3, 5, 4]\)，可以看出这是一个回文数列。
另一种可能的操作方案是 LRRLLRRRRR，但比答案方案的字典序要大。
【数据范围】
令 \(\sum n\) 表示所有 \(T\) 组测试数据中 \(n\) 的和。
对所有测试点保证 \(1 \le T \le 100\)，\(1 \le n, \sum n \le 5 \times {10}^5\)。
| 测试点编号 | \(T \le\) | \(n \le\) | \(\sum n \le\) | 特殊性质 |
|---|---|---|---|---|
| \(1 \sim 7\) | \(10\) | \(10\) | \(50\) | 无 |
| \(8 \sim 10\) | \(100\) | \(20\) | \(1000\) | 无 |
| \(11 \sim 12\) | \(100\) | \(100\) | \(1000\) | 无 |
| \(13 \sim 15\) | \(100\) | \(1000\) | \(25000\) | 无 |
| \(16 \sim 17\) | \(1\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | 无 |
| \(18 \sim 20\) | \(100\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | 有 |
| \(21 \sim 25\) | \(100\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | 无 |
特殊性质：如果我们每次删除 \(a\) 中两个相邻且相等的数，存在一种方式将序列删空（例如 \(a = [1, 2, 2, 1]\)）。
【hack 数据提供】
@潜在了H2O下面。
解答
这道题是一个很好的思维题。我看出两个性质：
- 第一个必然是L
- 最后一个必然是L
不会了，但猜到了是栈，没想到用两个栈
看过题解后：
- 为什么要用两个栈，我们可以想到可以第一个数和数列中与之相同的数的位置作为两个断点。
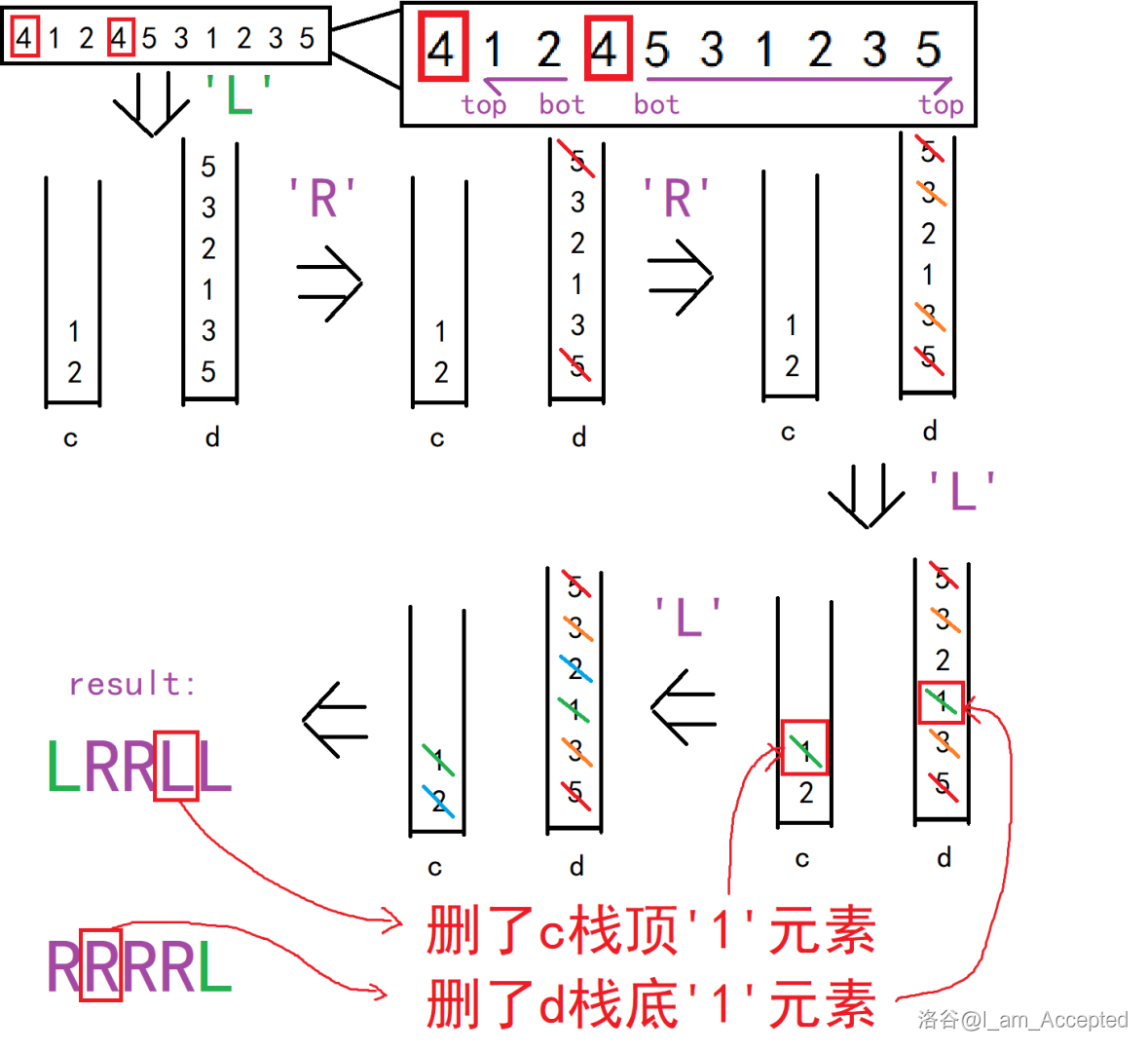
借犇犇一个图
-
根据题目的意思，我们可以删数列的左边，也可以删右边。因为一开始两个断点一个是第一个放进去的，另个一个是最后一个放进去的，已经固定了。那么我们要做的就是先删里面的，再删外面的，所以对应的两个栈分别是由上到下和由下到上。
-
我们可以发现两个栈空的时候出答案
-
什么时候可以删数呢？回归题目，第一个数列可以从左往右删，因为第二个断点已经把右边锁死了，第二个数列可以从右往左删，对应的就是1的栈顶，2的栈底。我们还可以发现，假如两个相同的数分别存在于一个栈的栈顶和栈底，也是可以删的。
-
删数时如何保存答案？可以看图，然后你要发现，一个L对应一个R，R还是对应R，因为如果你在答案前半行有R的话，说明那属于4中第二种情况，对应的也是R，L就不说了（错误结论，留来警示自己的zz）
-
首先第一个数和最后一个数是不用算进去的，那么我们要清空2*(n-1),如果此时算到第i个数，那么就是2 * (n-1) - i就可以得到右端点？因为我们在最终的结果中是算上第一个数的，所以还要向右平移一位。答案为2 * (n-1) - i +1
代码
手写错误代码。
#include<bits/stdc++.h>
#define rt register int
using namespace std;
int T,n,cnt;
char s[1000005];
int a[1000005];
deque<int> q1,q2;
int main()
{
scanf("%d",&T);
while(T--){
scanf("%d",&n);
n=n*2;
s[1]='L';
s[n]='L';
for(rt i=1;i<=n;++i)
scanf("%d",&a[i]);
int x0=a[1];
int y0;
cnt=1;
for(rt i=1;i<=n;++i)
if(a[i]==x0)y0=i;
for(rt i=2;i<y0;++i)
q1.push_back(a[i]);
for(rt i=y0+1;i<=n;++i)
q2.push_front(a[i]);
int a=q1.size(),b=q2.size();
while(!q1.empty()||!q2.empty())
{
if(q1.front()==q2.back()){
s[++cnt]='L';
q1.pop_front();
q2.pop_back();
}else if(q2.front()==q2.back())
{
s[++cnt]='R';
q2.pop_front();
q2.pop_back();
}
if(q1.size()==a&&q2.size()==b)break;
a=q1.size();b=q2.size();
cout<<a<<" "<<b<<endl;
}
if(!q1.empty()&&!q2.empty()){printf("-1\n");continue;}
else {
for(rt i=1;i<n/2;++i)
s[i+n/2]='R';
for(rt i=1;i<=n;++i)printf("%c ",s[i]);
puts("");
}
}
return 0;
}
错在两处，一个是忽略了开头是R的情况，具体可见
-
20
17 3 16 1 9 12 19 6 8 2 20 14 18 10 5 11 15 7 13 4 4 13 7 15 11 5 10 18 17 14 20 2 8 6 19 12 9 1 16 3
答案为
RRRRRRRRRRRRRRRRRRRRRRRRRRRRLRRRRRRRRRRL
其实左右的性质是对称的，这个是不用说明的，但是受到每个数的位置不是左右对称的，所以还要算以R开头的情况。
-
那个sb说L就一定对应R了，吃错药了。详见解答6
正解：来自不同犇犇
#include<bits/stdc++.h>
using namespace std;
#define rt register int
int n,T;
char res[1000005];
int a[1000005];
inline bool work(int l1,int r1,int l2,int r2) {
for(rt i=1;i<n;++i) {
if(l1<=r1&&((l2<=r2&&a[l1]==a[l2])||(l1<r1&&a[l1]==a[r1]))) {
if(l1<r1&&a[l1]==a[r1]) {
++l1; --r1;
res[i]='L'; res[2*(n-1)-i+1]='L';
}
else {
++l1; ++l2;
res[i]='L'; res[2*(n-1)-i+1]='R';
}
}
else if(l2<=r2&&((l1<=r1&&a[r2]==a[r1])||(l2<r2&&a[l2]==a[r2]))) {
if(l2<r2&&a[l2]==a[r2]) {
++l2; --r2;
res[i]='R'; res[2*(n-1)-i+1]='R';
}
else {
--r2; --r1;
res[i]='R'; res[2*(n-1)-i+1]='L';
}
}
else {return 0;}
}
return 1;
}
int main() {
scanf("%d",&T);
while(T--) {
scanf("%d",&n);int p1=-1,p2=-1;
for(rt i=1;i<=2*n;++i) scanf("%d",&a[i]);
for(rt i=1;i<=2*n+1;++i) res[i]=0;
for(rt i=2;i<=2*n;++i) {if(a[1]==a[i]) {p1=i; break;}}
for(rt i=1;i<2*n;++i) {if(a[2*n]==a[i]) {p2=i; break;}}
if(work(2,p1-1,p1+1,2*n)) {printf("L%sL\n",res+1);}
else if(work(1,p2-1,p2+1,2*n-1)) {printf("R%sL\n",res+1);}
else {printf("-1\n");}
}
return 0;
}
