基础数论
P3383 【模板】线性筛素数
快速幂
裴蜀定理
裴蜀定理得名于法国数学家艾蒂安·裴蜀,说明了对任何整数a、b和它们的最大公约数d,关于未知数x和y的线性丢番图方程(称为裴蜀等式): ax + by = m 有解当且仅当m是d的倍数。
求逆元:
逆元的意义就是在%的运算中把除法转换为乘法
扩展欧几里得:
ax+by=c
x′=x0∗c/d,y′=y0∗c/d
应用: 求解一次同余方程 ax≡b(modm)则等价于求
ax=m∗(−y)+b//从%的定义出发
ax+my=b
有解条件为gcd(a,m)|b,然后用扩展欧几里得求解即可
特殊情况 当 b=1且 a与m互质时 则所求的x即为a的逆元
快速幂:配合费马小定理
若p为素数,a为正整数,且a、p互质。
则有a^(p−1)≡1(mod p)
a∗x≡1(mod p)
a∗x≡a^(p−1)(mod p)
x≡a^(p−2)(mod p)
所以我们可以用快速幂来算出 ap−2(modp)ap−2(modp)的值,这个数就是它的逆元了
线性算法:
前置:
首先我们有一个,1^−1≡1(mod p)
然后设 p=k∗i+r,(1<r<i<p) 也就是 k 是 p/i的商,r 是余数 。
再将这个式子放到(mod p)意义下就会得到:
k∗i+r≡0(mod p)
PS:(-p/i+p)防止负数
线性求组合数
这里直接贴卢卡斯定理的例题,题目在洛谷P3807
扩展中国剩余定理
例题洛谷P4777 题解区第一篇有很好的解释
例题:
1.
2.
3.
4.
5.
6.
7.
1,2,3,4见上
5. 信封问题
繁难则简:可以得出 D[1]=0,D[2]=1, D[3]=2。
在计算D[n]中,我们先把n提出来,那么1 ~ n - 1中必然有一个k。
分两种情况:
1.k在n的位置上(满足错排)即D[n - 1]
2.k不在n的位置上(为了满足错排),即D[n - 2].
因为k一共有n - 1种选法
故D[n] = (D[n - 1] + D[n - 2]) * (n - 1),递推求解即可。
6.青蛙的约会
不能简单的认为这是一个追及问题,因为两个青蛙的位移是跳跃性的,不是连续性的,一只青蛙可能从另一只青蛙上“跳”过去,经过而不相遇。
所以我们写下方程式
x+k*m≡y+k*n(modl)
移项:
k* (m−n)−l * z = −(x−y)
令 S = x−y,W = n−m
k * W+l * z = S
用扩展欧几里得:
kj * W+l * zj=(W,l)
()表示gcd
当gcd(w,l)|S有解
之后,这个方程的所有解就可以表示成
ki=kj+t*L / gcd(W,l)
而因为这个kk是建立在exgcdexgcd得出的方程上的,方程右边是gcd(W,l)gcd(W,l)而不是SS,所以最后我们需要将结果 * S / gcd(W,L)
7.分特产
详见
本文作者:zychh
本文链接:https://www.cnblogs.com/zychh/p/16591180.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。

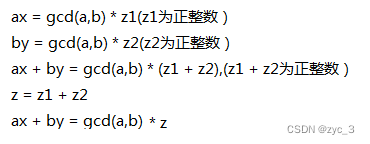






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步