HDU 5245 Joyful（期望）

 http://acm.hdu.edu.cn/showproblem.php?pid=5245

题意：

给出一个n*m的矩阵格子，现在有k次操作，每次操作随机选择两个格子作为矩形的对角，然后将这范围内的格子填色，现在要求经过k次操作后填色格子的期望值。

 

思路：

给个格子都是独立的，所以只需要计算出每个格子经过k次操作后被填色的概率即可，最后所有格子相加就是期望值。但是直接求填色概率不好求，求不被填色概率会比较容易。假设一次操作的不被填色概率为p，那么k次之后的概率为p^k，最后该格子填色概率就是1-p^k。

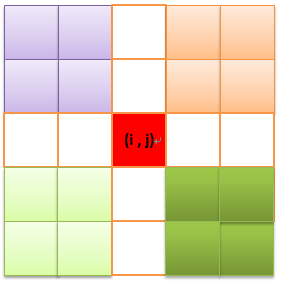
如图所示，假设我们现在要求（i，j）这个格子的不被填色概率，那么我们可以选择的两个格子可以是上部，左部，右部和下部，但是这样的话对角的四个矩形区域重复计算了一次，所以需要减去。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
int m,n,k;

int main()
{
    //freopen("in.txt","r",stdin);
    int T;
    scanf("%d",&T);
    int cas = 1;
    while(T--)
    {
        scanf("%d%d%d",&n,&m,&k);
        double ans = 0;
        double sum = (ll)m*n*m*n;
        for(ll i=1;i<=n;i++)
        {
            for(ll j=1;j<=m;j++)
            {
                ll num = 0;
                num += (i-1)*m*(i-1)*m;  //上
                num += (n-i)*m*(n-i)*m;  //下
                num += (j-1)*n*(j-1)*n;  //左
                num += (m-j)*n*(m-j)*n;  //右
                num -= (i-1)*(j-1)*(i-1)*(j-1);
                num -= (i-1)*(m-j)*(i-1)*(m-j);
                num -= (n-i)*(j-1)*(n-i)*(j-1);
                num -= (n-i)*(m-j)*(n-i)*(m-j);
                ans += 1 - pow(num/sum, k);
            }
        }
        int a = round(ans);
        printf("Case #%d: %d\n",cas++, a);
    }
    return 0;
}