BZOJ 1010: [HNOI2008]玩具装箱toy（斜率优化dp）

http://www.lydsy.com/JudgeOnline/problem.php?id=1010

题意：

 

思路：

容易得到朴素的递归方程：$dp(i)=min(dp(i),dp(k)+(i-k-1+sum[i]-sum[k]-l)^{2})$，$sum[i]$表示前i个玩具的$c_{i}$之和。$f(k)$表示前k个玩具的最小费用。

如果设$f(i)=sum[i]+i$，那么上式就可以改写为$dp(i)=min(dp(i),dp(k)+(f(i)-f(k)-l-1)^{2})$。

所以这道题目是很明显的斜率优化dp。

 

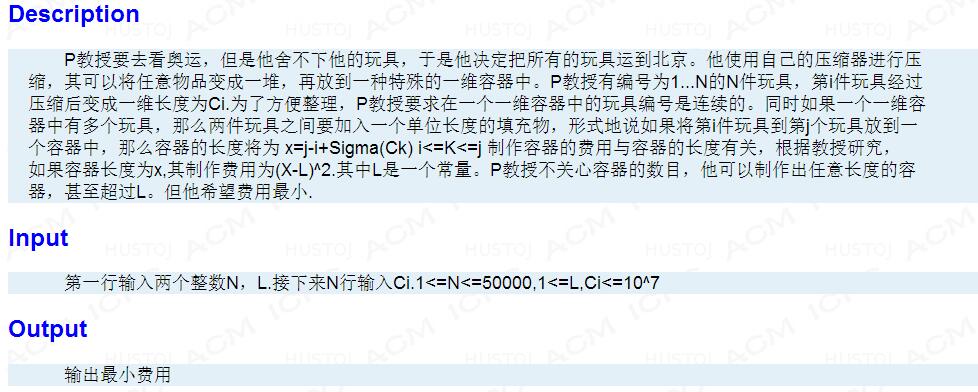
如果k决策比j决策更优的话，那么（c=l+1）

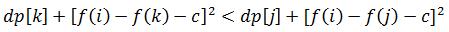
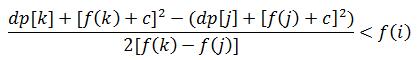
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<sstream>
#include<vector>
#include<stack>
#include<queue>
#include<cmath>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
typedef pair<int,ll> pll;
const int INF = 0x3f3f3f3f;
const int maxn=50000+5;

ll n, l;
ll c[maxn];
ll dp[maxn];
ll sum[maxn];
ll Q[maxn];

ll dy(ll k, ll j)
{
    return dp[k]+(sum[k]+l)*(sum[k]+l)-dp[j]-(sum[j]+l)*(sum[j]+l);
}

ll dx(ll k, ll j)
{
    return 2*(sum[k]-sum[j]);
}

int main()
{
    //freopen("in.txt","r",stdin);
    while(~scanf("%lld%lld",&n,&l))
    {
        l+=1;
        sum[0]=0;
        for(int i=1;i<=n;i++)
        {
            scanf("%I64d",&c[i]);
            sum[i]=sum[i-1]+c[i];
        }
        for(int i=1;i<=n;i++)  sum[i]+=i;
        Q[1]=0;
        int frt=1,rear=1;
        for(int i=1;i<=n;i++)
        {
            while(frt<rear && dy(Q[frt+1],Q[frt])<=sum[i]*dx(Q[frt+1],Q[frt]))   frt++;
            int tmp=Q[frt];
            dp[i]=dp[tmp]+(sum[i]-sum[tmp]-l)*(sum[i]-sum[tmp]-l);
            while(frt<rear && dy(Q[rear],Q[rear-1])*dx(i,Q[rear])>=dy(i,Q[rear])*dx(Q[rear],Q[rear-1]))  rear--;
            Q[++rear]=i;
        }
        printf("%lld\n",dp[n]);
    }
    return 0;
}