BZOJ 1003: [ZJOI2006]物流运输（spfa+dp）

http://www.lydsy.com/JudgeOnline/problem.php?id=1003

题意：

 

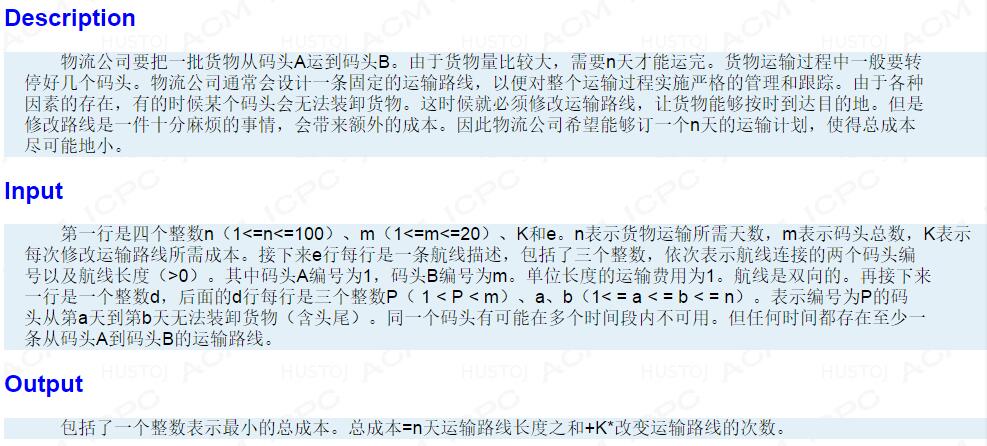
思路：

首先用spfa计算一下任意两天之内的最短路，dis[a][b]表示的就是在第a天~第b天从1到m的最短路。

接下来就是dp了，f[i]表示前i天的最小代价，那么状态转移方程就是：

f[i]=min(f[i],f[j]+dis[j+1][i]*(i-j)+k)

注意：边界条件f[0]=-k！

 

  1 #include<iostream>
  2 #include<algorithm>
  3 #include<cstring>
  4 #include<cstdio>
  5 #include<sstream>
  6 #include<vector>
  7 #include<stack>
  8 #include<queue>
  9 #include<cmath>
 10 #include<map>
 11 #include<set>
 12 using namespace std;
 13 typedef long long ll;
 14 typedef pair<int,ll> pll;
 15 const int INF = 0x3f3f3f3f;
 16 const int maxn=1000+5;
 17 
 18 int n, m, k, t;
 19 int tot;
 20 int head[maxn];
 21 int flag[maxn][maxn];
 22 int dis[maxn][maxn];
 23 int d[maxn];
 24 int inq[maxn];
 25 ll f[maxn];
 26 
 27 struct node
 28 {
 29     int v, w;
 30     int next;
 31 }e[maxn];
 32 
 33 void AddEdge(int u, int v, int w)
 34 {
 35     e[tot].v=v;
 36     e[tot].w=w;
 37     e[tot].next=head[u];
 38     head[u]=tot++;
 39 }
 40 
 41 void spfa(int s, int a, int b)
 42 {
 43     for(int i=1;i<=m;i++)   d[i]=INF;
 44     queue<int> Q;
 45     Q.push(s);
 46     d[s]=0;
 47     while(!Q.empty())
 48     {
 49         int u=Q.front(); inq[u]=0; Q.pop();
 50         for(int i=head[u];i!=-1;i=e[i].next)
 51         {
 52             int v=e[i].v;
 53             if(flag[v][b]-flag[v][a-1]>0)  continue;
 54             if(d[v]>d[u]+e[i].w)
 55             {
 56                 d[v]=d[u]+e[i].w;
 57                 if(!inq[v])
 58                 {
 59                     Q.push(v);
 60                     inq[v]=1;
 61                 }
 62             }
 63         }
 64     }
 65     dis[a][b]=d[m];
 66 }
 67 
 68 int main()
 69 {
 70     //freopen("in.txt","r",stdin);
 71     while(~scanf("%d%d%d%d",&n,&m,&k,&t))
 72     {
 73         tot=0;
 74         memset(head,-1,sizeof(head));
 75         memset(flag,0,sizeof(flag));
 76         for(int i=0;i<t;i++)
 77         {
 78             int u,v,w;
 79             scanf("%d%d%d",&u,&v,&w);
 80             AddEdge(u,v,w);
 81             AddEdge(v,u,w);
 82         }
 83 
 84         scanf("%d",&t);
 85         while(t--)
 86         {
 87             int x,a,b;
 88             scanf("%d%d%d",&x,&a,&b);
 89             for(int i=a;i<=b;i++)  flag[x][i]=1;
 90         }
 91 
 92         for(int i=1;i<=m;i++)
 93             for(int j=1;j<=n;j++)  flag[i][j]+=flag[i][j-1];  //用前缀和可以快速判断i~j天是否可用
 94 
 95         for(int i=1;i<=n;i++)
 96             for(int j=i;j<=n;j++)  spfa(1,i,j);
 97 
 98         f[0] = -k;  //注意边界条件
 99         for(int i = 1; i <= n; i ++)
100         {
101             f[i] = INF;
102             for(int j = 0; j < i; j++)
103             f[i] = min(f[i], f[j] + 1LL*dis[j+1][i]*(i-j) + k);
104         }
105         printf("%d\n",f[n]);
106     }
107     return 0;
108 }
posted @ 2017-08-04 22:20  Kayden_Cheung  阅读(147)  评论(0)  编辑  收藏  举报
//目录