BZOJ 1853: [Scoi2010]幸运数字(容斥原理)
http://www.lydsy.com/JudgeOnline/problem.php?id=1853
题意:
在中国,很多人都把6和8视为是幸运数字!lxhgww也这样认为,于是他定义自己的“幸运号码”是十进制表示中只包含数字6和8的那些号码,比如68,666,888都是“幸运号码”!但是这种“幸运号码”总是太少了,比如在[1,100]的区间内就只有6个(6,8,66,68,86,88),于是他又定义了一种“近似幸运号码”。lxhgww规定,凡是“幸运号码”的倍数都是“近似幸运号码”,当然,任何的“幸运号码”也都是“近似幸运号码”,比如12,16,666都是“近似幸运号码”。 现在lxhgww想知道在一段闭区间[a, b]内,“近似幸运号码”的个数。
思路:
首先要明白一点的是,在N范围内找a或b的倍数的个数为: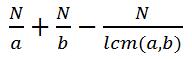
那么推广到这题的话也是差不多的,也就是容斥原理的运用。
首先可以先找出所有带6、8的数,可以优化一下删去有倍数关系的数,然后就是从中找lcm,也就是容斥原理的奇加偶减。在寻找的过程中,优先找值大的,这样一来剪枝会剪得更多一些。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<sstream> 6 #include<vector> 7 #include<stack> 8 #include<queue> 9 #include<cmath> 10 #include<map> 11 #include<set> 12 using namespace std; 13 typedef long long ll; 14 typedef pair<int,int> pll; 15 const int INF = 0x3f3f3f3f; 16 const int maxn = 1e5 + 5; 17 18 int n; 19 ll l, r; 20 ll cnt; 21 ll ans; 22 ll a[maxn]; 23 ll b[maxn]; 24 int vis[maxn]; 25 26 void init(ll x) 27 { 28 if(x>r) return; 29 if(x!=0) a[cnt++]=x; 30 init(x*10+6); 31 init(x*10+8); 32 } 33 34 ll gcd(ll a, ll b) 35 { 36 return b==0?a:gcd(b,a%b); 37 } 38 39 void dfs(int cur, int cnt, ll val) 40 { 41 if(cur>=n) 42 { 43 if(!cnt) return; 44 if(cnt&1) ans+=(r/val-(l-1)/val); 45 else ans-=(r/val-(l-1)/val); 46 return; 47 } 48 dfs(cur+1,cnt,val); 49 ll tmp=val/(gcd(a[cur],val)); 50 if((double)tmp*a[cur]<=r) 51 { 52 dfs(cur+1,cnt+1,tmp*a[cur]); 53 } 54 } 55 56 int main() 57 { 58 //freopen("in.txt","r",stdin); 59 while(~scanf("%lld%lld",&l,&r)) 60 { 61 cnt=0; 62 init(0); 63 64 n=0; 65 sort(a,a+cnt); 66 memset(vis,0,sizeof(vis)); 67 for(int i=0;i<cnt;i++) 68 { 69 if(!vis[i]) 70 { 71 b[n++]=a[i]; 72 for(int j=i+1;j<cnt;j++) 73 { 74 if(a[j]%a[i]==0) 75 vis[j]=1; 76 } 77 } 78 } 79 for(int i=0;i<n;i++) 80 a[i]=b[n-i-1]; 81 82 ans=0; 83 dfs(0,0,1); 84 printf("%lld\n",ans); 85 } 86 return 0; 87 }

