对01背包的分析与理解(图文)
首先谢谢Christal_R的文章(点击转到链接)让我学会01背包
本文较长,但是长也意味着比较详细,希望您可以耐心读完。
题目:
现在有一个背包(容器),它的体积(容量)为V,现在有N种物品(每个物品只有一个),每个物品的价值W[i]和占用空间C[i]都会由输入给出,现在问这个背包最多能携带总价值多少的物品?
一.动态规划与递推解决01背包
初步分析:
0. 浅谈问题的分解
在处理到第i个物品时,可以假设一共只有i个物品,如果前面i-1个物品的总的最大价值已经定下来了,那么第i个物品选不选将决定这1~i个物品能带来的总的最大价值
刚刚是自顶向下,接下来反过来自底向上,第1个物品选不选可以轻松地用初始化解决,接下来处理第i个物品时,假设只有2个物品就好,那他处理完后前2个物品能带来的最大总价值就确定了,这样一直推下去,就可以推出前n个物品处理完后能带来的最大总价值
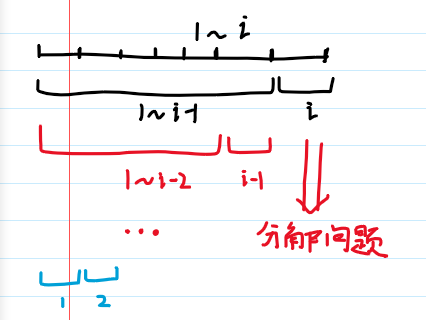
1.分层考虑解决"每个物品最多只能装一次"
每个物品只能装一次,那么就应该想到常用的一种方法,就是用数组的纵轴来解决,对于n个物品,为它赋予i=1~n的编号,那么数组的纵轴就有n层,每层只考虑装不装这个物品,那么分层考虑就可以解决最多装一个的问题了
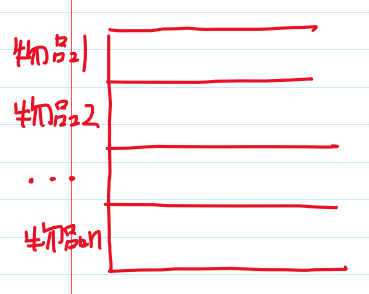
2.对0,1的理解
对于每个背包,都只有0和1的情况,也就是拿或者不拿两种情况
如果拿:那么空间就会减一点,比如说现在在考虑第i个物品拿不拿,如果说当前剩余空间为j,那么拿了之后空间就变为j-c[i],但是总价值却会增加一点,也就是增加w[i]
如果不拿:那么空间不会变,还是j,但是总价值也不会变化

3.限制条件
所以对于这题来说有一个限制条件,就是空间不超出,然后目标就是在空间不超出的情况塞入物品使总价值最大,在前面,我们已经讲了数组的纵轴用来表示当前处理到第几个物品,那么只靠这个是不够的,而且这个数组的意义还没有讲
这题就是限制条件(空间)与价值的平衡,你往背包中塞东西,价值多了,可是空间少了,这空间本来可能遇到性价比更高的物品但也可能没遇到
4.具体的建立数组解决问题
有了前面的限制情况和0,1的分析就可以建立数组了
对于这个数组,结合题目要求来说,数组的意义肯定是当前的总价值,也就是第i个物品的总价值,那么题目还有一个限制条件,只靠一个n层的一维数组是不够的,还需要二维数组的横轴来分析当前的剩余容量
所以我们有了一个数组可以来解决问题了,这个数组就叫f好了,然后它是一个二维数组,它的纵轴有i层,我希望它从i=1~n,不想从下标0开始是为了美观,然后这个二维数组的横轴代表着当前剩余的空间,就用j来表示,j=0~V,0就是没有空间的意思,V前面说了,是这个背包的总容量
我们把这个二维数组建立在int main()的上面,所以它一开始全部都是0,省去了接下来赋初值为0的功夫
有了数组f[i][j],然后对于每个f[i][j],它表示的是已经处理到第i个物品了,当剩余空间还有j时,能带有的最大价值,也就是说f[i][j]存储的是总价值
说是总价值,可是涉及到放物品还是不放物品的问题,所以再细致点就是:当前剩余空间为j,用这j空间取分析第i个物品装不装如,处理执行完行为后,f[i][j]就表示了当前能装入的最大价值

5.推导递推方程
PS:谈一下对于动态规划递推的理解:处理到第i层时,假设前i-1层的数据都知道而且可以根据1~i-1层的数据推出i,那么就成功了一半了,因为第i层如此,那么第i-1层也可以根据1~i-2层推出,接下来只需要定义好数组的初始条件和注意边缘问题以及一些细节就可以了
对于第i个物品,假设前i-1个物品都已经处理完
如果第i个物品不能放入:这种情况就是背包已经满了,也就是当前剩余空间j小于第i个物品的占用空间C[i],
这种情况下,空间没有变化,价值也没有变化,对于空间没有变化,即第i个物品的空间和第i-1个物品的空间j相同,对于价值没有变化,也就是数组f的值相同,然后开始利用前面的数据,也就是f[i][j]]=f[i-1][j]
如果第i个物品不想放入,那么和不能放入其实是一样的,动机不同但结果相同,f[i][j]]=f[i-1][j]
如果第i个物品放入了,那么f[i][j]=f[i-1][j-c[[i]]+w[i],下面解释一下这个公式,第i个物品的占用空间为c[i],价值为w[i],f[i-1][j-c[[i]]+w[i]表示前i-1个物品在给它们j-c[[i]空间时能带来的最大价值
再回到第i个物品的角度,此时有j个空间,如果已经确定要放入,为了使空间充分利用,肯定是这j个空间只分c[i](刚好够塞下第i个物品),剩下的j-c[[i]全部给前面i-1个物品自由发挥,反正前面f[i-1][j-c[[i]]已经知道了,然后前面i-1个物品用j-c[i]的空间能带来最大的利益f[i-1][j-c[[i]],第i个物品用c[i]的空间带来利益w[i],所以如果第i个物品放入后,总利益是f[i][j]=f[i-1][j-c[[i]]+w[i]
但是,长远来说,有一些偏极端情况,放入这个物品,也许它价值w[i]很高,但是它占用空间c[i]也大,它的性价比可能很低,所以这时候就需要max函数了
当还有空间时:F[i,j] = max[F[i−1,j],F[i−1,j−C[i]] + W[i]
当空间不够时:F[i,j] = F[i−1,j]
下面一个个解释:
当还有空间时:这时有两种方法,放还是不放,如果放,那么利益由两段组成1~i-1是一段,i是另一段;如果不妨,那么利益和上一层剩j空间时相同,这两个东西大小需要比较,因为如果放入,虽然加上了w[i],利益,可是冲击了前i-1个物品的利益,如果不放,那么没有收获到第i个物品的利益,但是把原来属于1~i的空间j,分给了1~i-1个物品,说不定前1~i-1的每个物品都空间小,价值高,性价比高呢?
当空间不够时,它也只能F[i,j] = F[i−1,j]了,没有选择的余地

#include<bits/stdc++.h>//万能头文件 #define ll long long using namespace std; const ll maxn=100; ll n,v,f[maxn][maxn]; ll c[maxn];//每个物品占用空间 ll w[maxn];//每个物品的价值 int main() { cin>>n>>v; for(ll i=1;i<=n;i++) scanf("%lld",&c[i]); for(ll i=1;i<=n;i++) scanf("%lld",&w[i]); for(ll i=1;i<=n;i++)//第i个物品 for(ll j=v;j>=0;j--)//剩余空间j { if(j >= c[i])//如果装得下 f[i][j]=max( f[i-1][j-c[i]]+w[i],f[i-1][j]); else//如果装不下 f[i][j]=f[i-1][j]; } cout<<f[n][v]<<endl;//输出答案 }
二.01背包的空间优化
有了前面基础版01背包的学习,现在学习这个就容易多了
1.何为空间优化,为什么要空间优化
在01背包中通过对数组的优化(用了滚动数组的方法),可以使本来N*V的空间复杂度降低到V,也就是把关于第几个物品的N去掉了(下面会解释为什么可以这么做)
至于为什么要空间优化,首先是因为递推本来就是用空间换时间,消耗的空间比较大,然后关于算法的竞赛一般都会有空间的限制要求,最后,在找工作面试时,面试官肯定会问一些优化的问题,平时养成优化的习惯面试时也有好处
2.为什么这题可以降维
通过观察可以发现对于普通版的01背包递推式,f[i][...]只和f[i-1][...]有关,那么我们可以用一种占用,一种滚动的方法来循环使用数组的空间,所以这个方法叫滚动数组,对于将来肯定用不到的数据,直接滚动覆盖即可,具体的如何滚动会放下面讲
还有就是滚动数组的缺点是牺牲了抹除了大量数据,不是每道题都可以用,但是在这,答案刚好是递推的最后一步,所以直接输出即可,递推完后不需要调用那些已经没了的数据,所以这题可以
下面先画个图理解一下滚动的大致概念
反正就是不断覆盖的过程
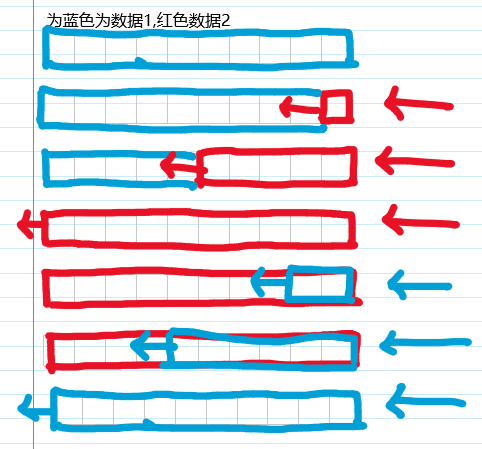
3.这题如何具体优化
下面开始具体化的分析
对于第i层,它只和第i-1层有关,但是对于剩余空间j无法优化,所以现在拿i开刀,把他砍掉,用一个长度为V(总空间)的数组来表示,然后每次相邻的两个i和i-1在上面一直滚动
所以现在建立一个数组f[V],一维数组大小为V
首先建立两个复合for循环
for(i=1~n)
for(j=v~0)
记住这里第二层循环必须是v~0而不是0~v,先记着,后面会解释,
接下来的分析建议配合下面图片学习
然后在循环的过程中,还是老样子,假设我们已经循环到i=2这层了(也就是说i=1已经循环完了),然后对于i=2这一层,我们对j循环,j从v到0
假如现在j=v,我们让f[j]=max(f[j],f[j-c[i]]+w[i])
在没有覆盖之前,所有的f数据都是属于上一层也就是第一层的,我们就当作i-1层数据已经准备好了,然后把max内的拆成两半分析,对于f[j]=f[j]就是不放的情况,那么总价值没有改变,所以对于f[j]=f[j]就是形式上的更新数据,把i-1层的f[j],给了i-1层的f[j]...对于f[j]=f[j-c[i]]+w[i],那个w[i]是肯定要加的不用讨论,然后我们观察一下,对于下标j-c[i]是不是肯定会小于j,那么如果说j从V~0也就是从最大到最小,每次赋值处理都是从前面的格子看看数据参考,并没有修改
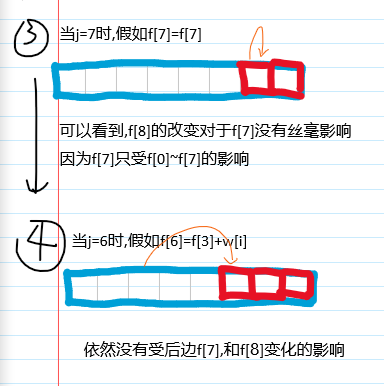
再详细点说的话就是对于f[j]=f[j-c[i]]+w[i],f[j-c[i]]是第i-1层的东西,让j=v~0是为了让f数组每次滚动覆盖时都是覆盖接下来不需要用的位置,比如说处理到第f[8]位时,假如接下来的max判定后面那种方法总价值大,然后假设c[i]=3,这时后就相当与f[8]=f[8-c[i]=5]+w[i],我们这里只是参考了f[5]的数据,并没有改变它,因为说不定计算新一轮f[6]时又要用到旧的f[5]呢,可是我们刷新了f[8]的数字后,再j--,计算f[7],再j--,计算f[6],都不会再用到f[8]这个数据,这是由于f[j-c[i]] 中的减c[i]导致的,反之,假若我们让j=0~v,就可能出现新数据被新数据覆盖的结果,我们是有"底线"的,只允许新数据覆盖旧数据
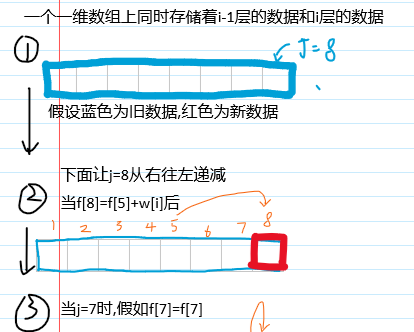
对于j,如果要处理f[j]=max(f[j],f[j-c[i]]+w[i]),就得当j>=c[i]时处理,因为如果j<c[i],那么j-c[i]为负,下标负的情况没必要考虑,如果考虑了还可能会溢出
其实对于max,还用另一个小东西代替,有没有发现,如果f[j-c[i]]+w[i]>f[j],就选f[j-c[i]]+w[i],如果f[j-c[i]]+w[i]<f[j],那选f[j]和没选一样,所以待会的空间优化版省掉了max函数,少用一种函数

#include<bits/stdc++.h>//万能头文件 #define ll long long using namespace std; const ll maxn=100; ll n,v,f[maxn]; ll c[maxn];//每个物品占用空间 ll w[maxn];//每个物品的价值 int main() { cin>>n>>v; for(ll i=1;i<=n;i++) scanf("%lld",&c[i]); for(ll i=1;i<=n;i++) scanf("%lld",&w[i]); for(ll i=1;i<=n;i++)//第i个物品 for(ll j=v;j>=1;j--)//剩余空间j { if(f[j]<=f[j-c[i]]+w[i] && j-c[i]>=0 )//二维数组变一维数组 f[j]=f[j-c[i]]+w[i];//如果值得改变并且j的空间还装得下就赋新值 } cout<<f[v]<<endl;//输出答案 }
三.初始化的细节
初始化有两种,一种情况是只要求价值最大,另外一种是要求完全刚好塞满,第一种的初始化是赋值为0,第二种的初始化是赋值为负无穷,因为没有塞满,所以数据实际上不存在,也就是让不存在的数不现实化,让与这种数相关的数据都不可用化
下面贴一些背包九讲的文字

1.4 初始化的细节问题 我们看到的求最优解的背包问题题目中,事实上有两种不太相同的问法。 有的题目要求“恰好装满背包”时的最优解,有的题目则并没有要求必须把背 包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。 3 如果是第一种问法,要求恰好装满背包,那么在初始化时除了F[0]为0,其 它F[1..V ]均设为−∞,这样就可以保证最终得到的F[V ]是一种恰好装满背包的 最优解。 如果并没有要求必须把背包装满,而是只希望价格尽量大,初始化时应该 将F[0..V ]全部设为0。 这是为什么呢?可以这样理解:初始化的F数组事实上就是在没有任何物 品可以放入背包时的合法状态。如果要求背包恰好装满,那么此时只有容量 为0的背包可以在什么也不装且价值为0的情况下被“恰好装满”,其它容量的 背包均没有合法的解,属于未定义的状态,应该被赋值为-∞了。如果背包并非 必须被装满,那么任何容量的背包都有一个合法解“什么都不装”,这个解的 价值为0,所以初始时状态的值也就全部为0了。 这个小技巧完全可以推广到其它类型的背包问题,后面也就不再对进行状 态转移之前的初始化进行讲解。


四.常数级的优化

1.5 一个常数优化 上面伪代码中的 for i = 1 to N for v = V to Ci 中第二重循环的下限可以改进。它可以被优化为 for i = 1 to N for v = V to max(V −ΣN i Wi,Ci) 这个优化之所以成立的原因请读者自己思考。(提示:使用二维的转移方程思 考较易。)

不得不说,这也太抠门了,算法效率追求到极致
五.小结
01背包很重要,是后面的基础
要学会推导状态转移方程与实现它
要学会去优化空间复杂度
PS:祝每个看到这里的人都能掌握01背包
接下来放一下代码大合集
普通版代码 #include<bits/stdc++.h>//万能头文件 #define ll long long using namespace std; const ll maxn=100; ll n,v,f[maxn][maxn]; ll c[maxn];//每个物品占用空间 ll w[maxn];//每个物品的价值 int main() { cin>>n>>v; for(ll i=1;i<=n;i++) scanf("%lld",&c[i]); for(ll i=1;i<=n;i++) scanf("%lld",&w[i]); for(ll i=1;i<=n;i++)//第i个物品 for(ll j=v;j>=0;j--)//剩余空间j { if(j >= c[i])//如果装得下 f[i][j]=max( f[i-1][j-c[i]]+w[i],f[i-1][j]); else//如果装不下 f[i][j]=f[i-1][j]; } cout<<f[n][v]<<endl;//输出答案 }
空间优化版代码 #include<bits/stdc++.h>//万能头文件 #define ll long long using namespace std; const ll maxn=100; ll n,v,f[maxn]; ll c[maxn];//每个物品占用空间 ll w[maxn];//每个物品的价值 int main() { cin>>n>>v; for(ll i=1;i<=n;i++) scanf("%lld",&c[i]); for(ll i=1;i<=n;i++) scanf("%lld",&w[i]); for(ll i=1;i<=n;i++)//第i个物品 for(ll j=v;j>=1;j--)//剩余空间j { if(f[j]<=f[j-c[i]]+w[i] && j-c[i]>=0 )//二维数组变一维数组 f[j]=f[j-c[i]]+w[i];//如果值得改变并且j的空间还装得下就赋新值 } cout<<f[v]<<endl;//输出答案 }




