一只小蜜蜂(hdoj 2044,动态规划递推)

Problem Description

有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
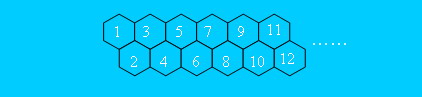
其中，蜂房的结构如下所示。

Input

输入数据的第一行是一个整数N,表示测试实例的个数，然后是N 行数据，每行包含两个整数a和b(0<a<b<50)。

Output

对于每个测试实例，请输出蜜蜂从蜂房a爬到蜂房b的可能路线数，每个实例的输出占一行。

Sample Input

2 1 2 3 6

Sample Output

1 3

//思路:
//    蜂房的旋转对称性:
//    1=>3等于2=>4//只要号码差相同结果就相同(4边形结构)
//    2=>5等于3=>6//只要号码差相同结果就相同(5边形结构)
//    然后用递推,把每个蜂房的已经存的路线+=给周围的两个格子就好了
//本题的代码只针对一组数据
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn=100;
ll f[maxn]={0};
int main()
{
    ll a,b;//a,b为蜂房号
    cin>>a>>b;
    ll n=b-a;//n为号数差

    f[1]=1;
    for(ll i=1;i<=n+1;i++)//a到b可以看成1到n+1,因为蜂房旋转对称
    {
        f[i+1]+=f[i];//把f[i]存的步数赋给f[i]旁边两个蜂房
        f[i+2]+=f[i];//建议画个图理解一下
    }
    cout<<f[n+1]<<endl;
//    比如说3到6,n=6-3=3,看成1到4,然后找出f[4]即可
}