汉诺塔解析(图解)
ps:一时学不会也没关系,过一个月再自己试试说不定就学会了
ps:图片可能加载有点慢
题目:
三个柱子,标号为1,2,3
现在告诉你柱子1上套有n个盘,问你如何把全部盘从柱子1移到柱子3
注意:盘子顺序必须时刻保持从上到下是从小到大的,一次只能移一个盘

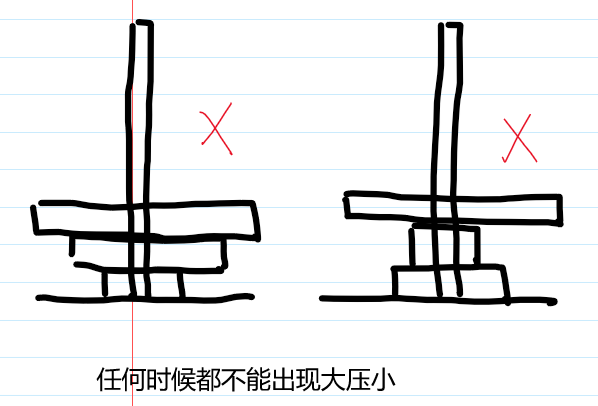
基本思路:
现在有3个柱子,分别标号为1,2,3,然后会输入一个n,代表初始的时候有几个盘子
特殊说明:输出过程的时候,把 1 -> 3 这样的结果看作从柱子1移最上面那个盘子到柱子3
比如说当三个盘子时
3 1 -> 3 1 -> 2 3 -> 2 1 -> 3 2 -> 1 2 -> 3 1 -> 3
然后开始循序渐进地解决这题
#1:

假如把一开始的n个盘子看成两部分,上面的小的和下面的大的,那么是不是只要三步就可以了
@1;把小的从1移到2
@2:把大的从1移到3
@3:把小的从2移到3
这里,1是起始柱子,2是中转站的暂时柱子,而3是终点柱子,理解这个下面的拆分就容易理解些
#2:
刚刚用的是绑定法,但是刚刚的三步,如果上面绑定的小的不止一个盘子,实际上就不能实现,因为上面的一群盘子不可能直接一次性移过去(一次只能移一个盘)
可是我们刚刚对于那一群小盘的操作是不是可以又拆分呢
也就是一开始对n-1个盘和1个盘进行了移动,那n-1个盘又可以拆分为n-2个盘和1个盘的移动
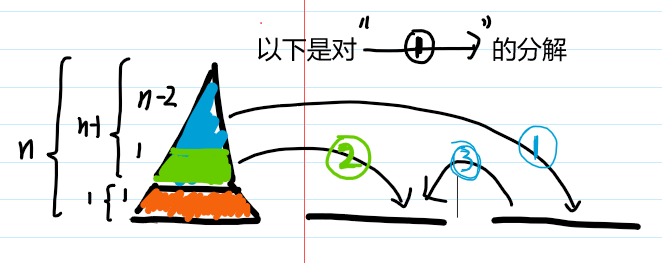
#3:具体的实现及代码

可以看到,就是把小的群移动到中转站,然后大的底盘移到终点,最后小的群移动到终点
其中,每一次小的群移动又是新的拆分,即以小的群中最下面那个做新的地盘,其他的又是更小更新的小的群
也许有人会纳闷为什么传入hanno的实参老是变化,比如说
hanno(temp,end,start,n-1);
这是因为hanno的意义就是以第一个参数为起点,以第二个参数为终点,以第三个参数为中转站,以第四个参数为当前还剩多少个盘的转移,刚刚那一步temp也许是做中转站,可是如果我们待会需要把temp的盘移到end那不仅是要把temp放第一个,end放第二个了吗,如此一来,start只能放第三个当这次的中转站
代码:
#include<bits/stdc++.h> using namespace std; int n; /* * hanno函数的意义是把当前n个盘从start移到end,用temp作为中转站 */ int hanno(int start,int end,int temp,int n) { if(n-1>=1)//如果上面的部分起码还有一个,就还要拆 hanno(start,temp,end,n-1);//把小的群移到中转站,即从start移到temp,在这过程中end是充当临时存放的地方 printf("%d -> %d\n",start,end);//把底盘从start移到end if(n-1>=1)//如果上面的部分起码还有一个,就还要拆 hanno(temp,end,start,n-1);//把小的群从中转站移到终点,即从temp移到end,也就是这时候start是充当临时存放的地方 } int main() { cin>>n; hanno(1,3,2,n); }



