【转换模型+扫描线】【UVA1398】Meteor
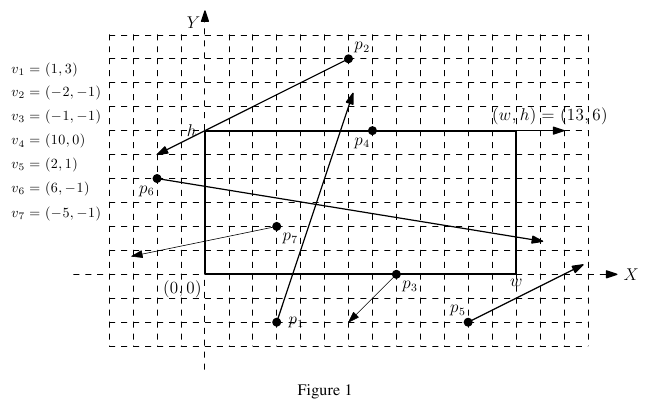
You have n meteors, each moving in uniform linear motion; the meteor mi moves along the trajectory pi + t×vi over time t , wheret is a non-negative real value, pi is the starting point of mi and vi is the velocity of mi . The point pi = (xi, yi) is represented by X -coordinate xi and Y -coordinate yi in the (X, Y) -plane, and the velocity vi = (ai, bi) is a non-zero vector with two components ai and bi in the (X, Y) -plane. For example, if pi = (1, 3) and vi = (-2, 5) , then the meteor mi will be at the position (0, 5.5) at time t = 0.5 because pi + t×vi = (1, 3) + 0.5×(-2, 5) = (0, 5.5) . The telescope has a rectangular frame with the lower-left corner (0, 0) and the upper-right corner (w, h) . Refer to Figure 1. A meteor is said to be in the telescope frame if the meteor is in the interior of the frame (not on the boundary of the frame). For exam! ple, in Figure 1, p2,p3, p4 , and p5 cannot be taken by the telescope at any time because they do not pass the interior of the frame at all. You need to compute a time at which the number of meteors in the frame of the telescope is maximized, and then output the maximum number of meteors.
Input
Your program is to read the input from standard input. The input consists of T test cases. The number of test cases T is given in the first line
of the input. Each test case starts with a line containing two integers w and h (1![]() w, h
w, h![]() 100,
000) , the width and height of the telescope frame, which are separated by single space. The second line contains an integer n , the number of input points (meteors), 1
100,
000) , the width and height of the telescope frame, which are separated by single space. The second line contains an integer n , the number of input points (meteors), 1![]() n
n![]() 100,
000 . Each of the next n lines contain four integers xi, yi, ai , and bi ; (xi, yi) is
the starting point pi and (ai, bi) is the nonzero velocity vector vi of the i -th
meteor; xi and yi are integer values between -200,000 and 200,000, and ai and bi are
integer values between -10 and 10. Note that at least one of ai and bi is not zero. These four values are separated by single spaces. We assume that all starting points pi are
distinct.
100,
000 . Each of the next n lines contain four integers xi, yi, ai , and bi ; (xi, yi) is
the starting point pi and (ai, bi) is the nonzero velocity vector vi of the i -th
meteor; xi and yi are integer values between -200,000 and 200,000, and ai and bi are
integer values between -10 and 10. Note that at least one of ai and bi is not zero. These four values are separated by single spaces. We assume that all starting points pi are
distinct.
Output
Your program is to write to standard output. Print the maximum number of meteors which can be in the telescope frame at some moment.
2 4 2 2 -1 1 1 -1 5 2 -1 -1 13 6 7 3 -2 1 3 6 9 -2 -1 8 0 -1 -1 7 6 10 0 11 -2 2 1 -2 4 6 -1 3 2 -5 -1
1 2
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <ctime>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <string>
#define oo 2000000;
#define maxn 100001
using namespace std;
struct point
{
double x;
int flag;
};
point P[maxn*10]; int tot=0;
int w,h,n;
int x,y,a,b;
int getQuJian()
{
double t1,t2;
double t3,t4;
if(a!=0)
t1=((double)(-x)/a),t2=(double)(w-x)/a;
else
{
if (0<x&&x<w) { t1=0,t2=oo;}
else
{
t1=0;t2=0;
}
}
if(b!=0)
t3=((double)(-y)/b),t4=(double)(h-y)/b;
else
{
if(0<y&&y<h){t3=0,t4=oo;}
else t3=0,t4=0;
}
if(a<0) swap(t1,t2);
if(b<0) swap(t3,t4);
if(t1>t2) return 0;
if(t3>t4) return 0;
if(t1<=t3)
{
if(t3<=t2)
{
if(t2<=t4)
{
if(t2!=t3)
{
if(t3<0&&t2>0) t3=0;
P[++tot].x=t3;P[tot].flag=0;
P[++tot].x=t2;P[tot].flag=1;
}
}
else
{
if(t3!=t4)
{
if(t3<0&&t4>0) t3=0;
P[++tot].x=t3;P[tot].flag=0;
P[++tot].x=t4;P[tot].flag=1;
}
}
}
else;
}
else
{
if(t1<=t4)
{
if(t4<=t2)
{
if(t1!=t4)
{
if(t1<0&&t4>0) t1=0;
P[++tot].x=t1;P[tot].flag=0;
P[++tot].x=t4;P[tot].flag=1;
}
}
else
{
if(t1!=t2)
{
if(t1<0&&t2>0) t1=0;
P[++tot].x=t1;P[tot].flag=0;
P[++tot].x=t2;P[tot].flag=1;
}
}
}
}
return 0;
}
int cmp(const void *i,const void *j)
{
point *ii=(point *)i,*jj=(point *)j;
if(ii->x!=jj->x)
if(ii->x>jj->x) return 1;
else return -1;
else return jj->flag-ii->flag;
}
int main()
{
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
int T,ans,now;
cin>>T;
while(T--)
{
tot=0,ans=0,now=0;
cin>>w>>h;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x>>y>>a>>b;
getQuJian();
}
qsort(P+1,tot,sizeof(P[1]),cmp);
for(int i=1;i<=tot;i++)
{
if(P[i].x>0)
{
if(P[i].flag==1) now--;
else
{
now++;
ans=max(ans,now);
}
}
else if(P[i].x==0&&P[i].flag==0)
{
now++;
ans=max(ans,now);
}
}
cout<<ans<<endl;
}
return 0;
}
刘汝佳老师的求交集写的更优美(左端点与左端点比,右端点与右端点比,并且初始区间为【0,+oo】,使得没有我那么多麻烦的判断)
void update(int x, int a, int w, double& L, double& R) {
if(a == 0) {
if(x <= 0 || x >= w) R = L-1; //无解
} else if(a > 0) {
L = max(L, -(double)x/a);
R = min(R, (double)(w-x)/a);
} else {
L = max(L, (double)(w-x)/a);
R = min(R, -(double)x/a);
}
}
【分析】
不难发现,流星的轨迹是没有直接意义的,有意义的只是每个流星在照相机视野内出现的时间段。换句话说,我们把本题抽象为这样一个问题:给出n个开区间(Li,Ri),你的任务是求出一个数t,使得包含它的区间数最多(为什么是开区间呢?请读者思考)。开区间(Li,Ri)是指所有满足Li<x <Ri的实数x的集合。
把所有区间画到平行于数轴的直线上(免得相互遮挡,看不清楚),然后想象有一条竖直线从左到右进行扫描,则问题可以转化为:求扫描线在哪个位置时与最多的开区间相交,如图1-27所示。
图 1-27
不难发现,当扫描线移动到某个区间左端点的“右边一点点”时最有希望和最多的开区间相交(想一想,为什么)。为了快速得知在这些位置时扫描线与多少条线段相交,我们再一次使用前面提到的技巧:维护信息,而不是重新计算。
我们把“扫描线碰到一个左端点”和“扫描线碰到一个右端点”看成是事件(event),则扫描线移动的过程就是从左到右处理各个事件的过程。每遇到一个“左端点事件”,计数器加1;每遇到一个“右端点事件”,计数器减1。这里的计数器保存的正是我们要维护的信息:扫描线和多少个开区间相交,如图1-28所示。
图 1-28
这样,我们可以写出这样一段伪代码。
将所有事件按照从左到右排序
while(还有未处理的事件) {
选择最左边的事件E
if(E是“左端点事件”) { cnt++; if(cnt > ans) ans= cnt; } //更新计数器和答案
else cnt--;//一定是“右端点事件”
}
这段伪代码看上去挺有道理,但实际上暗藏危险:如果不同事件的端点相同,那么哪个排在前面呢?考虑这样一种情况——输入是两个没有公共元素的开区间,且左边那个区间的右端点和右边那个区间的左端点重合。在这种情况下,两种排法的结果截然不同:如果先处理左端点事件,执行结果是2;如果先处理右端点事件,执行结果是1。这才是正确答案。
这样,我们得到了一个完整的扫描算法:先按照从左到右的顺序给事件排序,对于位置相同的事件,把右端点事件排在前面,然后执行上述伪代码的循环部分。如果你对这个冲突解决方法心存疑虑,不妨把它理解成把所有区间的右端点往左移动了一个极小(但大于0)的距离。
#include<cstdio>
#include<algorithm>
using namespace std;
//0<x+at<w
void update(int x, int a, int w, double& L, double& R) {
if(a == 0) {
if(x <= 0 || x >= w) R = L-1; //无解
} else if(a > 0) {
L = max(L, -(double)x/a);
R = min(R, (double)(w-x)/a);
} else {
L = max(L, (double)(w-x)/a);
R = min(R, -(double)x/a);
}
}
const int maxn = 100000 + 10;
struct Event {
double x;
int type;
bool operator < (const Event& a) const {
return x < a.x || (x == a.x && type > a.type); //先处理右端点
}
} events[maxn*2];
int main() {
int T;
scanf("%d", &T);
while(T--) {
int w, h, n, e = 0;
scanf("%d%d%d", &w, &h, &n);
for(int i = 0; i < n; i++) {
int x, y, a, b;
scanf("%d%d%d%d", &x, &y, &a, &b);
//0<x+at<w, 0<y+bt<h, t>=0
double L = 0, R = 1e9;
update(x, a, w, L, R);
update(y, b, h, L, R);
if(R > L) {
events[e++] = (Event){L, 0};
events[e++] = (Event){R, 1};
}
}
sort(events, events+e);
int cnt = 0, ans = 0;
for(int i = 0; i < e; i++) {
if(events[i].type == 0) ans = max(ans, ++cnt);
else cnt--;
}
printf("%d\n", ans);
}
return 0;
}
另外,本题还可以完全避免实数运算,全部采用整数:只需要把代码中的double全部改成int,然后在update函数中把所有返回值乘以lcm(1,2,…,10)=2 520即可(想一想,为什么)。
因为2520 是他们的公倍数 除出来必定是整数
void update(int x, int a, int w, int& L,int& R) {
if(a == 0){
if(x<= 0 || x >= w) R = L-1; //无解
} else if(a> 0) {
L =max(L, -x*2520/a);
R =min(R, (w-x)*2520/a);
} else {
L =max(L, (w-x)*2520/a);
R =min(R, -x*2520/a);
}
}

