语音识别算法阅读之TDNN-F

论文：

　　A time delay neural network architecture for efficient modeling of longtemporal contexts

思想：

　　对TDNN的优化改进，利用SVD将参数矩阵分解为两个更小的矩阵相乘的形势，从而减少层参数，以便利用更深的网络提取表达能力更强的特征；并且要求其中一个矩阵半正定化，使得参数矩阵随机初始化时训练不至于发散；此外，本文还在算法中引入了dropout、skip-connection、3-stages convolution等tricks，配合4-gram的语言模型，使得该算法的效果，优于TDNN、TDNN-LSTM等结构，并且解码速度更快

模型：

　　网络采用多层TDNN-F堆叠架构，并且引入了Factorized conv、across time dropout、skip-connection等tricks；此外，解码时采用了n-gram语言模型辅助提升解码效果

• TDNN-F：Factorized TDNN，顾名思义是在TDNN层基础上做的改进，将TDNN的参数矩阵M(M的行数小于列数，否则对其进行转置)通过SVD奇异值分解为两个小矩阵相乘的形式，从而有效减少层参数，以便在整体参数量相近的情况下，更好的利用网络深度带来的优势；此外，论文指出，直接采用上述形式，当网络参数随机初始化时，容易导致训练发散；于是，在Factorized TDNN更新层参数时，使得其中一个因子矩阵趋紧于α倍数的半正定化矩阵，以此来控制层参数的变化速度，使训练更稳定；

1. Factorized TDNN结构：

　　　　从TDNN角度看，Factorized TDNN相当于在两层前馈层之间引入一层瓶颈层(节点数少于隐藏层)；比如原始参数矩阵M＝700*2100，将M转化为两个因子矩阵形式有：M＝AB，其中A＝700*250，B＝250*2100，那么瓶颈层的节点数即为250；

　　　　从1d-CNN角度看，Factorized TDNN相当于引入一个3*1*700的半正定参数的卷积层，其中卷积核大小为3*1，输出通道数为700；

　　　　此外，在实践中，Factorized TDNN可以通过三种形式实现，1）3*1(半正定)->1*1; 2) 2*1(半正定)->2*1；3）2*1(半正定)->2*1(半正定)->2*1;并且提到，3卷积形式因为多出一个卷积层，时域信息会更宽；

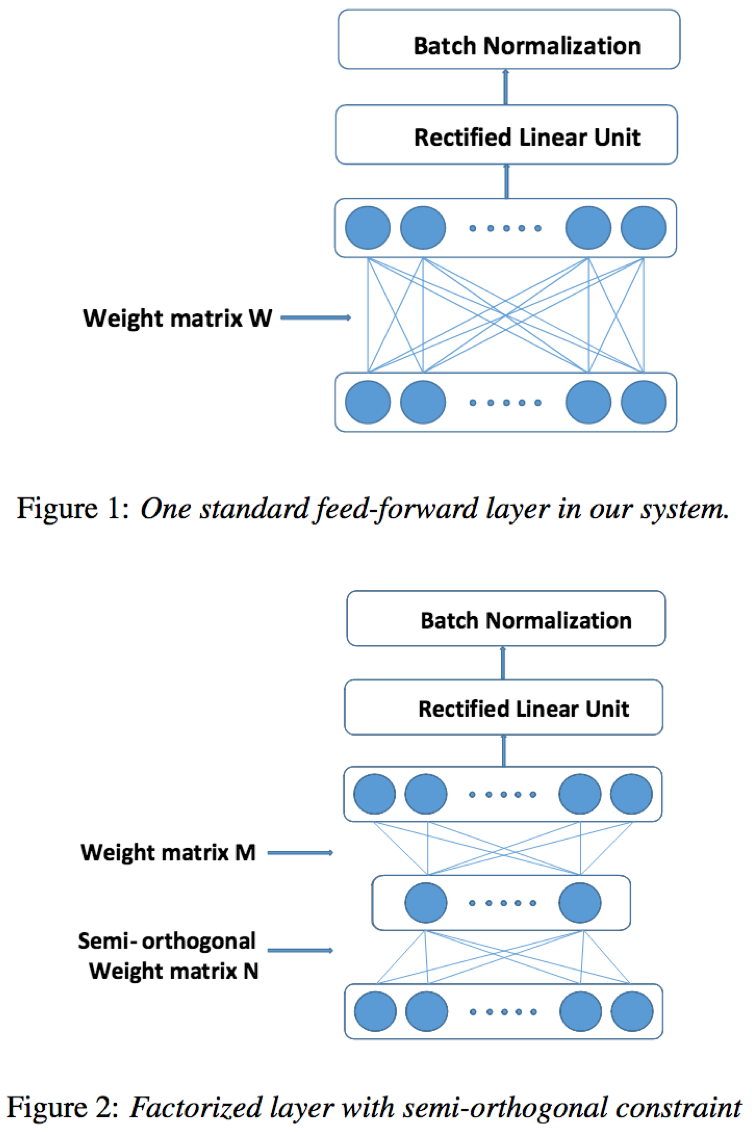
1. Factorized TDNN参数矩阵更新

　　　　假设参数矩阵M(rows>cols),定义P＝MM^T,当P＝I时，M为半正定化矩阵；令Q＝P－I，则可以通过最小化f=tr(QQ^T)来使得M趋近于I；那么目标f相对于M、P、Q的偏导数分别为：∂f/∂Q= 2Q,∂f/∂P= 2Q, and∂f/∂M= 4QM；当优化算法为SGD时，设学习率为ν= 1/8，那么可得参数矩阵M的更新公式为：

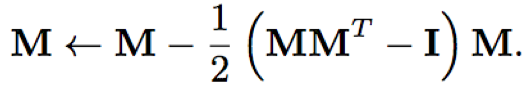
　　　　ν= 1/8使得目标函数趋近于二次收敛；tr()是对矩阵的奇异值求和计算，但是，当M离标准正交很远时，上述更新公式容易发散；但是采用Glorot-style 初始化时，即参数初始值的标准差为M列数平方根的倒数时，不容易发散

　　　　论文中提到，作者希望能够控制矩阵M的参数变化速度，使得训练更加稳定；于是，在更新参数时引入倍乘因子α，使得M趋近于α倍的半正定矩阵；此外，每层还引入l2归一化进一步使训练更稳定；变化后的参数更新公式为

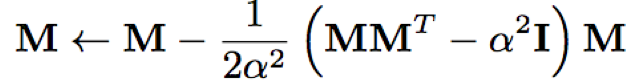
　　　　其中，α计算过程如下：

 　　　　在kaldi的具体实现中(kaldi/src/nnet3/nnet-utils.cc:ConstrainOrthonormalInternal()),为避免当M的奇异值之间差异较大导致的发散，通过减半学习率来减小发散风险；具体分析过程为：tr(P)为矩阵P奇异值(均为正)的和；tr(PP.T)为矩阵P奇异值的平房和；则奇异值mean=tr(P)/dim；且有tr(PP^T)>=dim*(tr(P)/dim)^2,即dim*tr(PP^T)>=tr(P)²；则有ratio=tr(PP^T)*dim/tr(P)²>=1,当ratio==1时，表明P的奇异值均相等，ratio>1时，ratio越大表明奇异值差异性越大，越容易造成发散；所以，当ratio>1.02时,调整学习率ν=ν*0.5来降低发散风险

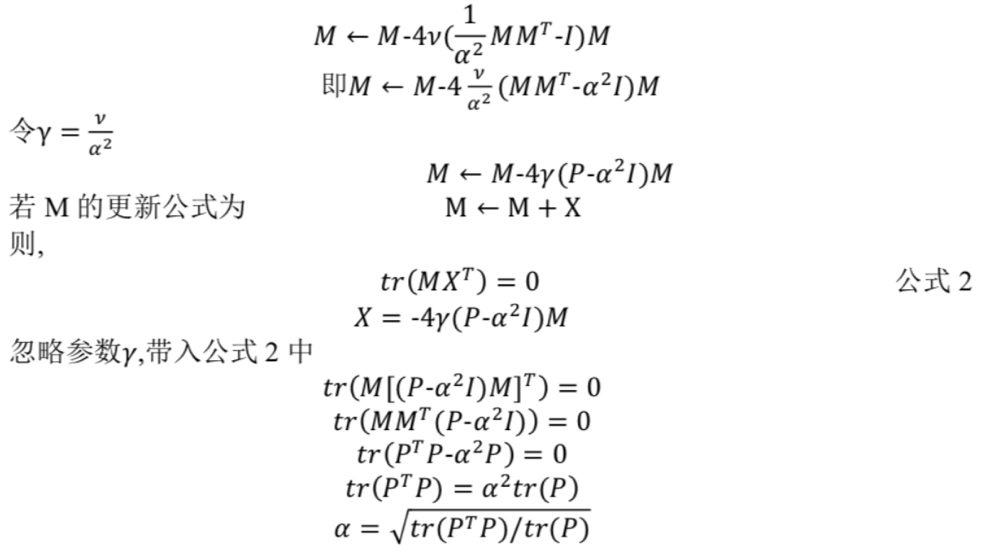
• dropout:论文采用了across time dropout，即对于一个序列，其各帧中同一维度采用相同的dropout；随机因子服从[1-2α,1+2α]的均匀分布；此外，在训练前半段，α先从0->0.5，后半段时从0.5->0;实验证明，dropout能够带来0.2％~0.3%的绝对提升
• skip-connection:跳跃连接的引入能够保证信息向深层的流入，有助于缓解梯度消失问题；实验证明，skip-connection也能带来0.2％~0.3%的绝对提升
• Factorizing the final layer：作者发现，当数据集较小时，对中间隐层进行奇异值分解对效果几乎无提升，但是对最后一层隐层进行奇异值分解时，仍然有提升

训练：

• 数据集：300小时Switchboard data；Fisher+Switchboard data combined together (2000 hours)；Swahili and Tagalogdata from the MATERIAL program (80 hours each)；3-fold 语速增强(0.9x/1.0x/1.1x)
• 测试集：HUB5’00 evaluation set
• 语言模型：Switchboard and Fisher+Switchboard：4-gram；MATERIAL setup：3-gram backoff LM+RNN LM rescore
• baseline:TDNN、TDNN-LSTM、BLSTMs
• tricks：l2归一化、α倍数的半正定约束、3-stages卷积层、dropout和skip-connection

实验：

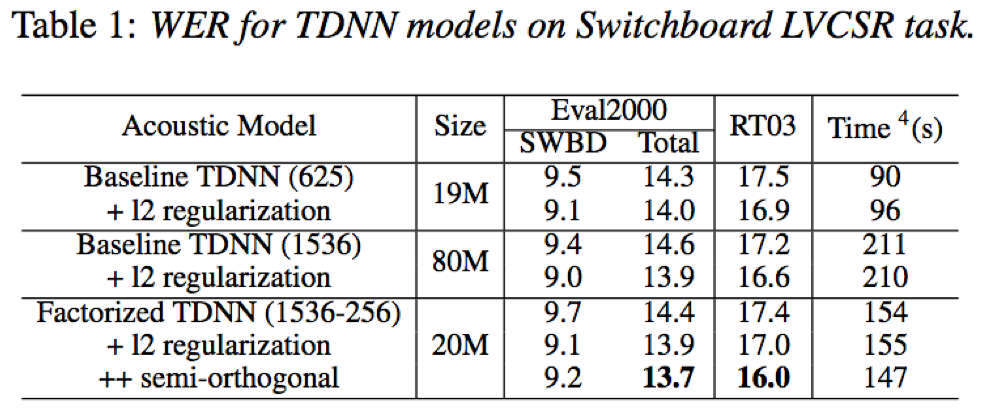
• 在大规模语音识别任务上，Factorized TDNN＋l2归一化＋半正定约束策略，相比于TDNN结构，参数量仅为1/4的条件下，依然取得更好的识别效果；此外，因为参数量更少，训练和解码速度也更快

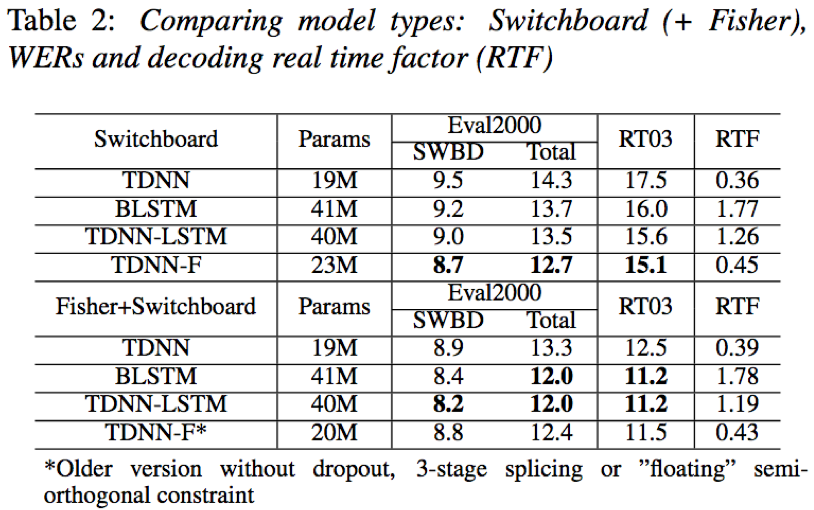
• 在300小时Switchboard数据上，TDNN-F结构相比于TDNN、BLSTM、TDNN-LSTM无论在识别效果还是解码实时因子方面，均具有一定的优势；在2000小时Fisher+Switchboard数据上，为保证解码速度，在省去3-stage splicing, dropout 和 ”floating”semi-orthogonal constraint条件下，依然能够取得可比最优的识别效果和解码性能

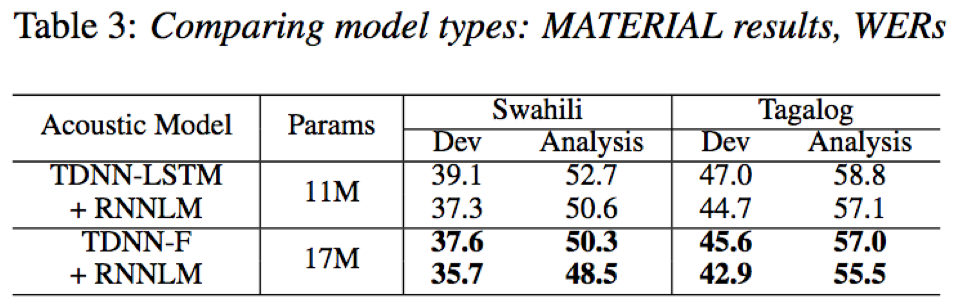
• 在MATERIAL上，TDNN-F＋RNNLM相比于TDNN-LSTM+RNNLM，在参数量相近条件下，也取得了更好的识别效果

结论：

　　本文在TDNN基础上，提出了一种因式分解的TDNN结构TDNN-F；该结构通过SVD将矩阵参数进行奇异值分解，转换成两个更小矩阵相乘的形式，并且其中一个矩阵趋紧于半正定化，一方面减少层参数，利用更深的网络结构提升效果，另一方面矩阵参数半正定化更新的策略也能保证训练的稳定性；此外，论文还结合3-stage convolution、l2归一化、dropout、skip-connection等tricks，配合语言模型，取得了比TDNN、BLSTM、TDNN-LSTM等结构更好的识别结果和更快的解码速度

实战：https://github.com/cvqluu/Factorized-TDNN

• 实现语言：pytorch
• 网络结构：

1. 1*TDNN+8*F-TDNN+1*Dense-ReLU+statspooling+2*Dense-ReLU+softmax;
2. skip-connection:

　　　　F-TDNN-4:F-TDNN-2+F-TDNN-3;

　　　　F-TDNN-6:F-TDNN-1+F-TDNN-3+F-TDNN-5

　　　　F-TDNN-8:F-TDNN-3+F-TDNN-5+F-TDNN-7

• TDNN-F结构：2*1(半正定)->2*1(半正定)->2*1

 

• 半正定卷积参数更新＋防止训练发散策略：

Reference：

[1] https://www.jianshu.com/p/ddef79012db5

[2] kaldi/src/nnet3/nnet-utils.cc

[3] https://github.com/cvqluu/Factorized-TDNN

[3] http://www.danielpovey.com/files/2018_interspeech_tdnnf.pdf(本文)