torch&numpy常用函数总结
np.dot() -向量内积
np.matmul() & @运算符-矩阵乘法
np.multiply() & *运算符-针对标量的运算(各个维度均可)
& np.square()-等价于np.multiply(a ,a)
np.c_()
a = np.array([[1,2],[3,4]])
b = np.array([5,6])
c = np.c_[a , b]
[[1,2,5],
[3,4,6]]
a = np.array([1,2,3])
b = np.array([5,6,7])
c = np.c_[a , b]
[[1,5] , [2,6] , [3,7]]
- np.c 中的c 是 column(列)的缩写,将两个列表组合(将两个列表的第一个元素组合成一个列表,举例将x,y列表拼成坐标),要求行数相等
- 通常使用np.meshgrid()得到x,y坐标之后,对x,y进行展平,然后就可以使用该函数进行拼接成一个坐标形式了
np.mean()
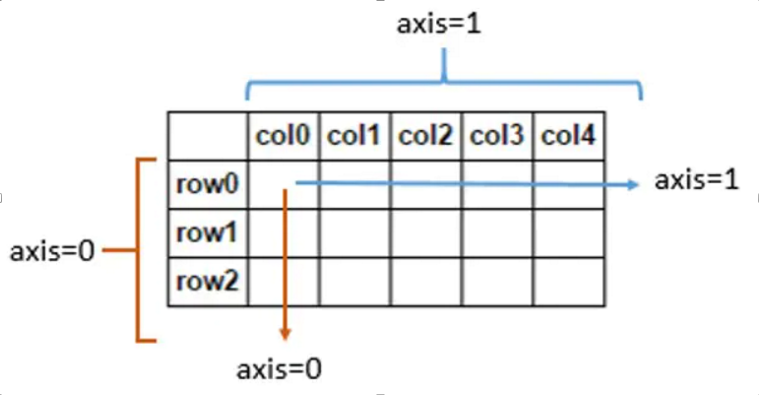
np.mean(X , axis = 0)
- axis 不设置值,对 m*n 个数求均值,返回一个实数
- axis = 0:压缩行,对各列求均值,返回 (n,)向量
- axis =1 :压缩列,对各行求均值,返回(m,)向量,二维中(axis=-1与axis=1等价)
np.std() & np.var()
np.std(X, axis=0)
np.var(X, axis=0) # 求方差
- axis 不设置值,对 m*n 个数求标准差,返回一个实数
- axis = 0:压缩行,对各列求标准差,返回 1* n 矩阵
- axis =1 :压缩列,对各行求标准差,返回 m *1 矩阵,二维中(axis=-1与axis=1等价)
np.exp()
input_array = np.array([1,2,3])
exp_array = np.exp(input_array)
- 计算e的1、2、3次方
np.log()
b = np.log(a)
b = np.log2(a)
def log(base , x):
return np.log(X)/np.log(base)
- 计算a的对数,以e为底
- 计算a以2为底的对数
- 计算以base为底,x的对数
np.zeros()
f_wb = np.zeros(5)
- 初始化数组
math.ceil()
math.ceil(19.3)
- 返回大于等于参数x的最小整数,即对浮点数向上取整.
语法糖
X_train = np.array([0., 1, 2, 3, 4, 5], dtype=np.float32).reshape(-1,1)
Y_train = np.array([0, 0, 0, 1, 1, 1], dtype=np.float32).reshape(-1,1)
pos = Y_train == 1 #[f , f , f , t , t , t].reshape(-1 , 1)
neg = Y_train == 0
X_train[pos] # [3 , 4, 5]
- 学习这一种语法糖
- 类似的,比如
centroids(ndarray(K,n) , K < m)中存放了K个簇质心,idx(ndarray(m))存放数据集中的每一个点属于哪一个簇,则将数据集中的每一个点替换为其所属簇质心的代码:X_recovered = centroids[idx , :]
>>> y = np.array([1 , 1 , 1 , 0 , 0 , 1])
>>> print(y[y == 1])
[1 , 1, 1 , 1]
- 通过这种方式,就不必使用循环的方式了
np.tile()
a = np.array([
[1,2,3] ,
[5,4,3] ,
[7,8,9]])
- x轴扩大一倍(不变),y轴扩大两倍
np.tile(a,(1,2))

- x轴扩大二倍,y轴扩大一倍(不变)
np.tile(a,(2,1))

二值化语法
yhat = (pred >= 0.5).astype(int) # 将 bool 转换成 int
numpy的矩阵运算
a = np.array([
[1 , 2 , 3],
[2 , 3 , 4]
])
b = np.array([[10 , 10 , 10]])
c = np.array([10 , 10 , 10])
d = np.array([[100] , [100]])
print(f"a.shape : {a.shape}")
print(f"b.shape : {b.shape}")
print(f"c.shape : {c.shape}")
print(f"d.shape : {d.shape}")
print("-------------------------")
print(f"a + b = {a + b}")
print(f"a + c = {a + c}")
print(f"a + d = {a + d}")
a.shape : (2, 3)
b.shape : (1, 3)
c.shape : (3,)
d.shape : (2, 1)
-------------------------
a + b = [[11 12 13]
[12 13 14]]
a + c = [[11 12 13]
[12 13 14]]
a + d = [[101 102 103]
[102 103 104]]
np.argmax() & np.argmin()
a = [3 , 45 , 1]
b = np.argmax(a) # b = 1
c = np.argmin(a) # c = 2
- 获取array的某一个维度中数值最大的那个元素的索引
np.linspace()
>>> np.linspace(2.0, 3.0, num=5)
array([ 2. , 2.25, 2.5 , 2.75, 3. ])
>>> np.linspace(2.0, 3.0, num=5, endpoint=False)
array([ 2. , 2.2, 2.4, 2.6, 2.8])
>>> np.linspace(2.0, 3.0, num=5, retstep=True)
(array([ 2. , 2.25, 2.5 , 2.75, 3. ]), 0.25)
- 生成等差数列
np.random.random_sample()
- np.random.random_sample() = np.random.sample()
>>> np.random.random_sample()
0.47108547995356098
>>> type(np.random.random_sample())
<type 'float'>
>>> np.random.random_sample((5,))
array([ 0.30220482, 0.86820401, 0.1654503 , 0.11659149, 0.54323428])
- 生成指定规模的0~1范围内的随机数
- 一维数组:(m , )
- 二维数组:(m , n)
np.random.permutation()
randidx = np.random.permutation(X.shape[0])
rand_X = X[randidx]
- 生成0~m的排列数
- 主要功能是用来产生一个随机序列作为索引,再使用这个序列从原来的数据集中按照新的随机顺序产生随机数据集
np.linalg.norm(x, ord=None, axis=None, keepdims=False)
- 计算矩阵或者向量的各种范式
- ord:
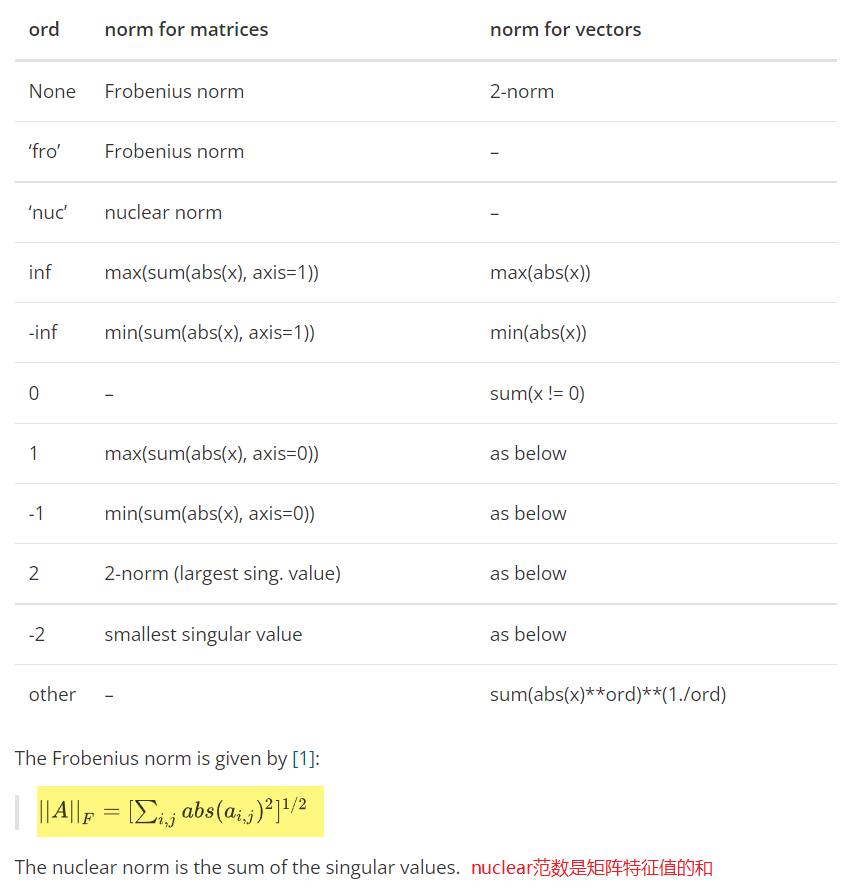
- keepdims:指输出是否应该保持矩阵形式
np.transpose()
>>> two=np.arange(16).reshape(4,4)
>>> two
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
>>> two.transpose()
array([[ 0, 4, 8, 12],
[ 1, 5, 9, 13],
[ 2, 6, 10, 14],
[ 3, 7, 11, 15]])
>>> two.transpose(1,0)
array([[ 0, 4, 8, 12],
[ 1, 5, 9, 13],
[ 2, 6, 10, 14],
[ 3, 7, 11, 15]])
- 该函数对于一维矩阵不起作用,对于二维矩阵相当于转置操作
np.all() & np.any()
- np.all(np.array) 对矩阵所有元素做与操作,所有为True则返回True
- np.any(np.array) 对矩阵所有元素做或运算,存在True则返回True
- 例如,我要求某矩阵A前n行是否全为零,则可通过以下方式:
if np.all(A[:n, :] == 0):
print("A矩阵前n行所有元素均为零")
# A[:n, :] == 0, A中的元素为零时则变为True, 不为零时则变为False。
# 只有当所有元素都为零才会返回所有元素都为True的矩阵
np.argsort()
- 函数功能:将a中的元素从小到大排列,提取其在排列前对应的index(索引)输出。
- 用途:需要对三个数组按照第一个数组元素大小顺序进行统一-排序,则使用该函数取得第一个数组a排序后的idx,然后直接b[idx]即可完成b的协同排序
x=np.array([1,4,3,-1,6,9])
y=np.argsort(x)
print('一维数组的排序结果:{}'.format(y))
>>> 一维数组的排序结果:[3 0 2 1 4 5]
np.masked_array()
>>> import numpy as np
>>> import numpy.ma as ma
>>> x = np.array([1, 2, 3, -1, 5])
如果我们希望-1被标记为无效
则可以:
>>> mask = (x == -1)
>>> mx = ma.masked_array(x, mask=mask)
当计算平均值时,不会考虑无效
>>> mx.mean()
2.75
>>> mx
[1 ,2 , 3 , - , 5]
- 该函数用以掩膜,被掩盖的元素不会参与后续计算
np.eye() & np.identity()
- numpy.eye(N,M=None,k=0,dtype=<class 'float'>,order='C)
- 返回的是一个二维2的数组(N,M),对角线的地方为1,其余的地方为0.
- N指定矩阵的行数,M指定列数,默认与N相同
- k:对角线的下标,默认为0表示的是主对角线,负数表示的是低对角,正数表示的是高对角。
- dtype:数据的类型,可选项,返回的数据的数据类型
- order:{‘C’,‘F'},可选项,也就是输出的数组的形式是按照C语言的行优先’C',还是按照Fortran形式的列优先‘F'存储在内存中
import numpy as np
a=np.eye(3)
print(a)
a=np.eye(4,k=1)
print(a)
a=np.eye(4,k=-1)
print(a)
a=np.eye(4,k=-3)
print(a)
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
[[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]
[0. 0. 0. 0.]]
[[0. 0. 0. 0.]
[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]]
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]
[1. 0. 0. 0.]]
np.identity(n,dtype=None)
- 只能返回主对角线上为1的方阵
填充数组
torch.zeros((2, 3, 4))
torch.ones((2, 3, 4))
torch.randn(3, 4) # 每个元素都从均值为0、标准差为1的标准⾼斯分布(正态分布)中随机采样
张量连结
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
广播机制
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a + b
- 将两个矩阵⼴播为⼀个更⼤的3 × 2矩阵,如下所⽰:矩阵a将通过复制列变成一个3*2矩阵,矩阵b将通过复制⾏变成一个3*2矩阵,然后再按元素相加
- 更一般的说,对于(m,n)的矩阵与(1,n)或者(m,1)的“向量”进行运算时,都会触发“向量”的广播机制
tensor([[0, 1],
[1, 2],
[2, 3]])
张量、ndarray、python标量互转
A = X.numpy()
B = torch.tensor(A)
a = torch.tensor([3.5])
a.item(), float(a), int(a)
二维张量转置
A.T
深拷贝
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存,将A的⼀个副本分配给B
axis的其他知识
- 降维计算时保持维度
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
sum_A = A.sum(axis=1, keepdims=True) # 保持维度
sum_A
>>>
tensor([[ 6.],
[22.],
[38.],
[54.],
[70.]])
- 特殊的累积计算:
cumsum
A.cumsum(axis=0)
>>>
tensor([[ 0., 1., 2., 3.],
[ 4., 6., 8., 10.],
[12., 15., 18., 21.],
[24., 28., 32., 36.],
[40., 45., 50., 55.]])
语法糖
- 利用语法选择targets对应的y_hat,以便于计算loss
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
print(y_hat[[0, 1], y])
print(y_hat[range(len(y_hat) - 1) , y])
>>>
tensor([0.1000, 0.5000])
tensor([0.1000, 0.6000])
- 元组/列表连结
a = (0.9 , 0.1)
b = 0.9
print(a + (b , ))
>>>
(0.9, 0.1, 0.9)
numpy.reshape的原理
- 感觉就是按照内存中的排列顺序,顺序往下取元素
X = np.array([[[1,2,3] , [4,5,6]], # 2 2 3
[[3,2,1] , [6,5,4]]
])
print(X.reshape(-1 , 6))
print(X.reshape(6 , -1))
print(X.reshape(3 , -1))
>>>
[[1 2 3 4 5 6]
[3 2 1 6 5 4]]
[[1 2]
[3 4]
[5 6]
[3 2]
[1 6]
[5 4]]
[[1 2 3 4]
[5 6 3 2]
[1 6 5 4]]
numpy.power()
- 计算幂次方
- 例三的扩充方式和例二类似,但是例三是多行数据,可以用来生成训练集某一特征的多项式
- 例四是两个大小相同的矩阵,则对应标量乘法,得到相同大小的矩阵
np.power([2,3,4] , 3)
>>> [ 8 27 64]
np.power(2, [2,3,4])
>>> [ 4 8 16]
np.power([[2] , [3]] , [1 ,2])
>>> [[2 ,4] , [3 , 9]]
np.power([2,3], [3,4])
>>> [ 8 81]
torch.meshgrid()
- torch.meshgrid函数分别传入行坐标和列坐标,生成网格行坐标矩阵和网格列坐标矩阵
- 功能:假设x是垂直方向的标识,y是水平方向的标识,通过该函数可以将其拓展成一个矩阵,矩阵中每一个像素的(x,y)由X,Y对应位置的元素表示
x = torch.tensor([1,2,3])
y = torch.tensor([4,5])
X , Y = torch.meshgrid(x , y , indexing='ij')
print(X);print(Y)
X , Y = torch.meshgrid(x , y , indexing='xy')
print(X);print(Y)
tensor([[1, 1],
[2, 2],
[3, 3]])
tensor([[4, 5],
[4, 5],
[4, 5]])
tensor([[1, 2, 3],
[1, 2, 3]])
tensor([[4, 4, 4],
[5, 5, 5]])
torch.stack() & torch.cat()
- 两个张量连接函数
- cat:连接但是不增加维度,会把每一项之间的括号消去
- stack:连接但是增加一维,保留每一项之间的括号
- dim:指具体在哪一个维度上进行张量连接
x1 = torch.tensor([0,1,2])
y1 = torch.tensor([0,11,2])
x2 = torch.tensor([10,11,12])
y2 = torch.tensor([20,21,22])
print(torch.stack((x1,y1,x2,y2)))
print(torch.stack((x1,y1,x2,y2) , dim=-1))
print(torch.cat((x1,y1,x2,y2)))
print(torch.cat((x1,y1,x2,y2) , dim=-1))
tensor([[ 0, 1, 2],
[ 0, 11, 2],
[10, 11, 12],
[20, 21, 22]])
tensor([[ 0, 0, 10, 20],
[ 1, 11, 11, 21],
[ 2, 2, 12, 22]])
tensor([ 0, 1, 2, 0, 11, 2, 10, 11, 12, 20, 21, 22])
tensor([ 0, 1, 2, 0, 11, 2, 10, 11, 12, 20, 21, 22])
torch.repeat() & torch.repeat_interleave()
- 矩阵复制,repeat是整个矩阵一起复制,而repeat_interleave是一行/一列的复制
- 应用场景:假设矩阵X是所有像素点的坐标,矩阵Y是锚框的半高宽,则想要得到每一个像素点的所有锚框的左上右下顶点坐标需要对X使用repeat_interleave(),对Y使用repeat()函数,然后相加
x = torch.tensor([[1,2],[3,4]])
print(x.repeat(2,2))
print(x.repeat_interleave(2 , dim = 0))
print(x.repeat_interleave(3 , dim = 1))
tensor([[1, 2, 1, 2],
[3, 4, 3, 4],
[1, 2, 1, 2],
[3, 4, 3, 4]])
tensor([[1, 2],
[1, 2],
[3, 4],
[3, 4]])
tensor([[1, 1, 1, 2, 2, 2],
[3, 3, 3, 4, 4, 4]])
torch.squeeze() & torch.unsqueeze()
- squeeze():压榨,减小列表的维度
- unsqueeze():在指定维度上拓展
x1 = torch.zeros((1,3,4,1))
print(x1.squeeze().shape)
print(torch.squeeze(x1 , dim=0).shape)
print(torch.squeeze(x1 , dim=1).shape) # 大小不发生改变
print(torch.unsqueeze(x1 , dim=1).shape)
print(torch.unsqueeze(x1 , dim=2).shape)
torch.Size([3, 4])
torch.Size([3, 4, 1])
torch.Size([1, 3, 4, 1])
torch.Size([1, 1, 3, 4, 1])
torch.Size([1, 3, 1, 4, 1])
在列表中插入None关键字
- 等价于增添一个维度
- 在下例中:使用None拓展维度之后,就可以实现两个列表元素一一比较大小的效果(即1,1 1,2 , 2,1 , 2,2),如果每一组是多个元素,则对应位置比较出较大值,最后形成新的max组
X = torch.arange(0 , 8 , 1)
X = X.reshape((2, 4))
print(X)
print(X[: , :2])
print(X[: , None , :2])
Y = torch.max(X[: , None , :2] , X[: , :2])
print(Y.shape)
print(Y)
tensor([[0, 1, 2, 3],
[4, 5, 6, 7]])
tensor([[0, 1],
[4, 5]])
tensor([[[0, 1]],
[[4, 5]]])
torch.Size([2, 2, 2])
tensor([[[0, 1],
[4, 5]],
[[4, 5],
[4, 5]]])
torch.max() & torch.argmax()
- argmax():会把列表平铺之后,然后得出最大元素的下标
x1 = torch.tensor([[1,2] , [3,4]])
x2 = torch.tensor([[1,2] , [0,9]])
y = torch.max(x1 , x2)
print(y.shape)
print(y)
x1 = torch.tensor([[1,2] , [3,4]])
print(torch.argmax(x1))
torch.Size([2, 2])
tensor([[1, 2],
[3, 9]])
tensor(3)
生成坐标
- 生成坐标-meshgrid
- 交换维度-permute,使用之后可能数据在内存中就不连续了,所以使用contiguous
- cv读到的图像为[h,w,c],图像通道为BGR,所以需要先将BGR转RGB,然后再通过transpose调换维度
yv, xv = torch.meshgrid([torch.arange(self.ny, device=device),
torch.arange(self.nx, device=device)])
p = p.view(bs, self.na, self.no, self.ny, self.nx).permute(0, 1, 3, 4, 2).contiguous()
img[:, :, ::-1].transpose(2, 0, 1)
torch.arange()
torch.arange(0, 6):生成顺序数字
torch.cumsum()
在不同维度上计算累计和
a = torch.arange(0, 6).view(2, 3)
b = a.cumsum(dim=0)
c = a.cumsum(dim=1)
b = tensor([[0, 1, 2],
[3, 5, 7]])
c=tensor([[ 0, 1, 3],
[ 3, 7, 12]])

