有向图的强连通分量
简介
-
连通分量:在一个有向图中,对于分量中的任意两点
u,v,必然可以从u走到v,且可以从v走到u -
强连通分量:对于一个连通分量,加上任何一些点之后,都不再是连通分量,则这个连通分量就是强连通分量
-
应用:将有向图通过缩点的方式转化成拓扑图(DAG),从而使得问题方便求解
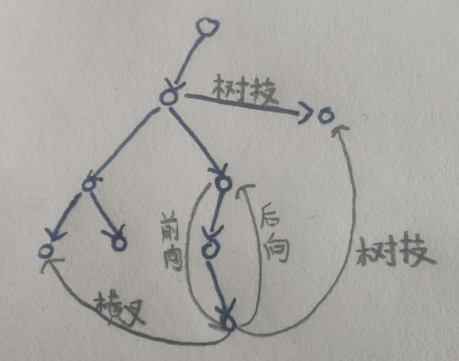
DFS搜索树中边的分类
- 树枝边:最常见的由
x指向y的边,是特殊的前向边 - 前向边:跨越一些点,指向深度较大的点的边
- 后向边:跨越一些点,指向已经遍历过的,深度较小的点的边
- 横叉边:指向树的另一已遍历分支中的点的边
什么情况会构成强连通分量(SCC)
- 存在后向边指向祖先节点
- 当前点通过横叉边指向已遍历节点,在由此节点通过后向边指向公共祖先
Tarjan算法求SCC
对于某个点定义两个时间戳:
-
dfn[u]表示遍历到u的时间戳 -
low[u]表示从u开始走,所能遍历到的最小时间戳是什么 -
则
u是其所在强连通分量的最高点,等价于dfn[u]==low[u]
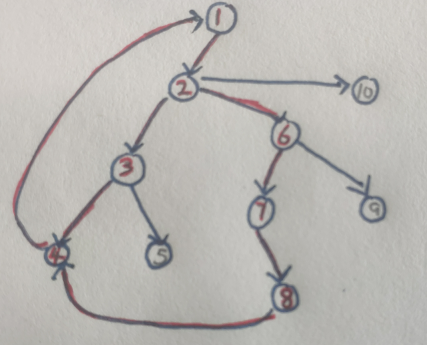
每一节点的标号即为dfn[u]的值,红色标出的节点构成了一个SCC
模板
void tarjan(int u)
{
dfn[u] = low[u] = ++ timestamp;
stk[++ top] = u , in_stk[u] = true;
for(int i = h[u]; ~i; i = ne[i])
{
int v = e[i];
if(!dfn[u])
{
tarjan(v);
low[u] = min(low[u] , low[v]);
}
else if(in_stk[v])
low[u] = min(low[u] , dfn[v]);
}
if(dfn[u] == low[u])
{
int y;
++ scc_cnt;
do{
y = stk[top--];
in_stk[y] = false;
id[y] = scc_cnt;
} while(y != u);
}
}
缩点
for(int u = 1; u <= n; u ++) //遍历所有点
for(int i = h[u]; ~i; i = ne[i]) //遍历临点
{
int v = e[i];
if(id[u] != id[v]) add(u , v); //如果不在同一SCC中则建一条边
}
SCC编号递减的顺序就是拓扑序
按照DFS的搜索顺序,当一个强连通分量的所有后继一定会先于它搜索完成,所以SCC的逆序就是拓扑序
例题-受欢迎的牛
题解
使用tarjan算法求SCC,通过缩点在建立DAG时,统计每一个SCC的出度
- 仅有一个SCC出度为0,则答案就是这个SCC中节点的个数
- 有多个SCC出度为0,则答案为0,因为这些SCC之间不能连通
代码
#include <iostream>
#include <cstring>
using namespace std;
const int N = 10010 , M = 50010;
int stack[N] , top;
bool in_stk[N];
int e[M] , ne[M] , h[N] , idx;
int id[N] , Size[N] , scc_cnt;
int dfn[N] , low[N] , timestamp;
int dout[N];
int n , m;
void tarjan(int u)
{
dfn[u] = low[u] = ++timestamp;
stack[++top] = u , in_stk[u] = true;
for(int i = h[u]; ~i; i = ne[i])
{
int v = e[i];
if(!dfn[v])
{
tarjan(v);
low[u] = min(low[u] , low[v]);
}
else if(in_stk[v])
low[u] = min(low[u] , dfn[v]);
}
if(dfn[u] == low[u])
{
int y;
++ scc_cnt;
do{
y = stack[top --];
in_stk[y] = false;
id[y] = scc_cnt;
Size[scc_cnt]++;
} while(y != u);
}
}
void add(int l , int r)
{
e[idx] = r , ne[idx] = h[l] , h[l] = idx ++;
}
int main()
{
cin >> n >> m;
memset(h , -1 , sizeof h);
while(m -- )
{
int a, b;
cin >> a >> b;
add(a , b);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i);
for(int u = 1; u <= n; u++)
for(int j = h[u]; ~j; j = ne[j])
{
int v = e[j];
if(id[v] != id[u]) dout[id[u]]++;
}
int sum = 0, cnt = 0;
for(int i = 1; i <= scc_cnt; i++)
{
if(!dout[i])
{
sum += Size[i];
cnt++;
if(cnt > 1) { sum = 0; break;}
}
}
cout << sum << endl;
return 0;
}
例题-学校网络
题解
通过求SCC后,进行缩点求出DAG之后:
- 只需要给所有入度为0的点提供软件即可
- 结论:假设入度为0点为A类点,有\(a\)个,出度为0点为B类点,有\(b\)个,则至少需要连接
max(a, b)条边
证明上述结论:
假设 \(a \leq b\) (\(a \geq b\) 的情况可以对称证明)
- \(a=1\) , 所有B类点必须建边到A类点上,且只需要建立这些边.
- 一般情况, 将任意一个B类点连接到任意一个A类点上。则\(a,b\)同时减1;按照上述过程,直到\(a=1\);即转化成了和(1)相同的情况,所以总共只需要连接b条边
代码
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110 , M = N * N;
int stk[N] , top;
bool in_stk[N];
int h[N] , e[M] , ne[M] , idx;
int dfn[N] , low[N] , timestamp;
int id[N] , scc_cnt;
int din[N] , dout[N];
int n;
void add(int l , int r)
{
e[idx] = r , ne[idx] = h[l] , h[l] = idx ++;
}
void tarjan(int u)
{
dfn[u] = low[u] = ++ timestamp;
stk[++ top] = u , in_stk[u] = true;
for(int i = h[u]; ~i; i = ne[i])
{
int v = e[i];
if(!dfn[v])
{
tarjan(v);
low[u] = min(low[u] , low[v]);
}
else if(in_stk[v])
low[u] = min(low[u] , dfn[v]);
}
if(dfn[u] == low[u])
{
int y;
++ scc_cnt;
do{
y = stk[top--];
in_stk[y] = false;
id[y] = scc_cnt;
} while(y != u);
}
}
int main()
{
cin >> n;
memset(h , -1 , sizeof h);
for(int i = 1; i <= n; i++)
{
int t;
while(cin >> t , t)
add(i , t);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i);
//缩点
for(int u = 1; u <= n; u++)
for(int i = h[u]; ~i; i = ne[i])
{
int v = e[i];
if(id[u] != id[v]) din[id[v]]++ , dout[id[u]]++;
}
int a = 0 , b = 0;
for(int i = 1; i <= scc_cnt; i++)
{
if(!din[i]) a++;
if(!dout[i])b++;
}
cout << a << endl;
if(scc_cnt == 1) cout << 0 << endl;
else cout << max(a , b) << endl;
return 0;
}
参考文献
Acwing-算法提高课-图论章节
https://www.acwing.com/activity/content/introduction/16/

