刷题笔记-DP
从集合角度分析DP -闫氏dp法
https://www.acwing.com
01背包问题

思路:
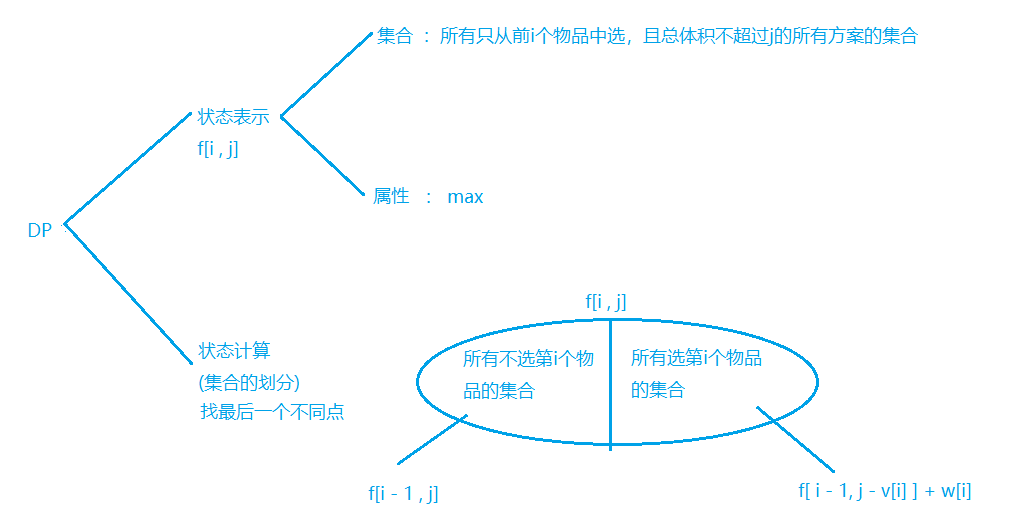
代码1:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int dp[N][N];
int a[N][2];
int n,v;
int main()
{
cin >> n >> v;
for(int i = 1; i <= n;i++)
for(int j = 0; j < 2;j++)
cin >> a[i][j];
for(int i = 1; i <= n;i++) //第几个重物
for(int j = 1;j <= v;j++){ //容量
int tmp = j - a[i][0];
if(tmp < 0)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = max(a[i][1] + dp[i-1][tmp] , dp[i-1][j] );
}
cout << dp[n][v] << endl;
return 0;
}
代码2 - 空间优化
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int dp[N];
int n,m;
int main()
{
cin >> n >> m;
for(int i = 1; i <= n;i++)
{
int v,w;
cin >> v >> w;
for(int j = m; j >= v;j--)
dp[j] = max(dp[j] , dp[j-v] + w);
}
cout << dp[m] << endl;
return 0;
}
摘花生
Hello Kitty想摘点花生送给她喜欢的米老鼠。
她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。
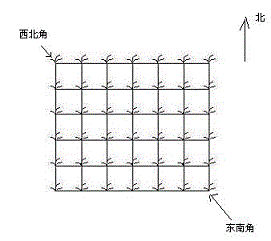
地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走,不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。
输入格式
第一行是一个整数T,代表一共有多少组数据。
接下来是T组数据。
每组数据的第一行是两个整数,分别代表花生苗的行数R和列数 C。
每组数据的接下来R行数据,从北向南依次描述每行花生苗的情况。每行数据有C个整数,按从西向东的顺序描述了该行每株花生苗上的花生数目M。
输出格式
对每组输入数据,输出一行,内容为Hello Kitty能摘到得最多的花生颗数。
数据范围
\(1≤T≤100\)
\(1≤R,C≤100\)
\(0≤M≤1000\)
思路:
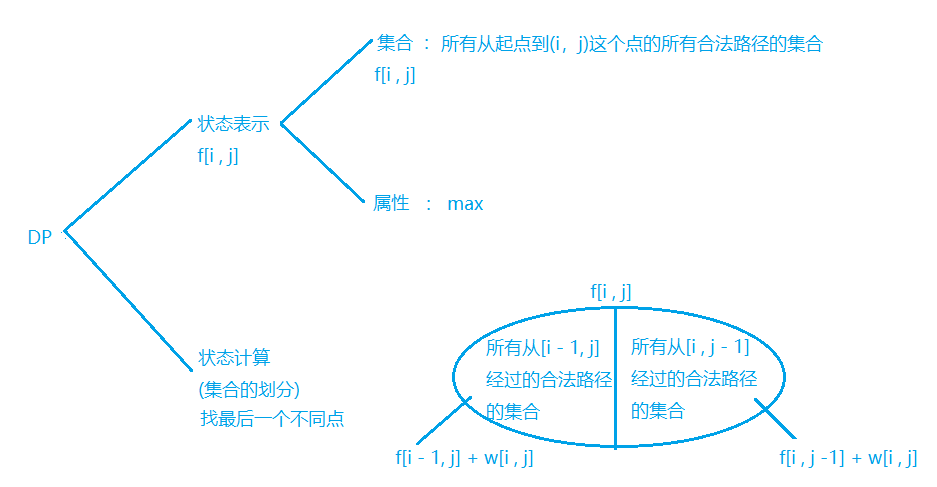
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 105;
int a[N][N],dp[N][N];
int main(void)
{
int t;
cin >> t;
while(t--)
{
int r,c;
cin >> r >> c;
for(int i = 1 ; i <= r ; i++ )
for(int j = 1 ; j <= c ; j++ )
scanf("%d",&a[i][j]);
for(int i = 1;i <= r;i++)
for(int j = 1;j <= c;j++)
dp[i][j] = max(dp[i-1][j] + a[i][j], dp[i][j-1] + a[i][j]);
cout << dp[r][c] << endl;
}
return 0;
}
最长上升子序列
给定一个长度为N的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数N。
第二行包含N个整数,表示完整序列。
输出格式
输出一个整数,表示最大长度。
数据范围
\(1≤N≤1000\)
\(10^9≤数列中的数≤10^9\)
思路:
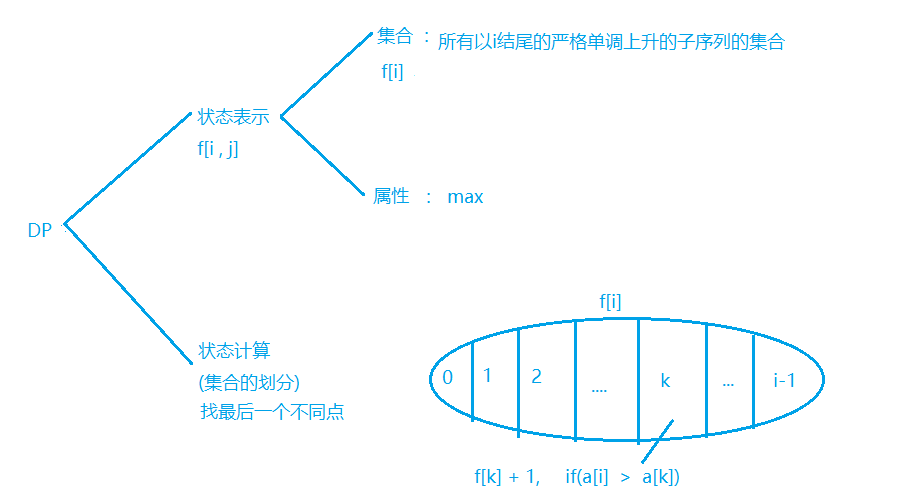
代码:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int a[N],dp[N];
int main(void)
{
int n,ans = 0;
cin >> n;
for(int i = 1;i <= n;i++)
cin >> a[i];
for(int i = 1; i <= n; i++)
{
//预处理,至少只含本身,则序列长度为1
dp[i] = 1;
for(int j = 1; j < i; j++)
if(a[i] > a[j])
dp[i] = max(dp[i], dp[j] + 1);
ans = max(ans , dp[i]);
}
cout << ans << endl;
return 0;
}
代码2 - 使用二分优化
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int a[N],dp[N];
int main(void)
{
int n;
cin >> n;
for(int i = 0;i < n;i++)
cin >> a[i];
int j = 0;dp[0] = a[0];
for(int i = 1; i < n;i++)
{
int l = 0,r = j;
while(l < r)
{
int mid = l + r >> 1;
if(a[i] <= dp[mid])
r = mid;
else
l = mid + 1;
}
//特判
if(r == j && a[i] > dp[j])
dp[++j] = a[i];
else
dp[r] = a[i];
}
cout << j+1 << endl;
return 0;
}
地宫取宝
X 国王有一个地宫宝库,是 n×m个格子的矩阵,每个格子放一件宝贝,每个宝贝贴着价值标签。
地宫的入口在左上角,出口在右下角。小明被带到地宫的入口,国王要求他只能向右或向下行走。
走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。
当小明走到出口时,如果他手中的宝贝恰好是 k件,则这些宝贝就可以送给小明。
请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这k件宝贝。
输入格式
第一行3个整数,
n,m,k
接下来n行,每行有 m个整数 用来描述宝库矩阵每个格子的宝贝价值。
输出格式
输出一个整数,表示正好取 k个宝贝的行动方案数。该数字可能很大,输出它对1000000007取模的结果。
数据范围
\(1≤n,m≤50\)
\(1≤k≤12\)
\(0≤宝贝的价值≤12\)
思路:
1.数据范围很小,这说明For循环可能多重,dp数组的维度也可能有多维。
2.这一题是 前面 摘花生和最长上升子序列两个问题的组合。
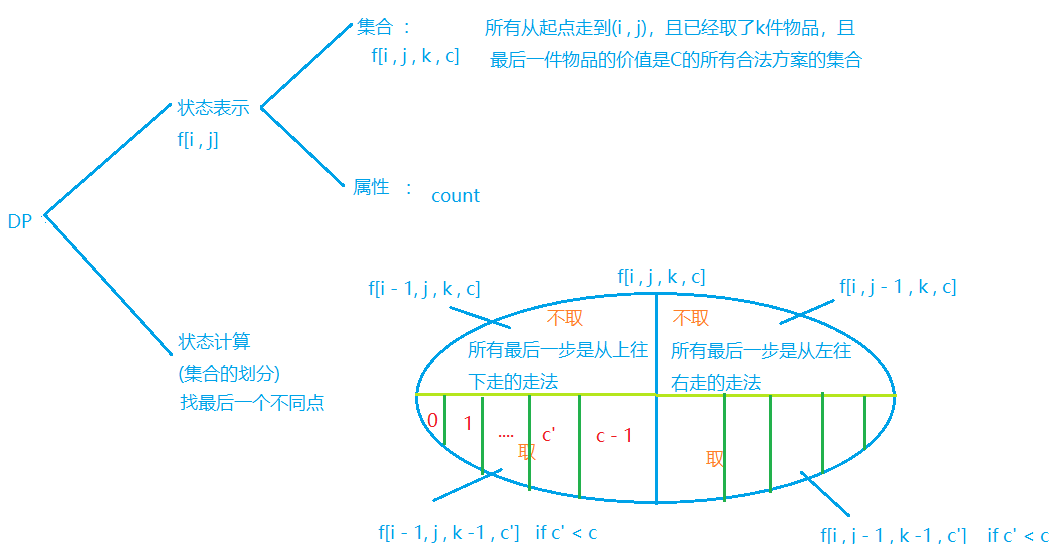
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 52, K = 14,MOD = 1000000007;
int w[N][N],f[N][N][K][K];
int n,m,k;
int main(void)
{
cin >> n >> m >> k;
for(int i = 1; i <= n;i++)
for(int j = 1; j <= m;j++)
{
cin >> w[i][j];
w[i][j]++;
}
//边界处理
//w++表示如果拿了宝贝,一定存在价值,则w = 0 可以代表没有拿宝贝
//k = 0代表一个都不拿,也算一种方案数
f[1][1][0][0] = 1;
f[1][1][1][w[1][1]] = 1;
//dp[i,j,num,c,val]表示走到坐标(i,j)拿了num个宝贝,且最大价值为val的总行动方案数
//如果不取(i,j)处的宝贝,则dp[i,j,num,val] += dp[i-1,j,num,val] + dp[i,j-1,num,val]
//如果取(i,j)处的宝贝,则dp[i,j,num,val] += dp[i-1,j,num-1,v'] + dp[i,j-1,num,val] (w[i,j] == val, v' < val)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
for(int num = 0; num <= k; num++)
for(int val = 0; val <= 13; val++) //因为不拿这个方案对应val == 0所以从0开始遍历
{
//必须两个数就要模一次,否则可能3 * 10^9,可能溢出int
f[i][j][num][val] = ( f[i][j][num][val] + f[i-1][j][num][val]) % MOD;
f[i][j][num][val] = ( f[i][j][num][val] + f[i][j-1][num][val]) % MOD;
//num > 0表示 num = 1时从没有拿到拿一个的情况
if(w[i][j] == val && num > 0)
for(int v = 0; v < val; v++)
{
f[i][j][num][val] = ( f[i][j][num][val] + f[i-1][j][num-1][v] ) % MOD;
f[i][j][num][val] = ( f[i][j][num][val] + f[i][j-1][num-1][v] ) % MOD;
}
}
int ans = 0;
for(int val = 1;val <= 13;val++)
ans = ( f[n][m][k][val] + ans) % MOD;
cout << ans << endl;
return 0;
}
代码还是比较麻烦的,尤其需要注意边界的处理
波动数列
观察这个数列:
1 3 0 2 -1 1 -2 …
这个数列中后一项总是比前一项增加2或者减少3,且每一项都为整数。
栋栋对这种数列很好奇,他想知道长度为n和为s而且后一项总是比前一项增加a或者减少b的整数数列可能有多少种呢?
输入格式
共一行,包含四个整数n,s,a,b,含义如前面所述。
输出格式
共一行,包含一个整数,表示满足条件的方案数。
由于这个数很大,请输出方案数除以100000007的余数。
数据范围
\(1≤n≤1000\)
\(-10^9<=s<=10^9\)
\(1<=a,b<=10^6\)
思路:
1.推导
- 假设符合条件的整数数列起始为x,后一项是前一项+a或-b,将这个操作统一为d_i = {a,-b};
- 则数列为 \(x,x+d_1,x+d_1+d_2,...,x+d_1+d_2+..+d_{n-1}\)
- 则数列的和 \(x + (x+d_1) + (x+d_1+d_2) + ... + (x+d_1+d_2+..+d_{n-1}) = S\)
- 即 \(nx + (n-1)d_1 + (n-2)d_2 +..+ d_{n-1} = S\),且除了x,其余部分都是已知的
- 则 \(x=S-[(n-1)d_1 + (n-2)d_2 +..+ d_{n-1}] / n\)
- 即对于每一序列D:\(d_1,d_2,..,d_{n-1}\),满足表达式F:\((n-1)d_1 + (n-2)d_2 +..+ d_{n-1}\) % n = 0,则惟一对应一个x
- 为求合法整数序列的个数,需要求合法序列D的个数。
2.DP -背包模型
- 因为每一个\(d_i\)都是等价的,所以F可以转化为\((d_1 + 2d_2 +..+ (n-1)d_{n-1}\) % n = 0
- f[i , j]:i表示已经取了前i个d ,j表示F当前的余数。
- 假设f[i ,j] = f[i-1, c],
- 对于\(d_i = a\)有:i·a % n = j - c 则c = (j - i·a) % n; 对应的 c = (j + i·a) % n

代码:
#include <iostream>
using namespace std;
const int N = 1010, MOD = 100000007;
int f[N][N];
//求满足数学上定义的余数 - 余数一定为正数
int get_mod(int a,int b)
{
return (a % b + b) % b;
}
int main(void)
{
int n,s,a,b;
cin >> n >> s >> a >> b;
//边界处理:一项di都不取,则只有余数为0,才有一种方案
f[0][0] = 1;
for(int i = 1; i < n; i++)
for(int j = 0; j < n;j++)
f[i][j] = (f[i-1][get_mod(j + i * b, n)] + f[i-1][get_mod(j - i * a, n)]) % MOD;
//这里S % n 要改成 get_mod(s,n),防止s是负数
cout << f[n - 1][get_mod(s,n)] << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号