对于复数域的矩阵A, (n阶），应当明白这个矩阵的特征多项式（n次）一定是有n个解的，那么就有以下的结论：
如果对矩阵A有一个特征值λ0，对应其特征向量α，
有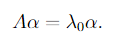
，那么可以推出
。
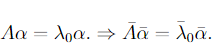分解A = B + Ci， α = β + γi， 定义A，B， C中元素用a, b, c,表示， α， β， γ的坐标对应分量用x， y， z 表示；
于是就有： aij = bij +cij * i; xj = yj + zj * i; 那么就有对于任意的A和α， 针对复数域上的计算，有Aα = （∑a1j*xj, ∑a2j*xj, ……， ∑anj*xj） = ( ∑(b1j + c1j*i)(yj + zj*i), ……∑(bnj + cnj*i)(yj+zj*i)), 不难看出把上面的式子中的加号变成减号，我们可以发现一个比较有用的结论 :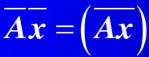
, （一个矩阵的共轭）乘上（一个向量的共轭）等于（
这个矩阵乘上这个向量）的共轭 那么对于上面的式子A α = λ0 * α，有同时对左右进行共轭运算（共轭可以看成是一个映射或者函数），则有了这样的结论。（把λ0看成λ0乘上单位矩阵I）。
又有若A为实数矩阵的话，有A等于A的共轭，那么就可以看到一个实数矩阵如果有一个复数特征值，那么其共轭值也是A的特征值，两个共轭特征值的特征向量也共轭。
注：这里矩阵和向量的共轭都是指把虚数部分的系数取相反数。
欧式空间是定义了夹角和内积的线性空间。
定义内积为一个线性空间V到数k的函数， （α， β）= α·β = α * β^T , (乘法是矩阵乘法，点乘是内积）
正交矩阵也有定义： 若有A*AT = I ， 那么A即为正交矩阵，正交矩阵的行向量组和列向量组都是单位正交向量组，且线性无关。
正交：（α， β） = 0， 两者正交。
因为标准正交基总是便于我们进行一些计算，（比如平面和立体直角坐标系）， 我们总希望把映射定义在一个标准正交基上，于是总希望找到正交相似的对角矩阵，这个矩阵不仅能够满足我们对描述映射的简单化，更能够使得对应的这些特征向量
求正交矩阵比较好的办法，先通过特征值找到特征向量，然后用特征向量进行施密特正交化（Schmidt），如果是对称矩阵，则对其中不同的特征值下的特征向量组分别进行正交化即可.
有几个结论： 1. 实对称矩阵一定有n个实数特征值
2. 实对称矩阵属于不同特征值的特征向量一定是正交的
3.实对称矩阵一定正交相似于对角矩阵
双线性函数：定义在V*V 到数域K的映射（函数），若有对任意的α，β，γ属于V， f（α，kβ+γ）=k*f（α，β）+f（α，γ）， f（kα+γ， β）= kf（α，β）+f（γ， β），（对两个分量都是线性映射的关系）
则f为一个V*V上的双线性函数，由于线性空间和线性映射的特性，一个双线性函数完全V的基向量所决定。
注：这里的X和Y由于是坐标，他们一定是列向量，也就是说X^T * A * Y最终得到的是一个1*1的函数，行向量乘矩阵乘列向量最终得到了一个数（函数）而不是函数矩阵，这里要千万注意。
和映射一样，同一个双线性函数可能有不同的度量矩阵，表示的是同一个函数（也就是说对两个向量α， β，尽管两个坐标可能发生变化，但是这两个向量作为自变量是不变的，所以函数值事实上也不会变）
这里还引入非退化线性替换的定义：
这个地方结合线性替换就是更换一个基来表示同一个向量（见对线性映射的理解）本来二次型X^T * A * X 看起来很不标准，并不像我们学过的标准形式的圆，椭圆，球，椭球那样一眼就能判断几何形状，那么这里我们可以通过更换基的方式平移或者拉伸坐标系，这样就可以转化非标准形式的二次型为标准形式的二次型，方便我们进行计算和分析，线性变换是指如何把向量坐标X通过基的变换变成另一个基下的坐标Y，过程是乘一个矩阵P， 有Y = P*X， 个人理解非退化线性替换是找到一个线性变换，使得这个变换的结果是X， 也就是X = P * Y, 在这种情况下二次型X^T * A * X = YT * PT * A * P *Y, 不难看出在Y所在的基下对应的度量矩阵是PT * A * P， 而我们知道，实对称矩阵是一定可以正交对角化的，也就是说我们能够找到一个对角矩阵diag， 使得PT * A * P = diag。 这样通过非退化线性替换我们就能够通过改换基把二次型标准化（注意线性替换是找到一个线性变换也就是把X变成线性变换的形式，找到变换之前的坐标Y）
证明思路： 对任意两个个向量分别用两个基来表示求对应的矩阵。可以得出定理。
要分清坐标向量和映射对应矩阵的左乘右乘！（重点就在于不同的坐标表示相同的向量，也就表示了相同的函数）
将合同与相似类比，就发现双线性函数也就是一种映射。
P：对任意β，f（α1，β）=0.
Q： 对任意α， f（α，β1）=0
满足p的所有α1构成的集合称为f的左根， radL f
满足q 的所有β1构成的集合称为f的右根，radRf
如果f的左右根都是零子空间，那么f就称为非退化的，就是仅有零的左根和右根，可以类比可逆矩阵（非奇异矩阵）
度量矩阵可逆，则f非退化。
证明提示：只考虑对V的基α1到αn的双线性函数的处理， 即定义一个基α1~αn，对应的有f（αi ， αj） = f（αj， αi），所以得证。
二次型就是一种双线性函数的特例，二次型是一个f（α，α），不难看出，如果α是一个坐标向量的话，这个f（α，α）就变成了一个二次齐次多项式，我们把这种多项式叫做二次型，并且写成X^T *A * X的形式，这里要注意，一个A可以确定一个二次型，但是一个二次型可能得到不同的矩阵A， 比如f = x1^2 + x^2,它可以是形如
1 0 1 -1
0 1 这样的矩阵，也有可能是 1 1 这样的矩阵，但是如果规定A是一个对称矩阵，那么就可以唯一确定这个A了，二次型在高等代数中指可以建立矩阵和多项式的一一对应关系的对应多项式，也就是说如果没有声明，则大部分二次型都指对称矩阵所对应的二次齐次多项式。
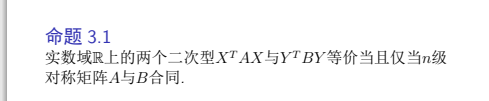
正定矩阵即使满足对任意向量α， α^T *A* α > 0 的矩阵，可以看到，正定矩阵和正定二次型相互对应。
我们应当注意到正定二次型比较实际的应用就是内积，在欧式空间中的内积计算往往在选定了一组基之后就是一个对坐标向量进行二次型求解的过程。
