求最大公约数伪代码

求最大公约数伪代码

关于辗转相除法

什么是两个数的最大公约数的欧几里得算法（辗转相除法）？

辗转相除法， 又名欧几里德算法（Euclidean algorithm），是求最大公约数的一种方法。它的具体做法是：用较大数除以较小数，再用出现的余数（第一余数）去除除数，再用出现的余数（第二余数）去除第一余数，如此反复，直到最后余数是0为止。如果是求两个数的最大公约数，那么最后的除数就是这两个数的最大公约数。

算法链接

(https://blog.csdn.net/qinzaoxiaozhu/article/details/113917610)

算法说明

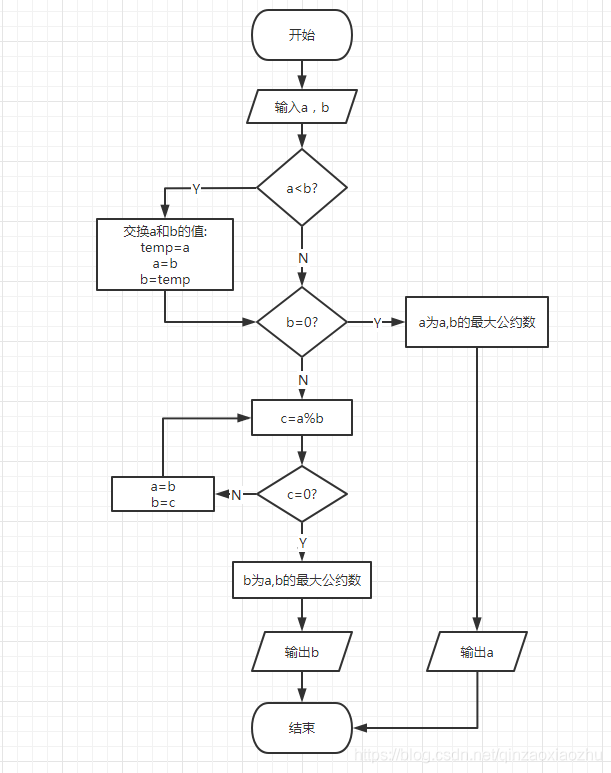
输入a,b
-判断a是否小于b ①
若是，则交换a，b的值，进入下一步
若不是，进入下一步
-判断b是否等于0 ②
若是，则a为a，b的最大公约数，输出a
若不是，令c为a除以b的余数，进入下一步
-判断c是否为0 ③
若不是，则将b赋值给a，将c赋值给b，重复②中的“不是”的步骤
若是，则b为a，b的最大公约数，输出b

辗转相除法的伪代码

input a，b
while a < b
  temp = a
  a = b  
  b = temp

if b = 0
  print a
else
  c = a % b

    while c != 0
      a = b
      b = c

  print b

手动计算验证