分类器训练结果之混淆矩阵分析

机器学习尤其针对分类器这，有各种指标来评判最终的模型效果，以前总听说混淆矩阵，也不知道到底干啥的，反正听着就让人很混淆，后来看了网上两篇文章，自己又实践一下，基本搞明白了，我给它起了个新名字，叫“分类结果统计矩阵“，非TM拽那么高大上的名字干啥，听着都让人望而却步了，还有一些机器学习必备装B名词，梯度爆炸、深度神经网络、反向传播，都是装B名词，其实只有明白人才知道都是前辈们几十年前搞烂的东西，唉，通俗点不好么？？？

下面我把这两篇文章转载过来，地址都放在了每篇文章的后面了。

1、在机器学习领域，混淆矩阵（confusion matrix），又称为可能性表格或是错误矩阵。它是一种特定的矩阵用来呈现算法性能的可视化效果，通常是监督学习（非监督学习，通常用匹配矩阵：matching matrix）。其每一列代表预测值，每一行代表的是实际的类别。这个名字来源于它可以非常容易的表明多个类别是否有混淆（也就是一个class被预测成另一个class）。

假设有一个用来对猫（cats）、狗（dogs）、兔子（rabbits）进行分类的系统，混淆矩阵就是为了进一步分析性能而对该算法测试结果做出的总结。假设总共有 27 只动物：8只猫， 6条狗， 13只兔子。结果的混淆矩阵如下图：

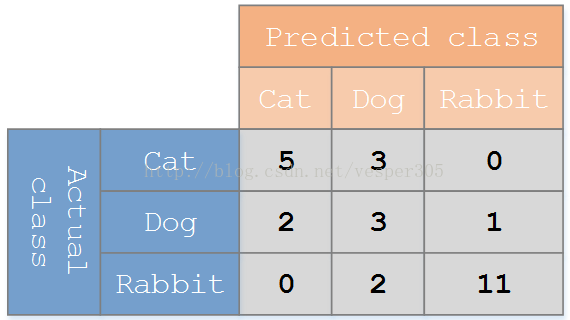
PS：这个图对应的就是sklearn的混淆矩阵

在这个混淆矩阵中，实际有 8只猫，但是系统将其中3只预测成了狗；对于 6条狗，其中有 1条被预测成了兔子，2条被预测成了猫。从混淆矩阵中我们可以看出系统对于区分猫和狗存在一些问题，但是区分兔子和其他动物的效果还是不错的。所有正确的预测结果都在对角线上，所以从混淆矩阵中可以很方便直观的看出哪里有错误，因为他们呈现在对角线外面。

在预测分析中，混淆表格（有时候也称为混淆矩阵），是由false positives，falsenegatives，true positives和true negatives组成的两行两列的表格。它允许我们做出更多的分析，而不仅仅是局限在正确率。准确率对于分类器的性能分析来说，并不是一个很好地衡量指标，因为如果数据集不平衡（每一类的数据样本数量相差太大），很可能会出现误导性的结果。例如，如果在一个数据集中有95只猫，但是只有5条狗，那么某些分类器很可能偏向于将所有的样本预测成猫。整体准确率为95%，但是实际上该分类器对猫的识别率是100%，而对狗的识别率是0%。

对于上面的混淆矩阵，其对应的对猫这个类别的混淆表格如下：

假定一个实验有 P个positive实例，在某些条件下有 N 个negative实例。那么上面这四个输出可以用下面的偶然性表格（或混淆矩阵）来表示：

公式定义如下：

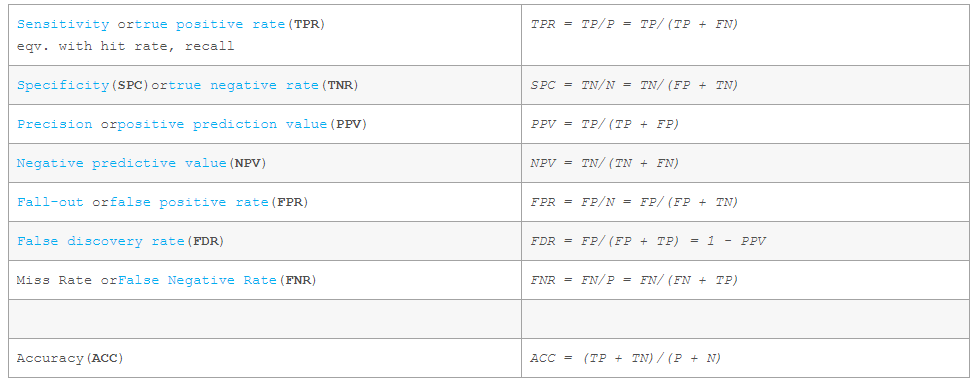
转载自https://blog.csdn.net/vesper305/article/details/44927047

2、我理解上的混淆矩阵就是一个分类器对于正反例（假设是二分类，多分类也类似）的混淆程度。

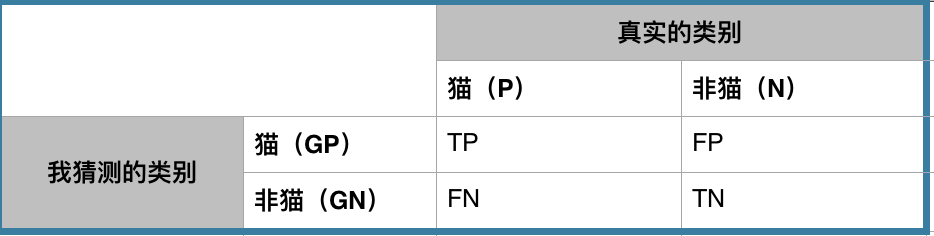
我有见过两种不同混淆矩阵，主要区别是对于真实的类别和猜测的类别的位置互换。其实本质上没有大区别的，看每一个人的习惯。这里采用wikipedia的格式。

初学者一般看到这个矩阵的描述就晕了。怎么那么多字母？TP，FP，FN，TN是什么？就算告诉你TP=True Positive的意思，你也要晕半天，更别说之后的各种度量公式。如PPV， NPV，Recall， F1，ROC等等。

怎么生成混淆矩阵
假设测试数据中我有5个猫图片和8个非猫图片的例子。首先在猫(P)的地方的P填写5， 非猫(N)的地方的N填写8。说明测试数据中真实的类别猫有5例，非猫有8例。

在TP，FP，FN，TN的地方都填上0。

接下去从13例测试例子中一例一例的问分类器（也就是我），比如拿一例猫图片问我，我回答是猫，那么在TP的地方就加1。如果我回答了非猫，那么在FN的地方就加1。再比如拿一例非猫的图片问我，我回答是非猫，那么在TN的地方加1，如果我回答了猫，那么在FP的地方加1。

等13例都问完之后，那么整个混淆矩阵也就完成了。如下图：

基本用语的解释
condition positive (P) = 测试数据中正例的数量。此处是猫=5。
condition negatives (N) = 测试数据中反例的数量。此处是非猫=8。
true positive (TP) = 是正例，且很幸运我也猜它是正例的数量。此处4表示有4张图片是猫，且我也猜它是猫。TP越大越好，因为表示我猜对了。这个时候如果你质问我猫不是5张图片吗？那么别急，重新看看TP的定义。然后再看看FN的定义。
false negtive (FN) = 明明是正例，但很不幸，我猜它是反例的数量。此处1表示有1张图片明明是猫，但我猜它非猫。FN越小越好，因为FN说明我猜错了。现在来看5张猫图片是不是全了。其中4张猫我猜是猫，1张猫我猜非猫。
true negative (TN) = 是反例，且很幸运我也猜它是反例的数量。此处5表示有5张图片是非猫，且我也猜它是非猫。TN越大越好，因为表示我猜对了。
false positive (FP) = 明明是反例，但很不幸我猜它是正例的数量。此处3表示有3张图片是非猫，但我猜它是猫。FP越小越好，因为FP说明我猜错了。

小总结：
正对角线的数字越大越好，因为都是我猜对的次数。
其他地方越小越好，因为都是我猜错的次数。
竖的列加起来就是测试数据中猫和非猫的各自真实的数据量。
横的行加起来就是我猜猫和我猜非猫的次数。
补充：GP的意思就是I guess positive，注意GP是我自己定的，不是官方标准。GN就是I guess negtive。

各种度量
这里开始才是重点，可能要配合一定的实践，才能更加深刻的领悟其中的奥妙。

sensitivity, recall, hit rate, or true positive rate (TPR)
以上的几种说法都是一个意思。硬翻译的话是灵敏度，召回度，命中率或者是正例中猜对的比例。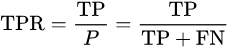

* 理解1：范围是0-1， 猫的例子中sensitivity=4/5=0.8
* 理解2： 分母是真实正例的总数，和你的猜测值无关
* 理解3： 分子是你猜正例且猜对的次数，和其他都无关。反例你猜对的再多和分子没有关系。
* 理解4： 如果对于所有的测试数据，你都猜是正例，则该值肯定是1。假设猫的例子，你如果13张图片都猜是猫，那么你的TRP = 5／5 = 1。由于测试数据中存在非猫，所以你对于猫过于灵敏，这大概也是为什么sensitivity的命名原因。recall（召回）的原因是总共有5只猫，你把5只猫都找对了，所以叫做召回了所有的猫。
* 理解5： 该值越大，表示分类器对正例越灵敏，越能找全所有的正例。
* 理解6： 好的分类器该值要大，仅该值大的分类器不一定就好。单独该值无法判断分类器的优劣。因为好的分类器不但要对正例灵敏，还要对反例专一。

specificity or true negative rate (TNR)
以上两种说法也是一个意思。specificity翻译过来是特异度，专一度。我理解是灵敏度的反义词。就是不要看到任何例子都猜是正例，要有自己的见解和专一。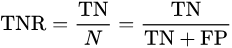

* 理解1：范围是0-1， 猫的例子中specificity=5/8=0.625
* 理解2： 分母是真实反例的总数，和你的猜测值无关
* 理解3： 分子是你猜反例且猜对的次数，和其他都无关。正例你猜对的再多和分子没有关系。
* 理解4： 如果对于所有的测试数据，你都猜是反例，则该值肯定是1。假设猫的例子，你如果13张图片都猜是非猫，那么你的TNR = 8／8 = 1。由于测试数据中存在猫，所以你对于非猫过于专一，这大概也是为什么specificity的命名原因。
* 理解5： 该值越大，表示分类器对反例越专一。
* 理解6： 好的分类器该值要大，仅该值大的分类器不一定就好。单独该值无法判断分类器的优劣。因为好的分类器不但要对反例专一，还要对正例灵敏。

precision or positive predictive value (PPV)

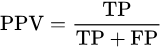
PPV也就是正例的precision。
大家经常会看到precision和recall经常出现，因为precision和recall的综合表现，可以基本揭示分类器对于正例的好坏程度。

理解1： 整个的意思就是你总共猜了几次是猫（分母），其中猜对多少次（分子）。猫的例子中PPV = 4/7 = 0.57。
理解2： 如果分类器比较保守，它只对最有把握的一张图片说是猫（假设这种确实是猫），而说其他都不是猫。那么它的precision就是100%。想想公式，你总共猜了几次是猫是分母，其中猜对了多少次是分子。
理解3：13张图片中总共5只是猫，如果你为了找全猫，从而猜说13张都是猫，那么你的recall（召回率）或者sencitivity（敏感度）会非常高，等于1。但是牺牲的是precision，因为你猜了13次猫会作为分母，而猜对的5次是分子，所以precision = 5/13 = 0.38。（叫你瞎猜！）
理解4： 一般分类器猜正例比较激进，那么recall会比较好看，但是precision会比较难看，如果分类器猜正例比较保守，那么precision会比较高，但是recall就不一定高。

negative predictive value (NPV)

NPV完全就是和PPV相对的东西了。PPV是分类器猜正例的正确率，NPV是分类器猜反例的正确率。

理解1：整个的意思就是你总共猜了几次是非猫（分母），其中猜对多少次（分子）。猫的例子中NPV = 5/6 = 0.83。
理解2：PPV + NPV 不等于1。想想极端例子，13张图我全猜猫，PPV=1，NPV=0/0没有意义。你都不猜反例，让我怎么评价你的猜反例的正确率。

accuracy (ACC)

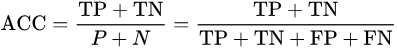
整体的正确率。即猜对的次数（无论是正例还是反例）除以总测试数据的总数。

看几个混淆矩阵

完美的分类器

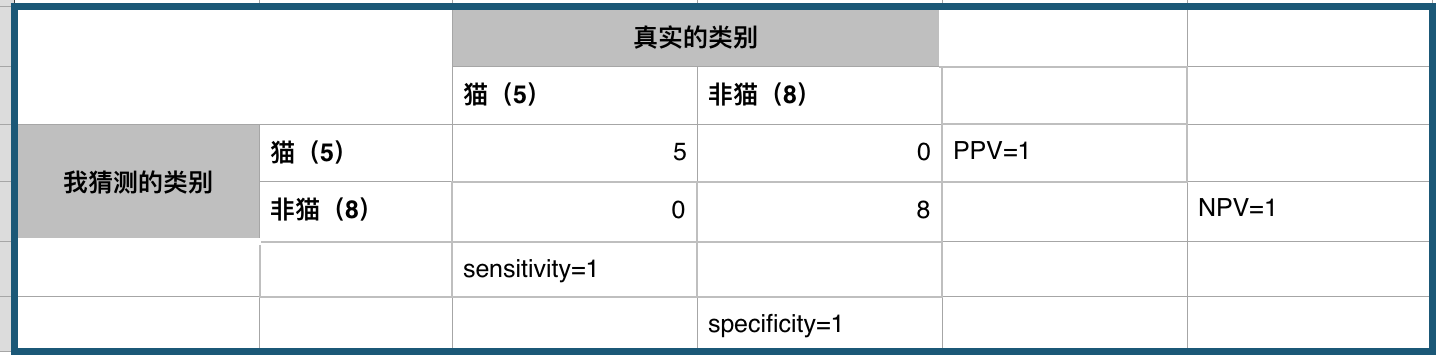
P = 5
N = 8
TP = 5
FP = 0
FN = 0
TN = 8
sensitivity = 5/5 = 1 # 正例找的够全或者说我不会看漏正例
specificity = 8/8 = 1 # 反例找的也够全或者说我不会看漏反例
PPV = 5/5 = 1 # 猜正例的时候一猜一个准或者说我猜它正例，它就不会是反例
NPV = 8/8 = 1 # 猜反例的时候一猜一个准或者说我猜它反例，他就不会是正例
acc = 13/13 = 1 # 全部猜对

激进的分类器

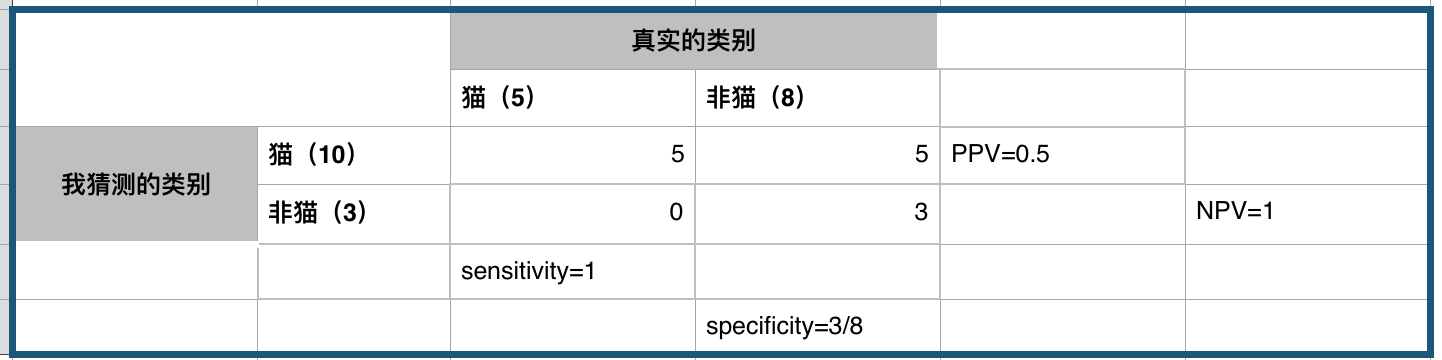
P = 5
N = 8
TP = 5
FP = 5
FN = 0
TN = 3
sensitivity = 5/5 = 1 # 正例找的够全或者说我不会看漏正例
specificity = 3/8 # 反例找的不够全
PPV = 5/10 = 0.5 # 猜正例的时候有一半几率猜对
NPV = 3/3 = 1 # 猜反例的时候一猜一个准或者说我猜它反例，他就不会是正例
acc = 8/13 # 总共猜对8例，猜错5例，比随机猜好一点点
转载自：https://blog.csdn.net/leon_wzm/article/details/77524694