二维凸包学习笔记
二维凸包学习笔记
初识二维凸包
- 凸包是计算机图形学中的一个概念。
- 但是讲大白话的话就是:
- 给你一堆点,然后用一个多边形把这些点圈起来,这个多边形就是凸包。(当然多边形周长是最小的。)
- 求凸包有好多种方法,\(Graham\)法较为常用。
- \(Graham\)葛立恒,曾经是美国数学学会\((AMS)\)主席。
前置知识
- 简单平面几何知识
- 叉积的概念或基础的线性代数中的行列式知识
Graham算法
本质
- \(Graham\)扫描算法维护一个凸壳,通过不断地在凸壳中加入新的点和取出影响凸性的点最后形成凸包。
- 凸壳:凸包的一部分。
算法流程
\(1:\)排序
- 选择一个\(y\)值最小的点(如果有相同的\(y\),则选择\(x\)最小),记为\(P_1\)。
- 那其实就相当于选了一个最下边的点,而且这个点一定在凸包的边上。
- 剩下的点按照极角的大小逆时针排序,编号为\(P_2\)~\(P_n\)
\(2:\)扫描
- 逆时针顺序扫描\(P_1\)$P_2$,$P_2$\(P_3,...,P_n\)~\(P_1\),如果扫描的那条线是逆时针,则确定他是凸包的点,否则不是。
- 这么说比较抽象,直接来看过程图示模拟。
过程模拟
-
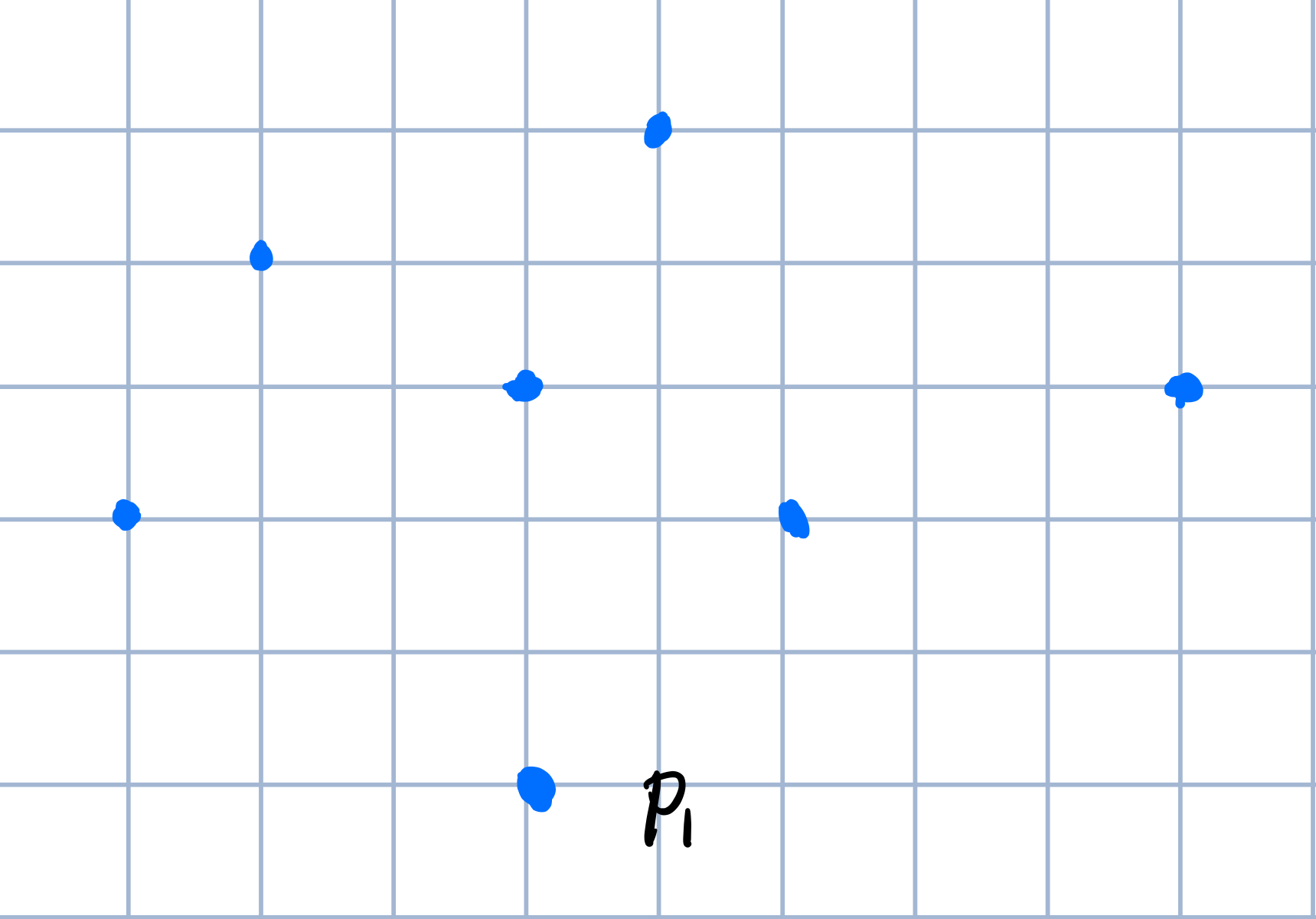
首先我随机设置了一些点,如图所示。
-

-
之后我先取\(y\)值最小的点,很显然是最下方的那个点,将他设置为\(P_1\)。
-
-
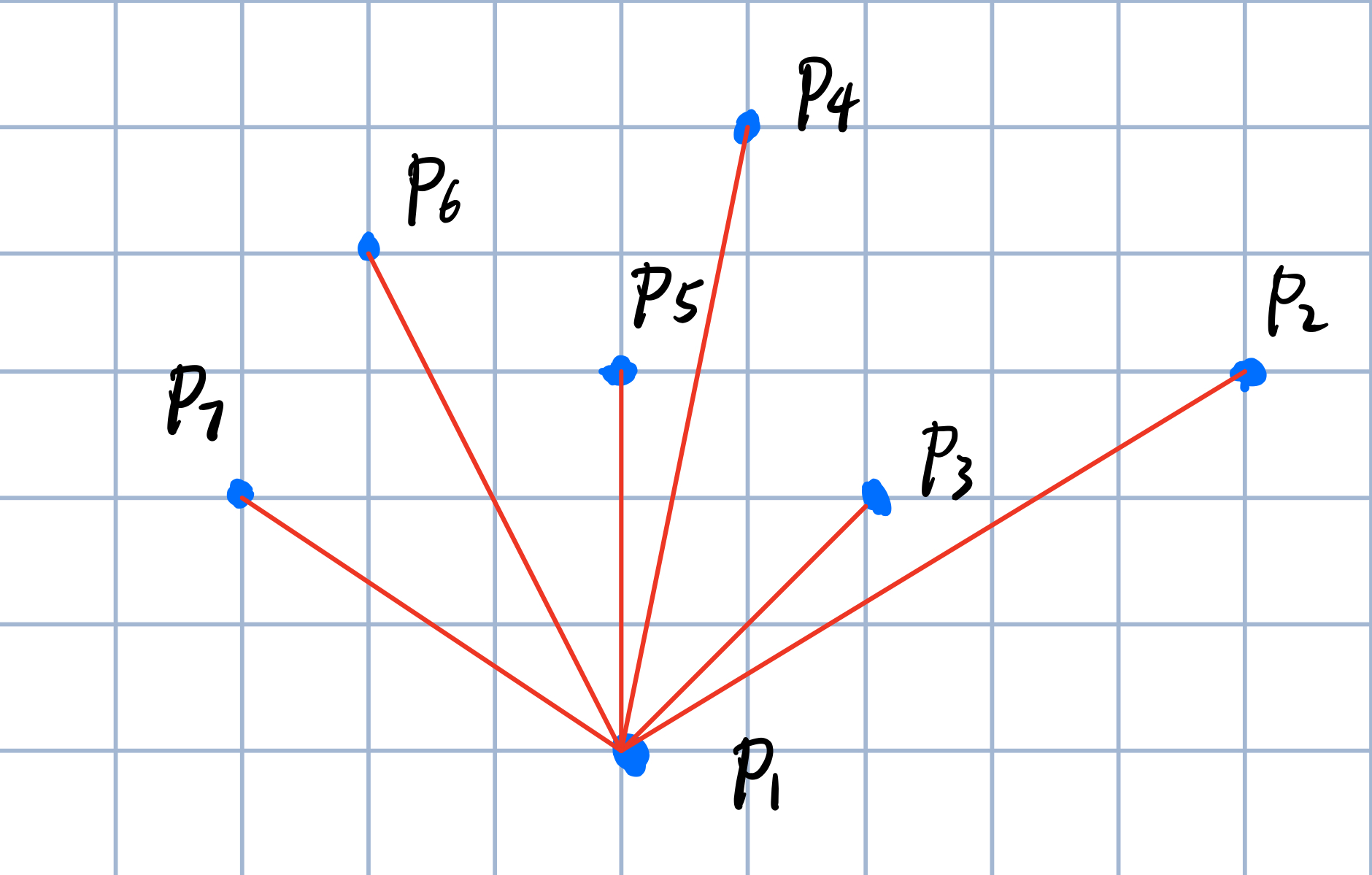
之后按照极角排序
-
-
这时候我们就给点编好号了
-
我们先扫描\(P_1\)到\(P_2\)。
-

-
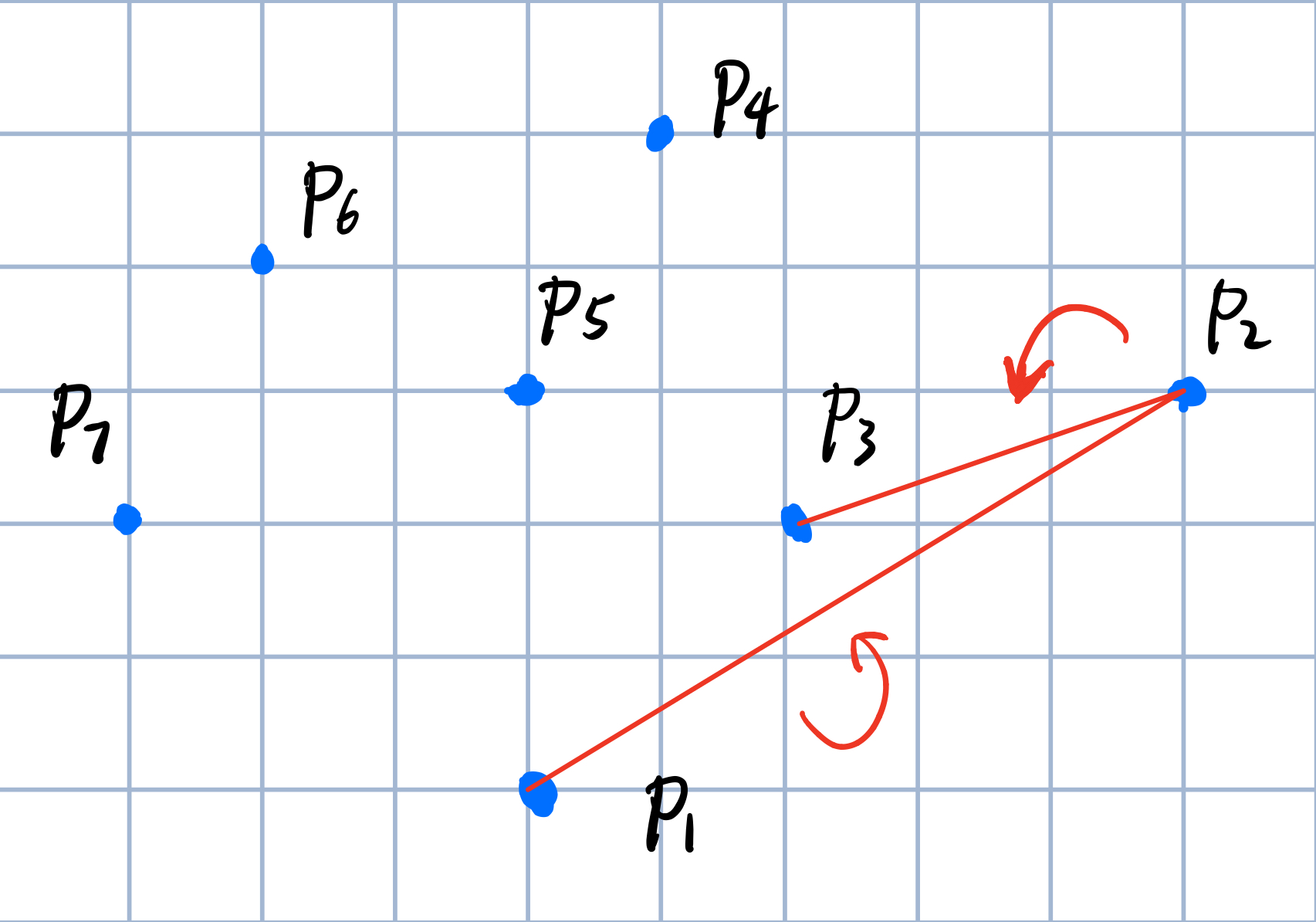
然后扫描\(P_2\)~\(P_3\)
-
-
我们发现新的这一条先也是逆时针的,所以我们将\(P_3\)候选。
-
当然对于整幅图,\(P_3\)不在凸包上,但是对于\(P_1,P_2,P_3\)来讲,\(P_3\)在凸包上。
-
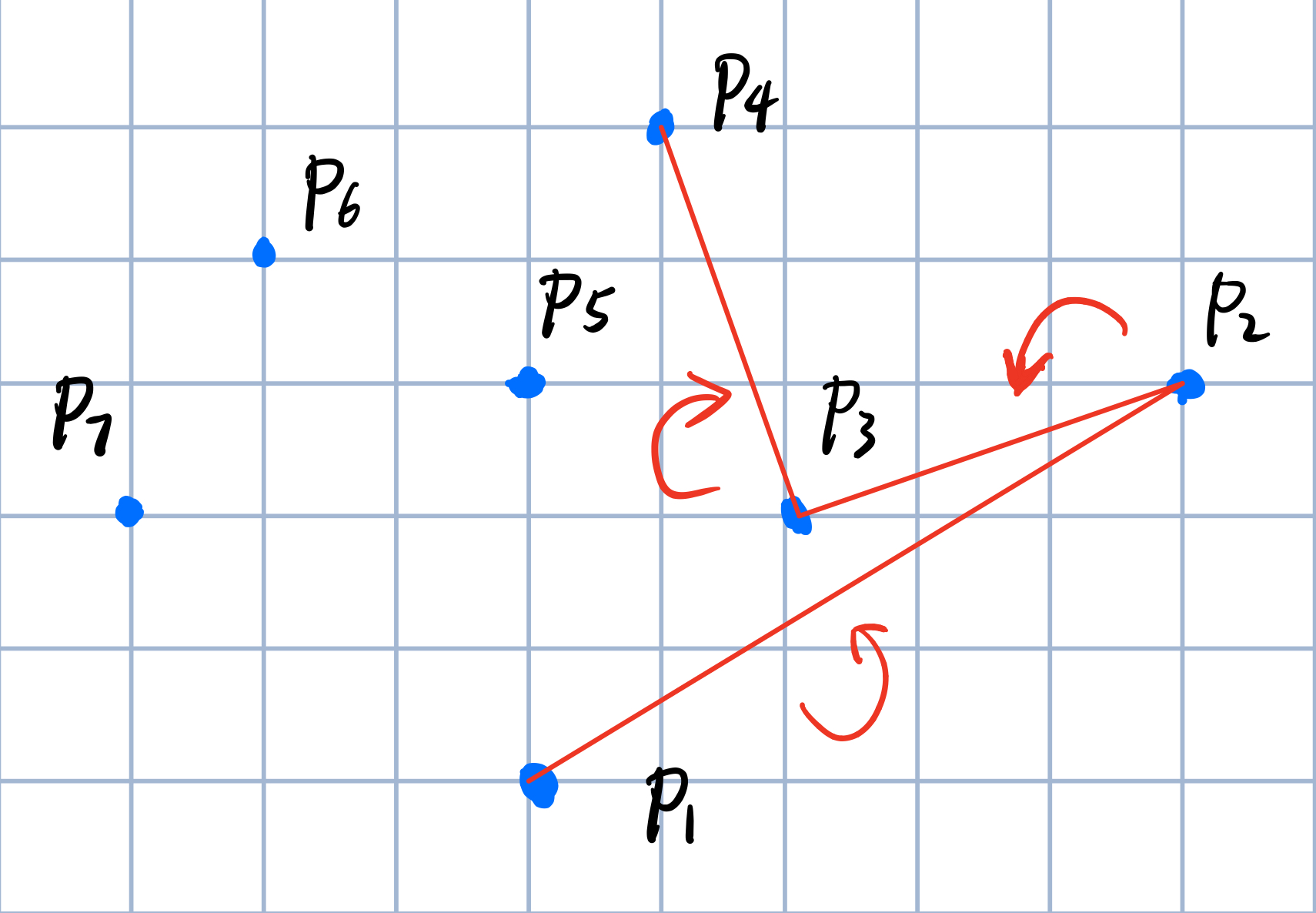
接下来扫描\(P_3\)~\(P_4\)
-
-
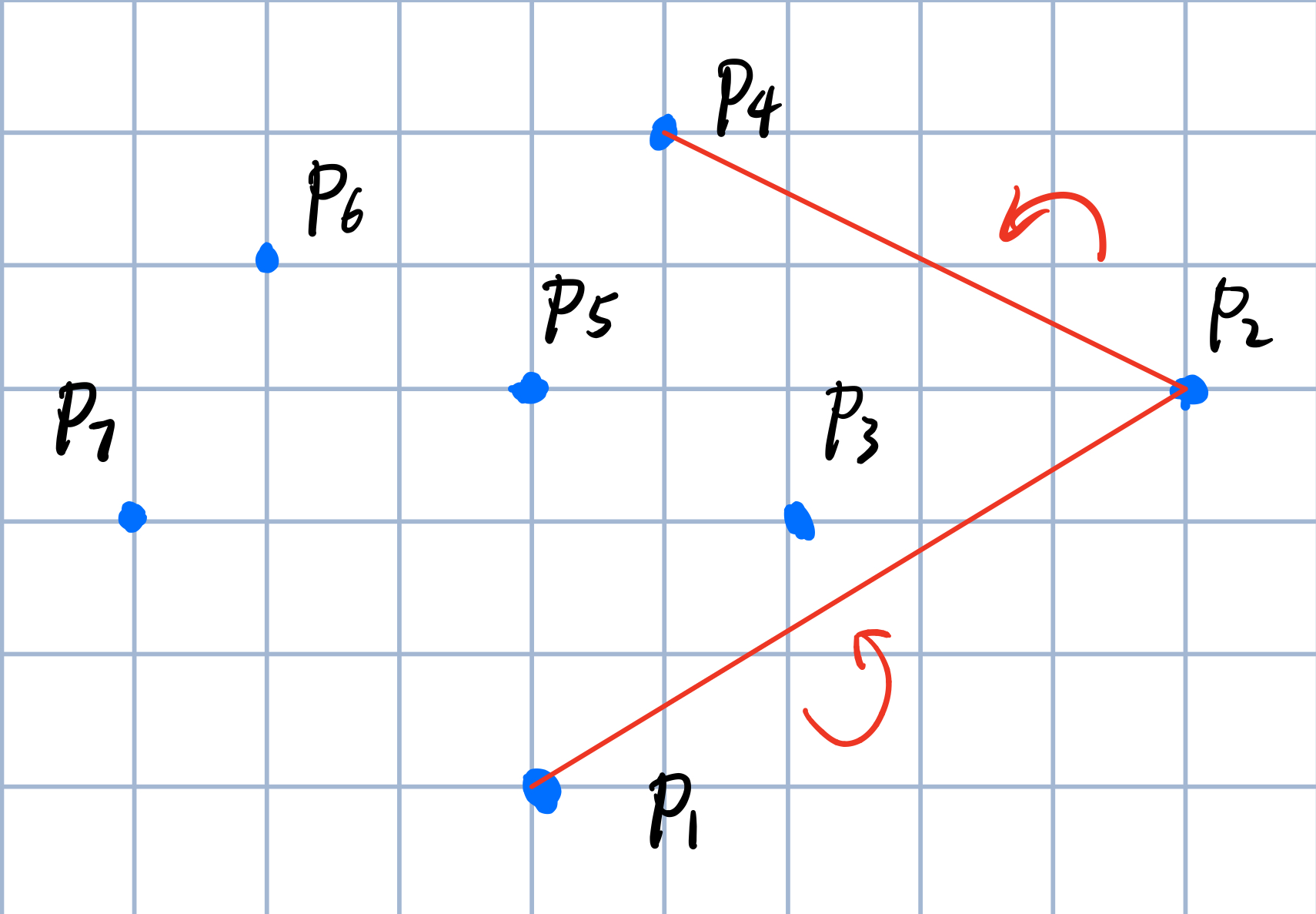
我们发现新的扫描的\(P_3\)$P_4$顺时针了,说明$P_3$不应该候选,$P_4$应该候选,所以将$P_2$\(P_3\)删除后加入\(P_2\)~\(P_4\)。
-
-
之后我们看\(P_4\)到\(P_5\)
-
-
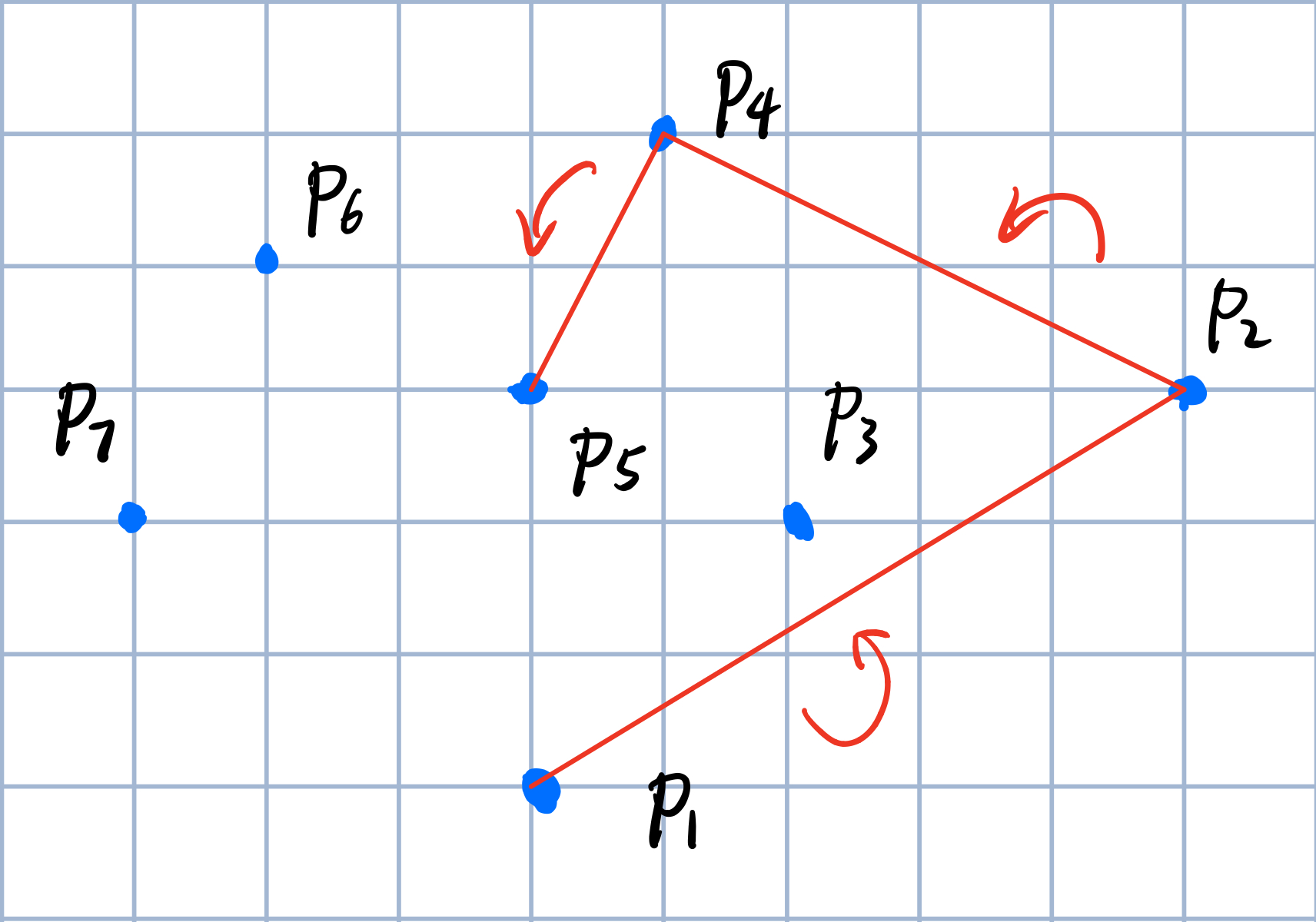
这时候是逆时针,将\(P_5\)候选。
-
接下来扫描\(P_6\)
-

-
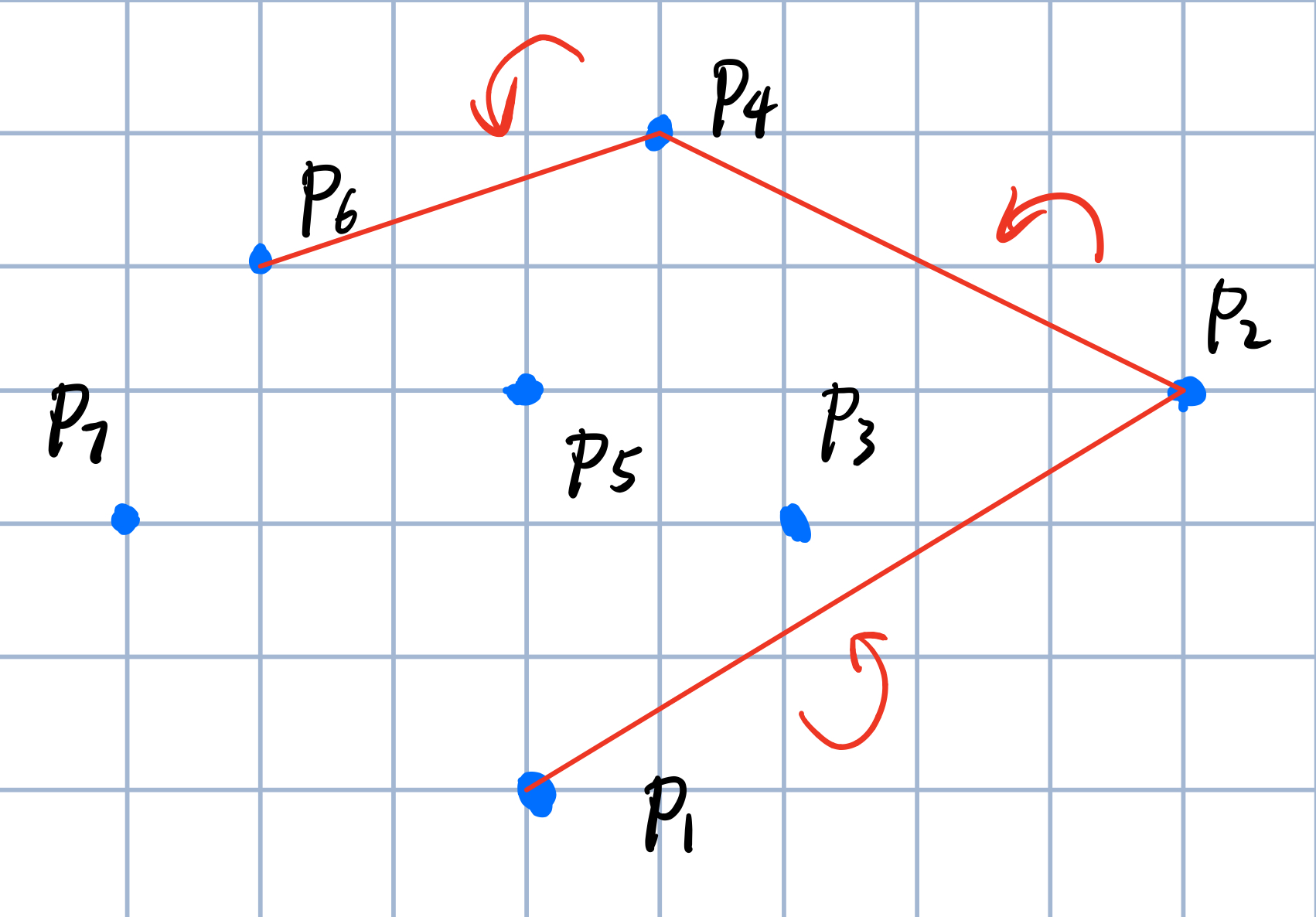
这时候顺时针了,所以\(P_5\)不应该候选,删除\(P_4\)$P_5$后加入$P_4$\(P_6\)。
-
-
然后看\(P_7\)
-

-
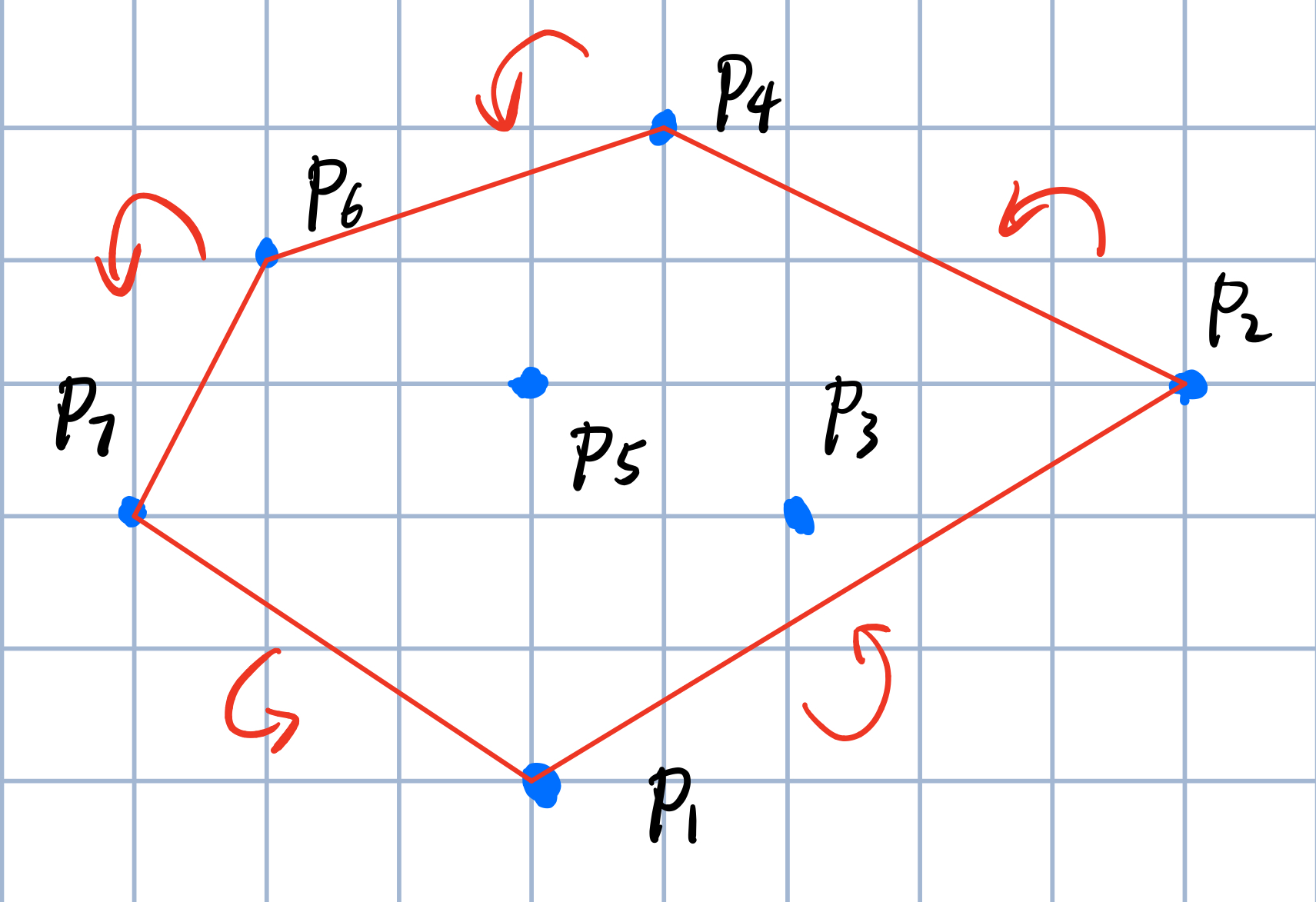
逆时针,\(P_7\)候选
-
最后连接\(P_1\)回来即可
-
代码实现
-
我们发现每次扫描一个出点的时候都是先让他可能候选,当他下一条出的边依然是逆时针就将他确定候选,所以这时候用一个栈来保存点就可以了。
-
当他可能候选的时候入栈,如果不是的话\(pop\)栈即可。
-
对于顺时针还是逆时针,我们运用叉积来判断。(如果这里学过线性代数应该就能很快理解代码里的VP函数)
-
模板题:洛谷2742二维凸包
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n;
struct Node{
double x, y;
}p[maxn], s[maxn];
//p是点 s数组模拟栈
//二维向量叉积公式a(x1, y1), b(x2, y2)
//a × b = (x1y2 - x2y1)
double vp(Node a1, Node a2, Node b1, Node b2){
//VectorProduct 向量叉积
return (a2.x-a1.x)*(b2.y-b1.y) - (b2.x-b1.x)*(a2.y-a1.y);
}
double dis(Node a, Node b){
//返回两点距离
return sqrt((b.y-a.y)*(b.y-a.y)+(b.x-a.x)*(b.x-a.x));
}
bool cmp(Node a, Node b)
{
double tmp = vp(p[1], a, p[1], b);
if(tmp > 0) return 1;
//叉积为0 说明两点共线
//让离远点远的点排在靠后的地方
if(tmp == 0 && dis(p[0], a) < dis(p[0], b)) return 1;
return 0;
}//极角排序
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)
{
scanf("%lf%lf", &p[i].x, &p[i].y);
if(i != 1 && (p[i].y < p[1].y || (p[i].y == p[1].y && p[i].x < p[1].x))) //让p1保存最靠下的点
{
double tmp;
tmp = p[1].y; p[1].y = p[i].y; p[i].y = tmp;
tmp = p[1].x; p[1].x = p[i].x; p[i].x = tmp;
}
}
sort(p+2, p+1+n, cmp);
int cnt = 1; //stack.size()
s[1] = p[1];
for(int i = 2; i <= n; i++)
{
//判断上一个点会不会不合法
while(cnt > 1 && vp(s[cnt-1], s[cnt], s[cnt], p[i]) <= 0)
cnt--;
s[++cnt] = p[i];
}
s[cnt+1] = p[1]; //最后回到起点
//此时栈中存的是所有凸包上的点
double ans = 0;
for(int i = 1; i <= cnt; i++)
ans += dis(s[i], s[i+1]);
printf("%.2f\n", ans);
return 0;
}



