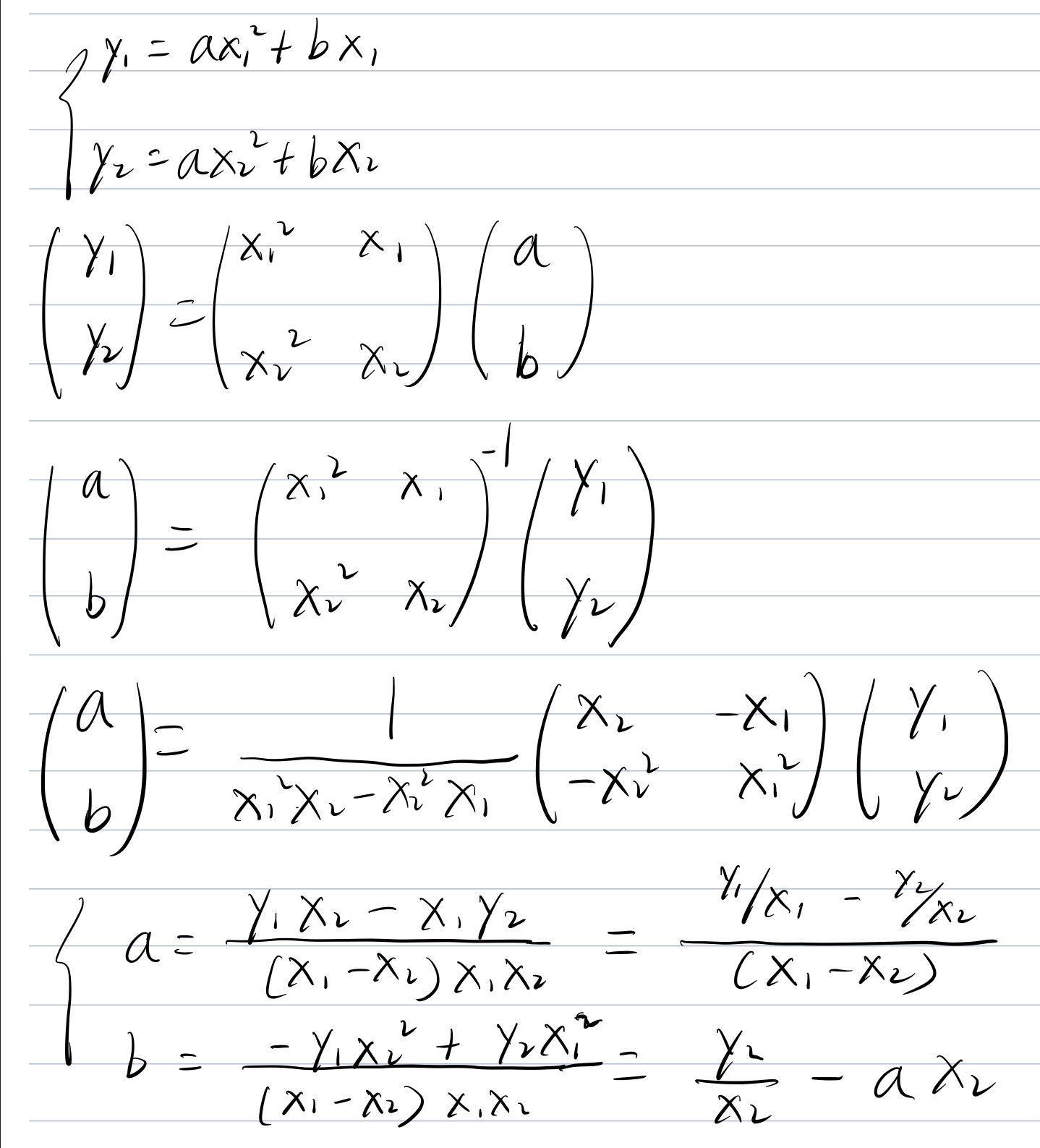luogu_2831: 愤怒的小鸟
洛谷2831:愤怒的小鸟(状压\(dp\))
题意:
- 在二维平面上给定\(n\)个点\((1\leq n\leq18)\)。
- 其中每个点用\((x_i,y_i)\)表示\((0<x_i,y_i<10)\),输入均保留两位小数。
- 求最少多少个经过原点的抛物线贯穿所有点。
输入格式:
- 第一行输入一个整数\(T\)代表有T组测试样例。
- 第二行输入两个整数\(n\)和\(m\)分别代表有多少个点和\(m\)的限制(见题意)。
- 其实这个\(m\)没什么用
- 接下来\(n\)行输入每行输入两个浮点数表示点的坐标。
输出格式:
- 输出\(T\)个整数表示答案。
思路:
-
这个数据范围不是爆搜就是状压。
-
首先题面说明必须要经过原点,所以原本三点确定抛物线,现在我们可以用两个点就能确定一条抛物线了。
-
所以可以用\(line(i,j)\)表示穿过\(i,j\)的抛物线所能经过所有点的集合。
-
再设\(f(s)\)表示在\(s\)状态下已经穿过了的点所需要的最少抛物线数。
-
当然,有:
- \(f(0)=0\)
- 枚举没有被穿过的点\(i,j\)
- \(f(s|line(i,j))=min(f(s|line(i,j)),f(s)+1)\)
- 考虑有些点可能只能用一条抛物线单独穿过,即他不能和其他点计算出合法抛物线。
- 所以还需要枚举未穿过的点对其单独穿过。
- \(f(s|(1<<(i-1)))=min(f(s|1<<(i-1)),f(s)+1)\)
- 最后答案为\(f((1<<n)-1)\)
-
需要遍历整个状态,所以有\(2^n\),同时需要枚举\(i\)和\(j\)。
-
总复杂度为\(O(Tn^22^n)\)带入\(n==18\)算一下发现稍微有点危险。
-
所以考虑优化
-
优化\(1:\)
- 当\(i\in S\)或者\(j\in S\)时没必要转移。(但这只是一个常数优化)
-
优化\(2:\)
- 对于每一个状态\(i\),我们找到他正数第一个没有被穿过的抛物线进行转移后\(break\)掉。
- 因为如果转移了第一个后面的某一个没有被穿过的点,在转移的过程中还是需要穿过第一个点。
- 所以我们每次处理第一个没被处理的点,后面的一个一个轮着转移就行了。
-
怎么判断一个点是不是在另外两个点确定的抛物线上?
-
即满足\(a,b\)的条件的时候就能判定在一条抛物线上了
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 25, INF = 0x3f3f3f3f;
int T, n, m;
int line[maxn][maxn];
int f[1<<maxn];
double x[maxn], y[maxn];
inline bool same(double x, double y){
return fabs(x - y) < 1e-6;
}
void init()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%lf%lf", &x[i], &y[i]);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
line[i][j] = 0;
//考虑ij每一种组合
for(int i = 1; i <= n-1; i++)
for(int j = i + 1; j <= n; j++)
{
if(same(x[i], x[j])) continue; //如果他们在同一列
double aa = (y[j]/x[j] - y[i]/x[i]) / (x[j]-x[i]);
if(aa >= 0) continue;
double bb = y[i]/x[i] - aa*x[i];
for(int k = 1; k <= n; k++)
if(same(aa*x[k]+bb, y[k]/x[k])) //如果他在这条抛物线上
line[i][j] |= (1<<(k-1));
}
for(int i = 0; i <= (1<<n)-1; i++) f[i] = INF; f[0] = 0;
}
int main()
{
scanf("%d", &T);
while(T--)
{
init();
for(int i = 0; i <= (1<<n)-1; i++)
{
for(int j = 1; j <= n; j++)
if(!(i&(1<<(j-1)))) //如果这里有一个没有穿过的点
{
for(int k = j; k <= n; k++) //前面的已经串好了
{
if(j == k)
f[i|(1<<(j-1))] = min(f[i|(1<<(j-1))], f[i]+1);
if(same(x[j], x[k])) continue;
//用已有的线好还是再多一条线好
f[i|line[j][k]] = min(f[i|line[j][k]], f[i]+1);
}
break;
}
}
//输出答案
printf("%d\n", f[(1<<n)-1]);
}
return 0;
}