CF959C Mahmoud and Ehab and the wrong algorithm 构造
Mahmoud was trying to solve the vertex cover problem on trees. The problem statement is:
Given an undirected tree consisting of n nodes, find the minimum number of vertices that cover all the edges. Formally, we need to find a set of vertices such that for each edge (u, v) that belongs to the tree, either u is in the set, or v is in the set, or both are in the set. Mahmoud has found the following algorithm:
- Root the tree at node 1.
- Count the number of nodes at an even depth. Let it be evenCnt.
- Count the number of nodes at an odd depth. Let it be oddCnt.
- The answer is the minimum between evenCnt and oddCnt.
The depth of a node in a tree is the number of edges in the shortest path between this node and the root. The depth of the root is 0.
Ehab told Mahmoud that this algorithm is wrong, but he didn't believe because he had tested his algorithm against many trees and it worked, so Ehab asked you to find 2 trees consisting of n nodes. The algorithm should find an incorrect answer for the first tree and a correct answer for the second one.
The only line contains an integer n (2 ≤ n ≤ 105), the number of nodes in the desired trees.
The output should consist of 2 independent sections, each containing a tree. The algorithm should find an incorrect answer for the tree in the first section and a correct answer for the tree in the second. If a tree doesn't exist for some section, output "-1" (without quotes) for that section only.
If the answer for a section exists, it should contain n - 1 lines, each containing 2 space-separated integers u and v (1 ≤ u, v ≤ n), which means that there's an undirected edge between node u and node v. If the given graph isn't a tree or it doesn't follow the format, you'll receive wrong answer verdict.
If there are multiple answers, you can print any of them.
2
-1
1 2
8
1 2
1 3
2 4
2 5
3 6
4 7
4 8
1 2
1 3
2 4
2 5
2 6
3 7
6 8
In the first sample, there is only 1 tree with 2 nodes (node 1 connected to node 2). The algorithm will produce a correct answer in it so we printed - 1 in the first section, but notice that we printed this tree in the second section.
In the second sample:
In the first tree, the algorithm will find an answer with 4 nodes, while there exists an answer with 3 nodes like this: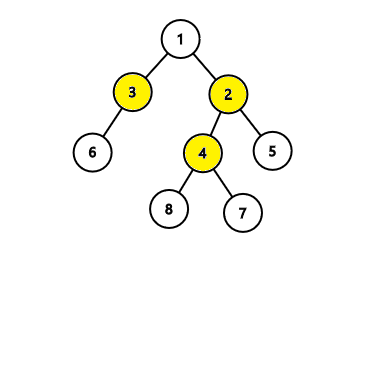 
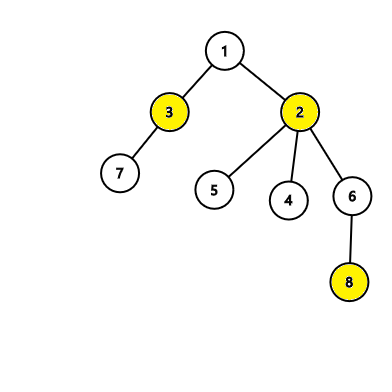
In the second tree, the algorithm will find an answer with 3 nodes which is correct:
题意：
输入一个n，代表一棵n个节点的树。有个同学提出了个猜想，他想通过删除点（删除一个点就是同时删除和它相连的所有边）来删除完所有边，他认为x=min（这棵树的奇深度的所有点的个数，这棵树的偶深度的所有点的个数），这个x就是可以删除所有边的最小的要切除的点的个数。要输出一个反例的树，然后再输出一个符合的树
思路：
可以发现1~5时，均符合结论；
当 n>=6时，我们可以这样构造：
树的深度总共就3层，而偶数层为2，奇数层为1，3。我们这样构造：
1----->3,1----->2,1------>4;
3----->5...n ；这样实际上最少操作次数为2，而该结论为3；
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 400005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline ll rd() {
ll x = 0;
char c = getchar();
bool f = false;
while (!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
while (isdigit(c)) {
x = (x << 1) + (x << 3) + (c ^ 48);
c = getchar();
}
return f ? -x : x;
}
ll gcd(ll a, ll b) {
return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }
/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
if (!b) {
x = 1; y = 0; return a;
}
ans = exgcd(b, a%b, x, y);
ll t = x; x = y; y = t - a / b * y;
return ans;
}
*/
ll qpow(ll a, ll b, ll c) {
ll ans = 1;
a = a % c;
while (b) {
if (b % 2)ans = ans * a%c;
b /= 2; a = a * a%c;
}
return ans;
}
int n;
int main()
{
//ios::sync_with_stdio(0);
rdint(n);
if (n == 1 || n == 2 || n == 3 || n == 4 || n == 5)cout << -1 << endl;
else {
cout << "1 3" << endl; cout << "1 2" << endl; cout << "1 4" << endl;
for (int i = 5; i <= n; i++) {
cout << 3 << ' ' << i << endl;
}
}
for (int i = 1; i < n; i++)cout << i << ' ' << i + 1 << endl;
return 0;
}
