Machine learning 第8周编程作业 K-means and PCA

1.findClosestCentroids

 

function idx = findClosestCentroids(X, centroids)
%FINDCLOSESTCENTROIDS computes the centroid memberships for every example
%   idx = FINDCLOSESTCENTROIDS (X, centroids) returns the closest centroids
%   in idx for a dataset X where each row is a single example. idx = m x 1 
%   vector of centroid assignments (i.e. each entry in range [1..K])
%

% Set K
K = size(centroids, 1);

% You need to return the following variables correctly.
idx = zeros(size(X,1), 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Go over every example, find its closest centroid, and store
%               the index inside idx at the appropriate location.
%               Concretely, idx(i) should contain the index of the centroid
%               closest to example i. Hence, it should be a value in the 
%               range 1..K
%
% Note: You can use a for-loop over the examples to compute this.
%

for i=1:size(X,1),
  for j=1:K,
    dis(j)=sum( (centroids(j,:)-X(i,:)).^2, 2 );
  endfor
  [t,idx(i)]=min(dis);
endfor





% =============================================================

end

　　

 

2.computerCentroids

 

function centroids = computeCentroids(X, idx, K)
%COMPUTECENTROIDS returns the new centroids by computing the means of the 
%data points assigned to each centroid.
%   centroids = COMPUTECENTROIDS(X, idx, K) returns the new centroids by 
%   computing the means of the data points assigned to each centroid. It is
%   given a dataset X where each row is a single data point, a vector
%   idx of centroid assignments (i.e. each entry in range [1..K]) for each
%   example, and K, the number of centroids. You should return a matrix
%   centroids, where each row of centroids is the mean of the data points
%   assigned to it.
%

% Useful variables
[m n] = size(X);

% You need to return the following variables correctly.
centroids = zeros(K, n);


% ====================== YOUR CODE HERE ======================
% Instructions: Go over every centroid and compute mean of all points that
%               belong to it. Concretely, the row vector centroids(i, :)
%               should contain the mean of the data points assigned to
%               centroid i.
%
% Note: You can use a for-loop over the centroids to compute this.
%



for i=1:K,
  ALL=0;
  cnt=sum(idx==i);
  temp=find(idx==i);
  for j=1:numel(temp),
    ALL=ALL+X(temp(j),:);
  endfor
  centroids(i,:)=ALL/cnt;
endfor




% =============================================================


end

　　

3.pca

 

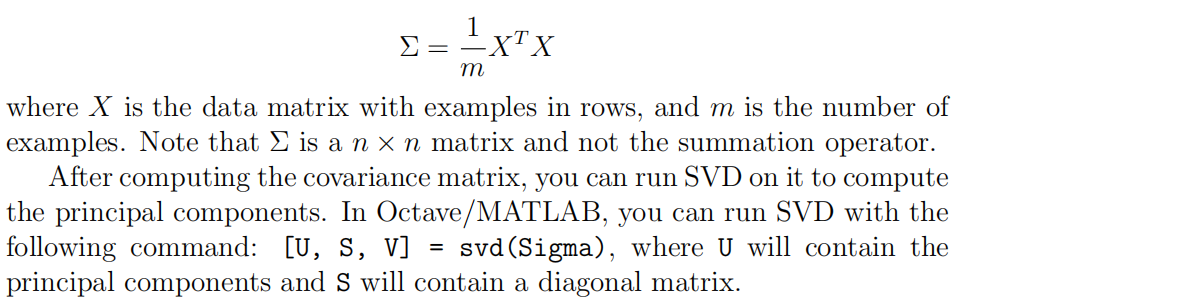
function [U, S] = pca(X)
%PCA Run principal component analysis on the dataset X
%   [U, S, X] = pca(X) computes eigenvectors of the covariance matrix of X
%   Returns the eigenvectors U, the eigenvalues (on diagonal) in S
%

% Useful values
[m, n] = size(X);

% You need to return the following variables correctly.
U = zeros(n);
S = zeros(n);

% ====================== YOUR CODE HERE ======================
% Instructions: You should first compute the covariance matrix. Then, you
%               should use the "svd" function to compute the eigenvectors
%               and eigenvalues of the covariance matrix. 
%
% Note: When computing the covariance matrix, remember to divide by m (the
%       number of examples).
%


Sigma=(X'*X)./m;
[U,S,V]=svd(Sigma);




% =========================================================================

end

　　

4.projectData

function Z = projectData(X, U, K)
%PROJECTDATA Computes the reduced data representation when projecting only 
%on to the top k eigenvectors
%   Z = projectData(X, U, K) computes the projection of 
%   the normalized inputs X into the reduced dimensional space spanned by
%   the first K columns of U. It returns the projected examples in Z.
%

% You need to return the following variables correctly.
Z = zeros(size(X, 1), K);

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the projection of the data using only the top K 
%               eigenvectors in U (first K columns). 
%               For the i-th example X(i,:), the projection on to the k-th 
%               eigenvector is given as follows:
%                    x = X(i, :)';
%                    projection_k = x' * U(:, k);
%

U_reduce=U(:,1:K);
Z=X*U_reduce;


% =============================================================

end

　　

 

5.recoverData

function X_rec = recoverData(Z, U, K)
%RECOVERDATA Recovers an approximation of the original data when using the 
%projected data
%   X_rec = RECOVERDATA(Z, U, K) recovers an approximation the 
%   original data that has been reduced to K dimensions. It returns the
%   approximate reconstruction in X_rec.
%

% You need to return the following variables correctly.
X_rec = zeros(size(Z, 1), size(U, 1));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the approximation of the data by projecting back
%               onto the original space using the top K eigenvectors in U.
%
%               For the i-th example Z(i,:), the (approximate)
%               recovered data for dimension j is given as follows:
%                    v = Z(i, :)';
%                    recovered_j = v' * U(j, 1:K)';
%
%               Notice that U(j, 1:K) is a row vector.
%               
X_rec=Z*U(:,1:K)';


% =============================================================

end