Machine learning吴恩达第三周 Logistic Regression

1. Sigmoid function

function g = sigmoid(z)
%SIGMOID Compute sigmoid function
%   g = SIGMOID(z) computes the sigmoid of z.

% You need to return the following variables correctly 
g = zeros(size(z));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the sigmoid of each value of z (z can be a matrix,
%               vector or scalar).

g=1./(1+exp(-z));



% =============================================================

end

 

 

2. Logistic Regression Cost &  Logistic Regression Gradient

 

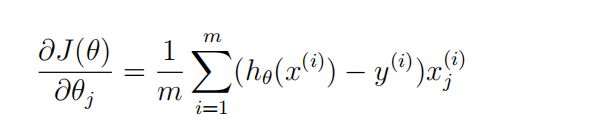
首先可以将h(x)表示出来----sigmoid函数

然后对于gredient(j)来说，

可以现在草稿纸上把矩阵画出来，然后观察，用向量来解决；

function [J, grad] = costFunction(theta, X, y)
%COSTFUNCTION Compute cost and gradient for logistic regression
%   J = COSTFUNCTION(theta, X, y) computes the cost of using theta as the
%   parameter for logistic regression and the gradient of the cost
%   w.r.t. to the parameters.

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta
%
% Note: grad should have the same dimensions as theta
%
h=sigmoid(X*theta);

for i=1:m,
  J=J+1/m*(-y(i)*log(h(i))-(1-y(i))*log(1-h(i)));
endfor

grad=1/m*X'*(h.-y);






% =============================================================

end

 

3. Predict

function p = predict(theta, X)
%PREDICT Predict whether the label is 0 or 1 using learned logistic 
%regression parameters theta
%   p = PREDICT(theta, X) computes the predictions for X using a 
%   threshold at 0.5 (i.e., if sigmoid(theta'*x) >= 0.5, predict 1)

m = size(X, 1); % Number of training examples

% You need to return the following variables correctly
p = zeros(m, 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned logistic regression parameters. 
%               You should set p to a vector of 0's and 1's
%


p=sigmoid(X*theta);
for i=1:m
  if(p(i)>=0.5)p(i)=1;
else p(i)=0;
  end 
endfor




% =========================================================================


end

 4.Regularized Logistic Regression Cost & Regularized Logistic Regression Gradient

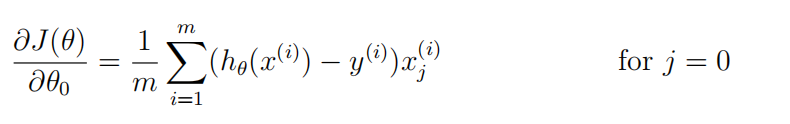
要注意的是：

Octave中，下标是从1开始的；

其次：

对于gradient(j)而言；

我们可以用X(:,j)的方式获取第j列的所有元素；

function [J, grad] = costFunctionReg(theta, X, y, lambda)
%COSTFUNCTIONREG Compute cost and gradient for logistic regression with regularization
%   J = COSTFUNCTIONREG(theta, X, y, lambda) computes the cost of using
%   theta as the parameter for regularized logistic regression and the
%   gradient of the cost w.r.t. to the parameters. 

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta

h=sigmoid(X*theta);

for i=1:m
  J=J+1/m*(-y(i)*log(h(i))-(1-y(i))*log(1-h(i)));
endfor

for i=2:length(theta)
  J=J+lambda/(2*m)*theta(i)^2;
endfor

grad(1)=1/m*(h-y)'*X(:,1);
for i=2:length(theta)
  grad(i)=1/m*(h-y)'*X(:,i)+lambda/m*theta(i);
endfor

% =============================================================

end