[NOI2010]能量采集 BZOJ2005 数学(反演)&&欧拉函数,分块除法
题目描述
栋栋有一块长方形的地,他在地上种了一种能量植物,这种植物可以采集太阳光的能量。在这些植物采集能量后,栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。
栋栋的植物种得非常整齐,一共有n列,每列有m棵,植物的横竖间距都一样,因此对于每一棵植物,栋栋可以用一个坐标(x, y)来表示,其中x的范围是1至n,表示是在第x列,y的范围是1至m,表示是在第x列的第y棵。
由于能量汇集机器较大,不便移动,栋栋将它放在了一个角上,坐标正好是(0, 0)。
能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有k棵植物,则能 量的损失为2k + 1。例如,当能量汇集机器收集坐标为(2, 4)的植物时,由于连接线段上存在一棵植物(1, 2),会产生3的能量损失。注意,如果一棵植物与能量汇集机器连接的线段上没有植物,则能量损失为1。现在要计算总的能量损失。
下面给出了一个能量采集的例子,其中n = 5,m = 4,一共有20棵植物,在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。
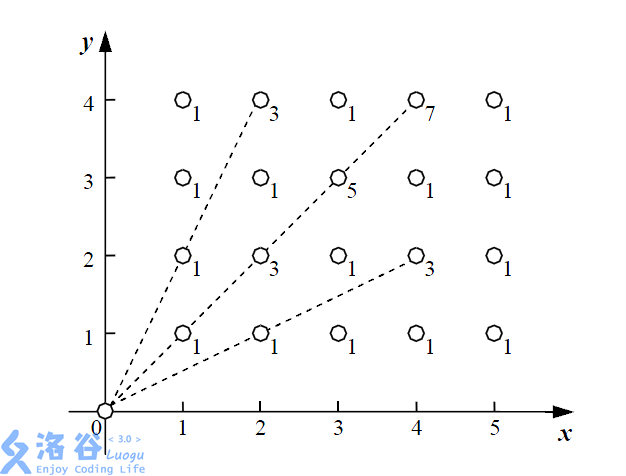
在这个例子中,总共产生了36的能量损失。
输入输出格式
输入格式:仅包含一行,为两个整数n和m。
输出格式:仅包含一个整数,表示总共产生的能量损失。
输入输出样例
说明
对于10%的数据:1 ≤ n, m ≤ 10;
对于50%的数据:1 ≤ n, m ≤ 100;
对于80%的数据:1 ≤ n, m ≤ 1000;
对于90%的数据:1 ≤ n, m ≤ 10,000;
对于100%的数据:1 ≤ n, m ≤ 100,000。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<time.h>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize(2)
using namespace std;
#define maxn 200005
#define inf 0x7fffffff
//#define INF 1e18
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
#define mclr(x,a) memset((x),a,sizeof(x))
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-5
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline int rd() {
int x = 0;
char c = getchar();
bool f = false;
while (!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
while (isdigit(c)) {
x = (x << 1) + (x << 3) + (c ^ 48);
c = getchar();
}
return f ? -x : x;
}
ll gcd(ll a, ll b) {
return b == 0 ? a : gcd(b, a%b);
}
int sqr(int x) { return x * x; }
/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
if (!b) {
x = 1; y = 0; return a;
}
ans = exgcd(b, a%b, x, y);
ll t = x; x = y; y = t - a / b * y;
return ans;
}
*/
int tot;
int vis[maxn];
ll phi[maxn], sum[maxn], p[maxn], n, m;
void init() {
phi[1] = 1;
for (int i = 2; i <= maxn; i++) {
if (!vis[i]) {
p[++tot] = i; phi[i] = i - 1;
}
for (int j = 1; j <= tot && i*p[j] <= maxn; j++) {
vis[i*p[j]] = 1;
phi[i*p[j]] = phi[i] * phi[p[j]];
if (i%p[j] == 0) {
phi[i*p[j]] = phi[i] * p[j]; break;
}
}
}
}
int main()
{
// ios::sync_with_stdio(0);
rdllt(n); rdllt(m);
init(); ll ans = 0;
// cout << phi[10] << ' ' << phi[5] << endl;
for (int i = 1; i <= maxn; i++)sum[i] = sum[i - 1] + phi[i];
for (int l = 1, r; l <= min(n, m); l = r + 1) {
r = min(n / (n / l), m / (m / l));
ans += 1ll * (sum[r] - sum[l - 1])*(n / l)*(m / l);
}
cout << (ll)(2ll * ans - n * m) << endl;
return 0;
}
EPFL - Fighting


