[BJWC2008]雷涛的小猫 dp
题目背景
原最大整数参见P1012
题目描述
雷涛同学非常的有爱心,在他的宿舍里,养着一只因为受伤被救助的小猫(当然,这样的行为是违反学生宿舍管理条例的)。在他的照顾下,小猫很快恢复了健康,并且愈发的活泼可爱了。
可是有一天,雷涛下课回到寝室,却发现小猫不见了!经过一番寻找,才发现她正趴在阳台上对窗外的柿子树发呆…
在北京大学的校园里,有许多柿子树,在雷涛所在的宿舍楼前,就有N棵。并且这N棵柿子树每棵的高度都是H。冬天的寒冷渐渐笼罩了大地,树上的叶子渐渐掉光了,只剩下一个个黄澄澄的柿子,看着非常喜人。而雷涛的小猫恰好非常的爱吃柿子,看着窗外树上的柿子,她十分眼馋,于是决定利用自己敏捷的跳跃能力跳到树上去吃柿子。
小猫可以从宿舍的阳台上跳到窗外任意一棵柿子树的树顶。之后,她每次都可以在当前位置沿着当前所在的柿子树向下跳111单位距离。当然,小猫的能力远不止如此,她还可以在树之间跳跃。每次她都可以从当前这棵树跳到另外的任意一棵,在这个过程中,她的高度会下降Delta单位距离。每个时刻,只要她所在的位置有柿子,她就可以吃掉。整个“吃柿子行动”一直到小猫落到地面上为止。
雷涛调查了所有柿子树上柿子的生长情况。他很想知道,小猫从阳台出发,最多能吃到多少柿子?他知道写一个程序可以很容易的解决这个问题,但是他现在懒于写任何代码。于是,现在你的任务就是帮助雷涛写一个这样的程序。
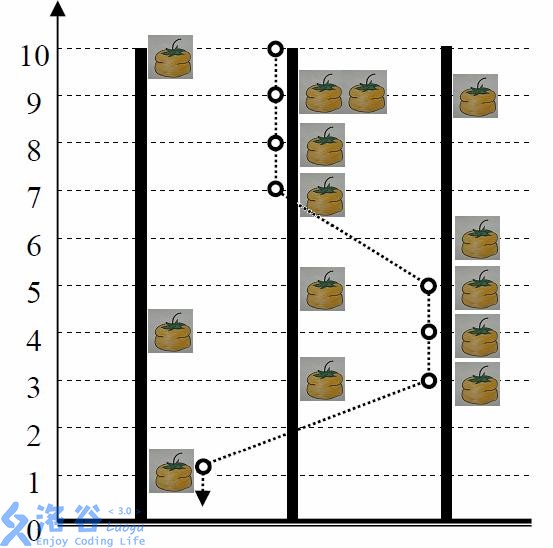
图为N=3,H=10,Delta=2N=3, H=10, Delta=2N=3,H=10,Delta=2的一个例子。小猫按照图示路线进行跳跃,可以吃到最多的888个柿子
输入输出格式
输入格式:第一行有三个以空格分隔的整数,分别代表N,H,DeltaN,H,DeltaN,H,Delta
接下来的NNN行,每行第一个整数为NiN_iNi,代表第i棵树上的柿子数量。
接下来是NiN_iNi个整数,每个整数Tij代表第i棵柿子树的TijT_{ij}Tij高度上长有一个柿子。
输出格式:一个整数,即小猫最多吃到的柿子数。
输入输出样例
说明
1≤N,H≤20001 ≤ N, H ≤ 20001≤N,H≤2000
0≤Ni≤50000 ≤ N_i ≤ 50000≤Ni≤5000
1≤Delta≤N,1≤Tij≤H1 ≤ Delta ≤ N,1 ≤ T_{ij} ≤ H1≤Delta≤N,1≤Tij≤H
输入文件大小不大于40960KB40960KB40960KB
来源 Excalibur, 2008
不太明白为什么luogu把这个标签放置为 “贪心”里面;
当然应该是 dp ;
转移方程: dp[ i ][ j ]=max( dp[ i ][ j+1 ]+maxx[ j+dlt ] )+ num[ i ][ j ];
maxx [ j ]=max( maxx[ j ],dp[ i ][ j ] );
其中 dpi,j 表示在第 i 棵树,高度为 j 时的最优值;
maxxi 表示 高度为 i 时的最优解;
然后 dp 就完成了;
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize(2)
using namespace std;
#define maxn 200005
#define inf 0x7fffffff
//#define INF 1e18
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline ll rd() {
ll x = 0;
char c = getchar();
bool f = false;
while (!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
while (isdigit(c)) {
x = (x << 1) + (x << 3) + (c ^ 48);
c = getchar();
}
return f ? -x : x;
}
ll gcd(ll a, ll b) {
return b == 0 ? a : gcd(b, a%b);
}
int sqr(int x) { return x * x; }
/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
if (!b) {
x = 1; y = 0; return a;
}
ans = exgcd(b, a%b, x, y);
ll t = x; x = y; y = t - a / b * y;
return ans;
}
*/
int N, H, dlt;
int num[3000][5010];
int dp[3000][5001];
int maxx[maxn];
int main() {
//ios::sync_with_stdio(0);
rdint(N); rdint(H); rdint(dlt);
for (int i = 1; i <= N; i++) {
int tmp; rdint(tmp);
for (int j = 1; j <= tmp; j++) {
int tmpy; rdint(tmpy);
num[i][tmpy]++;
}
}
for (int i = H; i >= 1; i--) {
for (int j = 1; j <= N; j++) {
dp[j][i] = max(dp[j][i + 1], maxx[i + dlt]) + num[j][i];
maxx[i] = max(maxx[i], dp[j][i]);
}
}
printf("%d\n", maxx[1]);
return 0;
}


