CF912D Fishes 期望
题意翻译
Description
有一个长为nnn ,宽为mmm 的鱼缸,还有一个边长为rrr 的正方形渔网。你可以往鱼缸里放kkk 条鱼,问用渔网随机在浴缸里捞鱼的最大期望是多少。不懂什么是期望的自己去百度
Input
一行4个正整数代表n,m,r,kn, m, r, kn,m,r,k
Output
输出一个实数,表示最大期望
感谢@xunzhen 提供的翻译
题目描述
While Grisha was celebrating New Year with Ded Moroz, Misha gifted Sasha a small rectangular pond of size n×m n×m n×m , divided into cells of size 1×1 1×1 1×1 , inhabited by tiny evil fishes (no more than one fish per cell, otherwise they'll strife!).
The gift bundle also includes a square scoop of size r×r r×r r×r , designed for fishing. If the lower-left corner of the scoop-net is located at cell (x,y) (x,y) (x,y) , all fishes inside the square (x,y)...(x+r−1,y+r−1) (x,y)...(x+r-1,y+r-1) (x,y)...(x+r−1,y+r−1) get caught. Note that the scoop-net should lie completely inside the pond when used.
Unfortunately, Sasha is not that skilled in fishing and hence throws the scoop randomly. In order to not frustrate Sasha, Misha decided to release k k k fishes into the empty pond in such a way that the expected value of the number of caught fishes is as high as possible. Help Misha! In other words, put k k k fishes in the pond into distinct cells in such a way that when the scoop-net is placed into a random position among (n−r+1)⋅(m−r+1) (n-r+1)·(m-r+1) (n−r+1)⋅(m−r+1) possible positions, the average number of caught fishes is as high as possible.
输入输出格式
输入格式:The only line contains four integers n,m,r,k n,m,r,k n,m,r,k ( 1<=n,m<=105 1<=n,m<=10^{5} 1<=n,m<=105 , 1<=r<=min(n,m) 1<=r<=min(n,m) 1<=r<=min(n,m) , 1<=k<=min(n⋅m,105) 1<=k<=min(n·m,10^{5}) 1<=k<=min(n⋅m,105) ).
输出格式:Print a single number — the maximum possible expected number of caught fishes.
You answer is considered correct, is its absolute or relative error does not exceed 10−9 10^{-9} 10−9 . Namely, let your answer be a a a , and the jury's answer be b b b . Your answer is considered correct, if 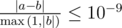 .
.
输入输出样例
说明
In the first example you can put the fishes in cells (2,1) (2,1) (2,1) , (2,2) (2,2) (2,2) , (2,3) (2,3) (2,3) . In this case, for any of four possible positions of the scoop-net (highlighted with light green), the number of fishes inside is equal to two, and so is the expected value.
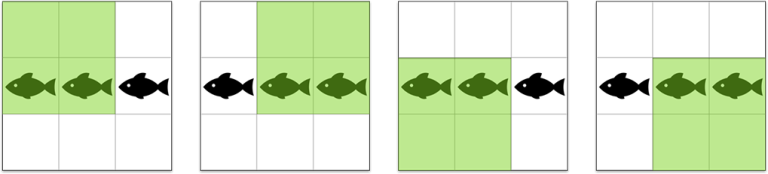
很容易想到的一种思路是在被正方形覆盖次数最多的地方放🐟;
那么我们要做的就是给定(x,y)坐标后,求出该位置被多少个矩形所覆盖即可;
接着从该位置向四周拓展----bfs;
当然用 priority-queue维护一下即可解决;
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize(2)
using namespace std;
#define maxn 300005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline ll rd() {
ll x = 0;
char c = getchar();
bool f = false;
while (!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
while (isdigit(c)) {
x = (x << 1) + (x << 3) + (c ^ 48);
c = getchar();
}
return f ? -x : x;
}
ll gcd(ll a, ll b) {
return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }
/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
if (!b) {
x = 1; y = 0; return a;
}
ans = exgcd(b, a%b, x, y);
ll t = x; x = y; y = t - a / b * y;
return ans;
}
*/
double ans = 0;
int n, m, k, r;
int dx[] = { 0,1,0,-1 };
int dy[] = { 1,0,-1,0 };
struct node {
int x, y;
ll sum;
friend bool operator <(node a, node b) {
return a.sum < b.sum;
}
};
priority_queue<node>q;
map<pii, int>fg;
bool judge(int x, int y) {
if (x >= 1 && x <= n && y >= 1 && y <= m&&fg[make_pair(x,y)]==0)return true;
if (fg[make_pair(x, y)])return 0;
return 0;
}
ll getsum(int x, int y) {
ll X = min(n, x + r - 1) - max(r, x) + 1;
ll Y = min(m, y + r - 1) - max(y, r) + 1;
return X * Y;
}
int main()
{
//ios::sync_with_stdio(0);
rdint(n); rdint(m); rdint(r); rdint(k);
fg[make_pair((n+1)/2, (m+1)/2)] = 1;
q.push(node{ (n + 1) / 2,(m + 1) / 2,getsum((n + 1) / 2,(m + 1) / 2) });
while (k--) {
node tmp = q.top(); q.pop();
int x = tmp.x, y = tmp.y;
ans += 1.0*tmp.sum / (n - r + 1) / (m - r + 1);
for (int i = 0; i < 4; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (judge(nx, ny)) {
fg[make_pair(nx, ny)] = 1;
q.push(node { nx, ny, getsum(nx, ny) });
}
}
}
printf("%.10lf\n", 1.0*ans);
return 0;
}


