《剑指offer》刷题记录

day1 / 9

剑指 Offer 34. 二叉树中和为某一值的路径

输入：

[-2,null,-3] -5

输出：

[]

预期结果：

[[-2,-3]]
if(l < 0 || node == nullptr)return;
改成
if(node == nullptr)return;
temppath.push_back(node->val);
l -= node->val;
if(!node->left && !node->right && !l){
  ans.push_back(temppath);
}
紧贴题意：叶子节点 & 为0

🤔 如果写成
if(!node->left && !node->right){
 if(l==0){
     ans.push_back(temppath);
 }
 return;
}
会快很多

剑指 Offer 03. 数组中重复的数字

数组中重复1次的元素

❗异或运算和顺序无关，甚至可以并行实现

数组中2个重复1次的元素

干货！史上最强位运算面试题大总结！ - 九章算法的文章 - 知乎

位运算解决“一个数组中，只有一个数字出现n次，其他数字出现k次”问题

给你1-1000个连续自然数，然后从中随机去掉两个，再打乱顺序，要求只遍历一次，求出被去掉的两个。

———[x]——[y]———(1)

————————(2)

然后(1)(2)合并，采用数组中两个重复两次的元素的思路即可

详细的分析

元素重复3次的数组中查找重复1次的元素

元素重复k次的数组中查找重复1次的元素

剑指 Offer 07. 重建二叉树

剑指 Offer 05. 替换空格

主动和面试官询问内存要求
对内存覆盖要有敏锐的感觉
- 数组的数据移动需要时间

剑指 Offer 08 在二叉树中找到一个节点的后继节点

对中序遍历的理解

node* s;
if(q->r != null){	
    // 存在右子树
    s = q->r;
    while(s->l)s = s->l;
}else{
    // 没有右子树，下一个节点是“将当前节点包含于其左子树中的最低祖先”
    s = q->parent;
    // 需要将根节点的祖先设置为一个特殊值
    while(s->parent && s->parent->right == s)s = s->parent;
    s = s->parent; // 如果是根节点，则返回的是特殊值
}

剑指 Offer 09. 用两个栈实现队列

栈混洗

PTA 彩虹瓶

// https://pintia.cn/problem-sets/994805046380707840/problems/1111914599412858889
// 彩虹瓶 栈混洗
#include<stdio.h>
#include<stack>
using namespace std;
const int N = 1000 + 100;
int n,m,nn;
int a[N];
stack<int > s;
int main(){
	scanf("%d %d %d",&n,&m,&nn);
	while(nn--){
		for(int i =0;i<n;i++){
			scanf("%d",&a[i]);
		}
		int b = 1;
		int cura = 0;
		bool r = true;
		while(b<=n){
			if(a[cura] == b){
				cura++;b++; 
			}else{
				if(!s.empty()&&s.top() == b){
					// 从s 中弹出 
					b++;s.pop();
				}else if(s.empty() || !s.empty() && s.top() != b){
					if(cura>=n){
						r = false; break;
					}
					s.push(a[cura++]);
					if(s.size()>m){
						r = false;break;
					}
				}
			}
		}
		if(r)printf("YES\n");
		else printf("NO\n");
		while(!s.empty())s.pop();
	}
}

剑指 Offer 10- II. 青蛙跳台阶问题

记忆化搜索

⭐剑指 Offer 68 - II. 二叉树的最近公共祖先

这道题在力扣里面是简单 / 中等题，但是仍然可以学到很多东西

关键是要积极思考

注意到，这里二叉树的最近公共祖先有一个很好的性质——唯一性

dfs的在树当中从根节点开始不会两次打开同一个节点，时间复杂度可以比较好地保证，空间复杂度也可以做到 O(logn)（平均）~O(n)之间

但是问题在于，dfs的单次遍历需要返回一个有助于上层决策的值，或者修改某全局变量

全局找到答案时，也就时找到了唯一必然存在的一个答案，可以想象成找到了一个永远无法被打败的擂主

这个题目当中，每一个节点可以向上返回四个值 lp,rp,lq,rq

（当然，在java当中这样的返回看上去有点不太方便，在C当中使用指针能比较方便地实现）

他们满足
lp && rp == 0;
lq && rq == 0;

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if(root == null || root == p || root == q)return root;
    TreeNode left = lowestCommonAncestor(root.left,p,q);
    TreeNode right = lowestCommonAncestor(root.right,p,q);
    if(left == null)return right;
    if(right == null)return left;
    return root;
}

😆 这段代码太漂亮了！

也可以这样实现

TreeNode ans;
boolean dfs(TreeNode root, TreeNode p, TreeNode q){
    if(root == null) return false;
    boolean ll = dfs(root.left,p,q);
    boolean rr = dfs(root.right,p,q);
    boolean self = root== p || root== q;
    if(ans == null && (ll&rr)|| self && (ll || rr)){
        ans = root;
    }
    return ll || rr || self;
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    ans = null;
    dfs(root,p,q);
    return ans;
}

扩展阅读

day2 / to 21

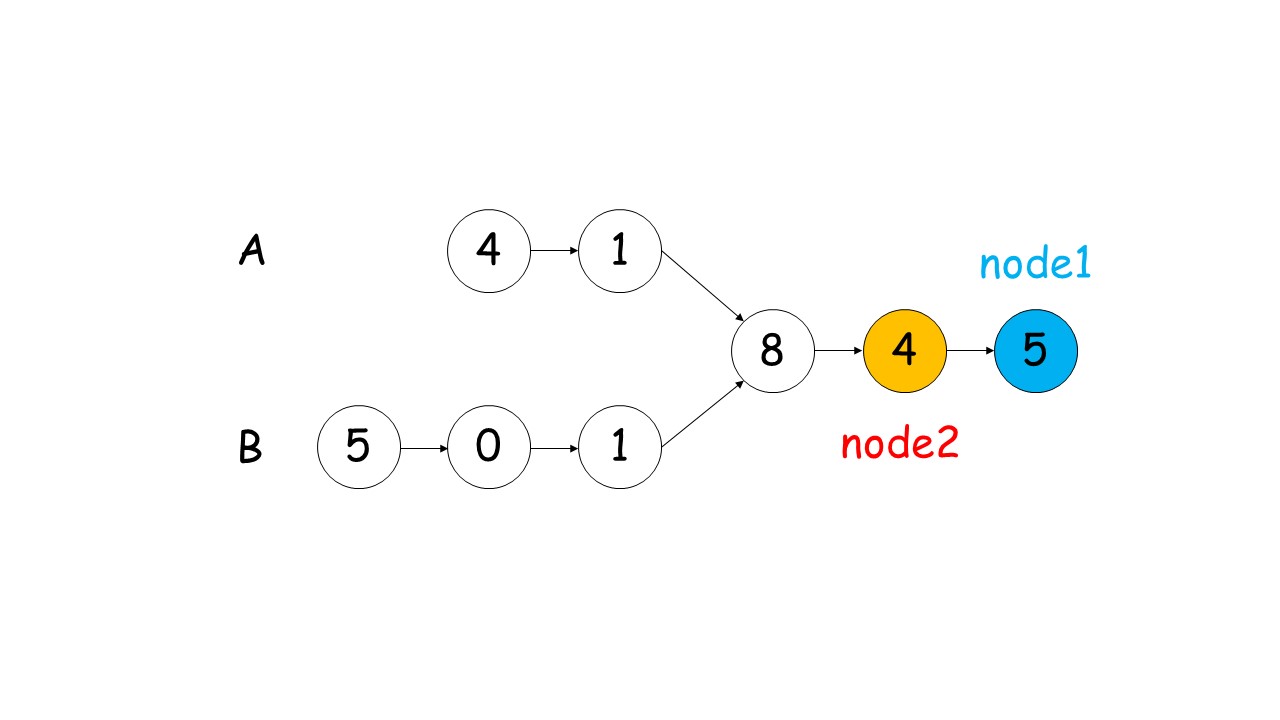
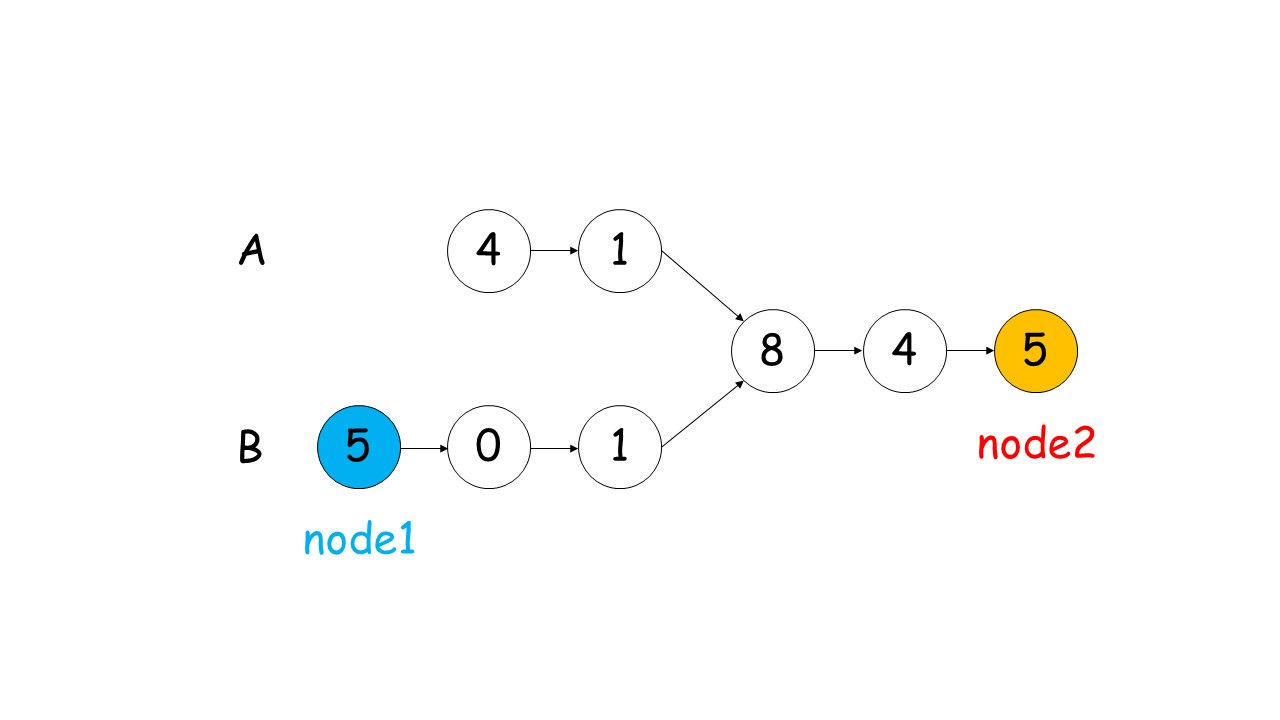
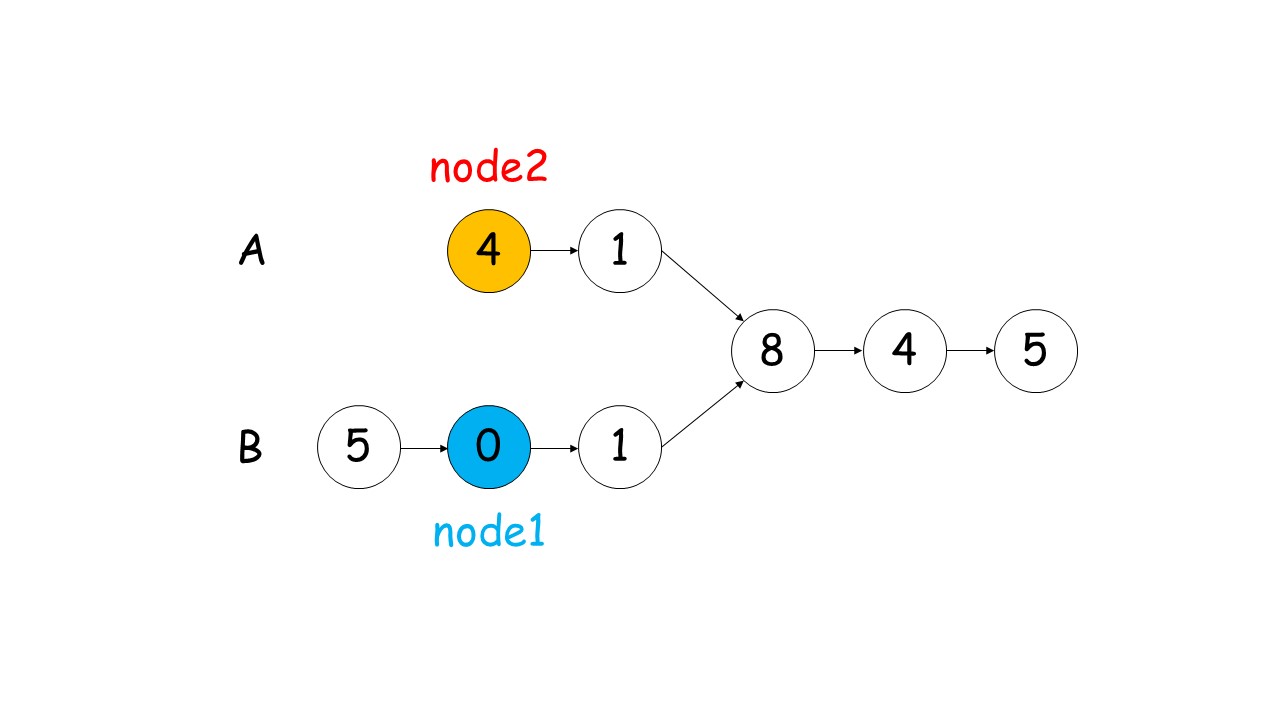
剑指 Offer 52. 两个链表的第一个公共节点

双指针是比较巧妙的方法

但是有更直观的方法

辅助栈实现链表倒序遍历（这也是很基础却很重要的一种思想，类似于拓扑排序实现bfs）
双指针的等价做法

设定两个指针分别指向两个链表头部，一起向前走直到其中一个到达末端，另一个与末端距离则是两链表的长度差。再通过长链表指针先走的方式消除长度差，最终两链表即可同时走到相交点。

作者：jyd
链接：https://leetcode-cn.com/problems/intersection-of-two-linked-lists/solution/intersection-of-two-linked-lists-shuang-zhi-zhen-l/

剑指 Offer 11. 旋转数组的最小数字

剑指 Offer 12. 矩阵中的路径

int n;
int m;
boolean[][] vis;
boolean dfs(char[][] board,int i, int j,String word,int cur){
    if(i<0||j<0||i>=n||j>=m )return false;
    if(board[i][j] != word.charAt(cur) || vis[i][j])return false;
    vis[i][j] = true;
    if(cur == word.length()-1)return true;
    return dfs(board,i+1,j,word,cur+1)||dfs(board,i-1,j,word,cur+1)||dfs(board,i,j+1,word,cur+1)||dfs(board,i,j-1,word,cur+1);
}
public boolean exist(char[][] board, String word) {
    n = board.length;
    if(n == 0)return false;
    m = board[0].length;
    for(int i = 0;i<n;i++){
        for(int j = 0;j<m;j++){
            if(board[i][j] == word.charAt(0)){
                vis = new boolean[n+100][m+100];
                if(dfs(board,i,j,word,0))return true;
            }
        }
    }
    return false;
}

上面有一个 vis没有复原的错误

应该是

vis[i][j] = true;
boolean r = dfs(board,i+1,j,word,cur+1)||dfs(board,i-1,j,word,cur+1)||dfs(board,i,j+1,word,cur+1)||dfs(board,i,j-1,word,cur+1);
vis[i][j] = false;

剑指 Offer 14- I. 剪绳子

官方题解

剑指 Offer 15. 二进制中1的个数

int tot = 0;
while(n!=0){
    tot++;
    n&=(n-1);
}

❗移位运算有算术移位和逻辑移位之分

while(n)if(n & 1)tot ++,n >>= 1;的方法可能会涉及符号位1移入的问题。

可以考虑进行无符号数强转；uint32_t nn = (uint32_t)n;

如果采用 n&(1<<i)的判断方法则可以避免涉及符号问题

剑指 Offer 16. 数值的整数次方

at line 3, Solution.myPow

最后执行的输入：

1.00000 -2147483648

反转之后溢出……，可以抽出一个因子来

if(n<0)return (1/x)*myPow(x,-(n+1));

剑指 Offer 17. 打印从1到最大的n位数

对大数问题的敏感性
大数高精度加法

剑指 Offer 18. 删除链表的节点

`O(1)`平均复杂度完成链表节点删除

cur.next = cur.next.next;
cur.val = cur.next.val;

```
if(cur == head){
	head = cur.next;
}
```

if(cur.next == null){
	// O(n 遍历找到前序节点)
}

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

public int[] exchange(int[] nums) {
    int n = nums.length;
    int i1 = 0;
    int i2 = n-1;
    while(i1<i2){
        while(i1<n && nums[i1]%2==1)i1++;
        if(i1 == n)return nums;
        if(nums[i1]%2 == 0){
            while(i2>0 && nums[i2]%2 == 0 && i2>i1){
                i2--;
            }
            int temp = nums[i2];nums[i2] = nums[i1];nums[i1] = temp;
            i1++;i2--;
        }
    }
    return nums;
}

可以换成这样简洁的代码

while(i<j){
    while(i<j && nums[i]%2==1)i++;
    while(i<j && nums[j]%2==0)j--;
    temp = nums[i];nums[i] = nums[j];nums[j] = temp;
}

:happy:这其实也是快排当中哨兵的思想，哨兵单向移动，本身就可以做界限

快排模板

void qsort(int[]arr,int l,int r){
    if(l>=r)return;
    int i = l + 1,j = r,mid = (l+r)/2;
    // Sherwood随机化
	swap(a[l],a[mid]);
    while(i<j){
        while(i<j&&a[j]>=p)j--;
        while(i<j&&a[i]<=p)i++;
        swap(a[i],a[j]);
    }
    swap(a[l],a[i]);
    qsort(a,l,mid-1);
    qsort(a,mid+1,r);
}

为什么不可以随机化为 i = l+1
- 这样就违背了i先走的原则！
为什么最后保证 a[l]还可以和轴点交换？
- 因为如果 a[l]被改变，只有一种情况：a[l]就是最小元素，因为如果不是最小元素，i一定可以跳过l

day3

鲁棒性

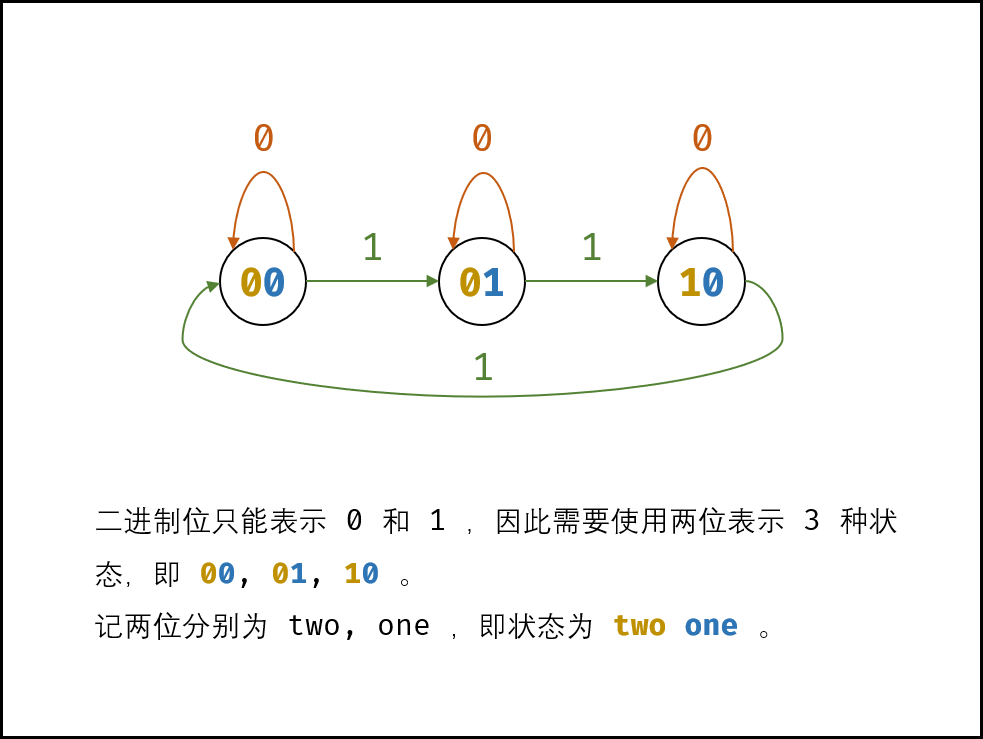
⭐剑指 Offer 20. 表示数值的字符串

编写DFA的规范是什么，DFA的函数应该返回一个什么值？

这个概念本身是不太规范的。DFA是一个广泛使用的概念，而在编译当中，应该说是语法分析更为恰当。

If the next input character is not one that can begin a comparison operator, then a function fail() is called. What fail() does depends on the global error-recovery strategy of the lexical analyzer.

——龙书

🤔 有没有优雅一点的方法做越界判断

class Solution {
    int cur;
    int n;
    char[] s;
    boolean isd(char c){
        return (c<='9' && c>='0');
    }
    boolean readUnsigned(){
        boolean r = false;
        while(cur < n && isd(s[cur])){
            r= true;
            cur++;
        }
        return r;
    }
    boolean readInt(){
        boolean r = false;
        if(cur < n && (s[cur] == '+' || s[cur] == '-'))cur++;
        return readUnsigned();
    }
    public boolean isNumber(String _s) {
        s  = _s.toLowerCase().trim().toCharArray();
        n = s.length;
        boolean r = false;
        r = readInt();
        if(cur<n && s[cur] == '.'){
            cur ++; // 注意单独取一个字符需要主动预读
            // 小数
            r |= readUnsigned();
            System.out.println(r);
            System.out.println(cur);
        }
        if(cur< n && s[cur] == 'e'){
            // 与的原因是，指数必须要有合法底数才行
            cur ++;
            // 这里的指数只能是整形
            r &= readInt();
        }
        return r && cur == n;
    }
}

⭐剑指 Offer 22. 链表中倒数第k个节点

这里的鲁棒性判断非常重要！

Node* getkthFromEnd(Node * head, unsigned int k)

head = null
k <= 0 或者 len < k
在代码当中会有 k–，如果 k = 0(uint32_t)，那么k 会变成一个 2^32-1 = 0xFFFFFFFF

剑指 Offer 23. 寻找链表中的环

修改列表本身的结构
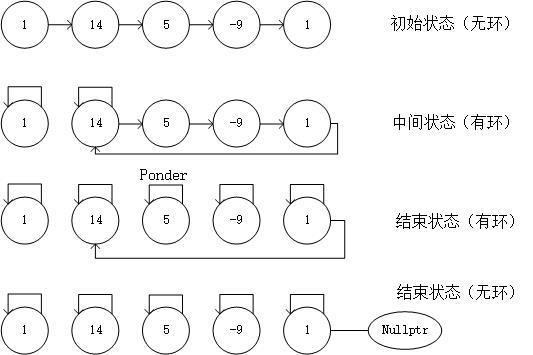
快慢指针

Node fast = head;
Node slow = head;
do{
    if(fast == null || fast.next == null)return null;
    slow = slow.next;
    fast = fast.next.next;
}while(fast != slow);
// 找到入口节点
Node cur = head;
while(cur != slow)cur = cur.next,slow = slow.next;
return slow;

剑指 Offer 24. 反转链表

head.next.next = head;这个表达很巧妙

public ListNode reverseList(ListNode head) {
    if(head == null || head.next == null)return head;
    ListNode tail = reverseList(head.next);
    head.next.next = head;
    head.next = null;
    return tail;
}

剑指 Offer 26. 树的子结构

public boolean isSubStructure(TreeNode A, TreeNode B) {
    if(A == null && B == null)return true;
    else if(A == null && B!=null || A!=null && B ==null)return false;
    if(A.val == B.val){
        return isSubStructure(A.left,B.left) && isSubStructure(A.right,B.right) || isSubStructure(A.left,B) || isSubStructure(A.right,B);
    }else{
        return isSubStructure(A.left,B) || isSubStructure(A.right,B);
    }
}

class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B, boolean fixed) {
        if(B == null)return true;
        else if(A == null && B!=null)return false;
        if(A.val == B.val){
            if(fixed) return isSubStructure(A.left,B.left,true) && isSubStructure(A.right,B.right,true);
            else return isSubStructure(A.left,B.left,true) && isSubStructure(A.right,B.right,true) || isSubStructure(A.left,B,false) || isSubStructure(A.right,B,false);
        }else{
            if(fixed)return false;
            return isSubStructure(A.left,B,false) || isSubStructure(A.right,B,false);
        }
    }
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        if(A!=null && B == null)return false;
        return isSubStructure(A, B,false);
    }
}

输入：

[-1,3,2,0] []

输出：

true

预期结果：

false

看看人家这美丽的代码 🌹

注意这种多函数递归的情况

class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        if (A == null || B == null) return false;
        return judge(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
    }

    private boolean judge(TreeNode A, TreeNode B) {
        return (A == null || B == null) ? (B == null) : (A.val == B.val) && judge(A.left, B.left) && judge(A.right, B.right);
    }
}

作者：ggeorge500
链接：https://leetcode-cn.com/problems/shu-de-zi-jie-gou-lcof/solution/java-san-xing-luo-ji-dai-ma-dfs-shuang-bai-tong-gu/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

剑指 Offer 27,28. 镜像，对称的二叉树

两种递归策略

自身递归 isSymmetric(root)
调用子函数 mir(root,root)

剑指 Offer 29. 顺时针打印矩阵

剑指 Offer 30. 包含min函数的栈

输入：

["MinStack","push","push","push","top","pop","getMin","pop","getMin","pop","push","top","getMin","push","top","getMin","pop","getMin"] [[],[2147483646],[2147483646],[2147483647],[],[],[],[],[],[],[2147483647],[],[],[-2147483648],[],[],[],[]]

输出：

[null,null,null,null,2147483647,null,1061109567,null,1061109567,null,null,2147483647,1061109567,null,-2147483648,-2147483648,null,1061109567]

预期结果：

[null,null,null,null,2147483647,null,2147483646,null,2147483646,null,null,2147483647,21]

✔️不要想当然！

直接设置一个成员变量貌似可行，但实际这个变量只能记录，但无法处理pop()带来的动态更新

直接的想法是：想象一个动态的场景，如果弹出一个元素，我需要立即更新全局最小值，如果全局最小值是自己，那么我需要立即找到次小值，如果不是，那么可以安全弹出。

class MinStack {
    int INF = 0x7FFFFFFF;
    ArrayList<Integer> a;
    ArrayList<Integer> min;
    ArrayList<Integer> secmin;
    int cur = -1;
    /** initialize your data structure here. */
    public MinStack() {
        a = new ArrayList<Integer>();
        min = new ArrayList<Integer>();
        secmin = new ArrayList<Integer>();
        a.add(INF);
        cur ++;
        secmin.add(cur);
        min.add(cur);
    }
    
    public void push(int x) {
        int i_min = min.get(cur);
        int i_secmin = secmin.get(cur);
        int _min = a.get(i_min);
        int _secmin = a.get(i_secmin);
        cur ++;
        if(x<=_min){
            min.add(cur);
            secmin.add(i_min);
        }else if(_min < x && x<= _secmin){
            min.add(i_min);
            secmin.add(cur);
        }else{
            min.add(i_min);
            secmin.add(i_secmin);
        }
        a.add(x);
    }
    
    public void pop() {
        if(cur <0)return;
        a.remove(cur);
        min.remove(cur);
        secmin.remove(cur);
        cur --;
    }
    
    public int top() {
        return a.get(cur);
    }
    
    public int getMin() {
        int ii = min.get(cur);
        return a.get(ii);
    }
}

😂但其实根本不用这么麻烦hhh

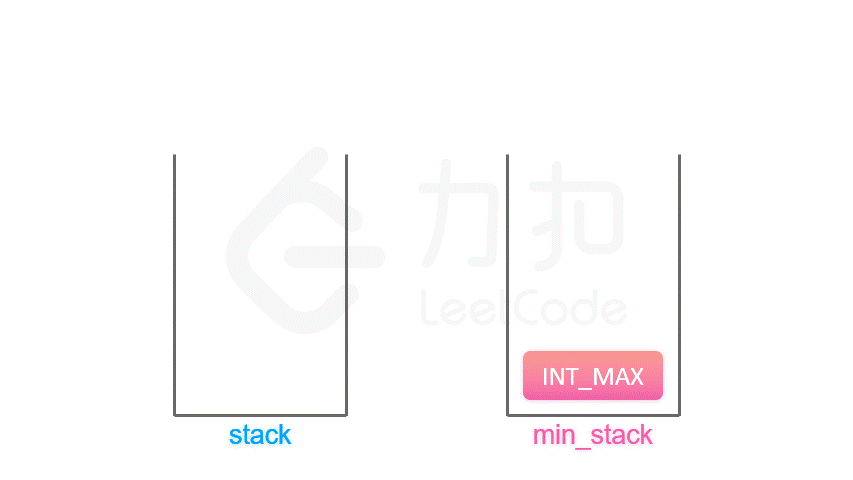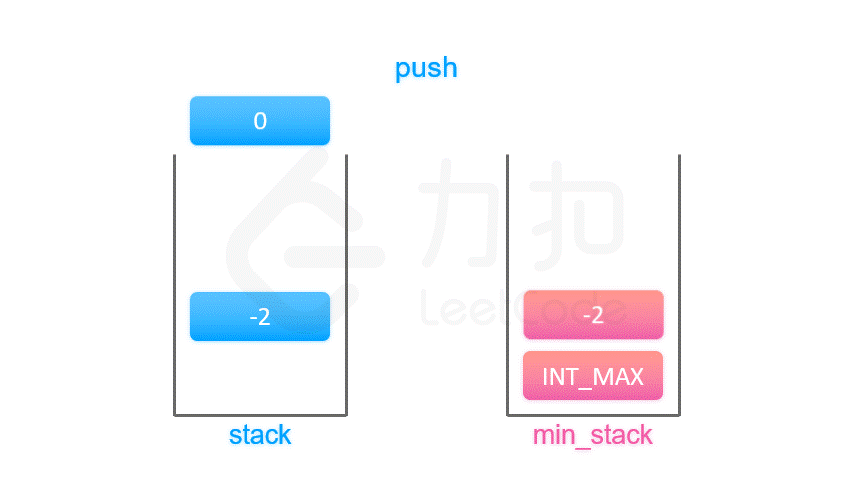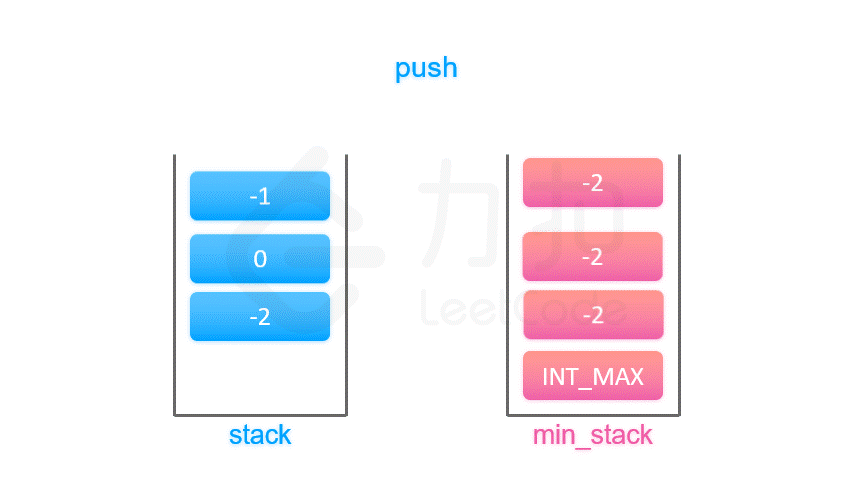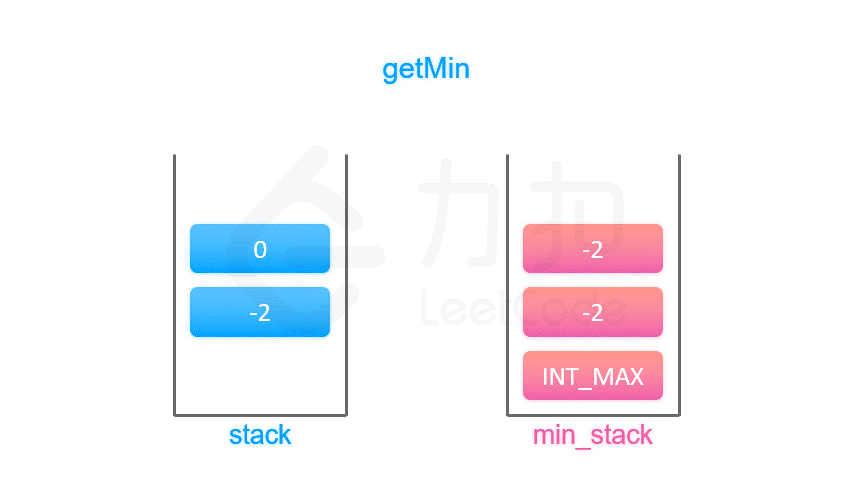
day4

剑指 Offer 31. 栈的压入、弹出序列

栈混洗

剑指 Offer 32 从上到下打印二叉树

直接层序遍历

分层层序遍历

可以用递归实现

List<List<Integer>> ans;
public List<List<Integer>> levelOrder(TreeNode root) {
    ans = new ArrayList<>();
    lev(1,root);
    return ans;
}
void lev(int level,TreeNode root){
    if(root == null)return;
    if(ans.size() < level)ans.add(new ArrayList<Integer>());
    ans.get(level -1).add(root.val);
    lev(level+1,root.left);
    lev(level+1,root.right);
}

分层倒序层序遍历

剑指 Offer 35. 复杂链表的复制

class Solution {
    void dup(Node head){
        Node cur = head;
        Node temp = cur;
        while(cur!=null){
            temp = cur.next;
            cur.next = new Node(0);
            cur.next.val = cur.val;
            cur.next.next = temp;
            cur = temp;
        }
    }
    void connect(Node head){
        Node oldnode = head;
        Node newnode = head;
        while(oldnode!=null){
            newnode = oldnode.next;
            newnode.random = oldnode.random == null ? null:oldnode.random.next;
            oldnode = newnode.next;
        }
    }
    Node split(Node oldhead){
        Node newhead = oldhead.next;
        Node oldnode = oldhead;
        Node newnode = oldhead.next;
        while(oldnode!=null){
            newnode = oldnode.next;
            oldnode.next = newnode.next;
            newnode.next = newnode.next == null? null:newnode.next.next;
            oldnode = oldnode.next;
        }
        return newhead;
    }
    public Node copyRandomList(Node head) {
        if(head == null)return null;
        dup(head);
        connect(head);
        return split(head);
    }
}

剑指 Offer 36. 二叉搜索树与双向链表

class Solution {
    public Node treeToDoublyList(Node root) {
        Node[] ret = getBid(root);
        Node ans = ret[0];
        if(ret[0]!=null){
            ret[0].left = ret[1];
            ret[1].right = ret[0];
        }
        return ans;
    }
    Node[] getBid(Node root){
        if(root == null) return new Node[]{null,null};
        Node[] ret = new Node[2];
        Node[] l = getBid(root.left);
        Node[] r = getBid(root.right);
        Node l1 = l[0];
        Node l2 = l[1];
        Node r1 = r[0];
        Node r2 = r[1];
        if(l2 == null){
            root.left = null;
            // 处理返回值
            l1 = root;
        }else{
            root.left = l2;
            l2.right = root;
        }
        if(r1 == null){
            root.right = null;
            r2 = root;
        }else{
            root.right = r1;
            r1.left = root;
        }
        ret[0] = l1;
        ret[1] = r2;
        return ret;
    }
}

题解的方法更好！不需要显式的返回

class Solution {
    Node head,tail;
    public Solution(){
        head = null;
        tail = null;
    }
    public Node treeToDoublyList(Node root) {
        if(root == null)return null;
        dfs(root);
        head.left = tail;
        tail.right = head;
        return head;
    }
    void dfs(Node root){
        // head ...tail root...
        if(root == null)return;
        dfs(root.left);
        if(head == null)head = root;// 只修改一次
        else tail.right = root;
        root.left = tail;
        tail = root;
        dfs(root.right);
    }
}

剑指 Offer 37. 序列化二叉树

⭐剑指 Offer 38. 字符串的排列【全排列的高效去重方法】

class Solution {
    List<String> ans;
    int n;
    char c[];
    public String[] permutation(String s) {
        ans = new ArrayList<String>();
        c = s.toCharArray();
        n = c.length;
        dfs(0);
        return ans.toArray(new String[0]);
    }
    void dfs(int l){
        if(l == n){
            ans.add(String.valueOf(c));
        }
        HashSet<Character> nextc = new HashSet<Character>();
        for(int i = l;i<n;i++){
            // 对c当中的下一个字符
            if(nextc.contains(c[i]))continue;
            else nextc.add(c[i]);
            // 如果没有出现过，那么选择为当前的元素
            swap(l,i);
            dfs(l+1);
            swap(l,i);
        }
    }
    void swap(int i,int j){
        char temp = c[i];
        c[i] = c[j];
        c[j] = temp;
    }
}

🌱31. 下一个排列

ACM模板——排列 - 不重复全排列（DFS + 计数 + 附加规则）

day5

休息一下~

day6

剑指 Offer 39. 数组中出现次数超过一半的数字

剑指 Offer 41. 数据流中的中位数

基础方法：二分查找+Vector
1. 复杂度分析 O(logn + n) = O(n);
基础方法：kthmin
1. 复杂度 O(n)
排序的时间复杂度为 O(N logN)，但事实上，我们对除了中位数以外的其它位置的元素并不关心
1. 优先级队列
AVL树——借鉴二分查找的优点，并且防止退化

### 🌱AVL

剑指 Offer 42. 连续子数组的最大和

day7

剑指 Offer 43. 1～n整数中1出现的次数

写了一下午的代码……

class Solution {
    long[] bases;
    long[] base10;
    int i;
    void show(){
        for(int j = 0;j<=i;j++){
            System.out.println("base10["+j+"] = "+base10[j]+"; base["+j+"] = " + bases[j]);
        }
    }
    int findbase(int n){
        int l = 0,r = i;
        // 找到大于等于n的第一个区间
        while(l<r){
            int mid = (l+r)/2;
            if(bases[mid] < n)l = mid +1;
            else r = mid;// r = mid - 1; 必须配合 mid = (l+r+1)/2;
        }
        return l;
    }
    int getkth(int n,int base,int pos){
        int cur = -1;
        pos = base - pos;
        while(pos > 0){
            cur = n%10;
            n /= 10;
            pos --;
        }
        return cur;
    }
    public int findNthDigit(int n) {
        if(n==0)return 0;
        bases = new long[20];
        base10 = new long[20];
        bases[0] = 0;
        base10[0] = 1;
        i = 1;
        while(true){
            base10[i] = base10[i-1] * 10;
            bases[i] = bases[i-1] + i * (base10[i] - base10[i-1]);
            if(bases[i] > Integer.MAX_VALUE){
                bases[i] = Integer.MAX_VALUE;
                break;
            }
            i++;
        }
        show();
        int base = findbase(n);
        int off = (int)(n - bases[base-1] - 1);
        int rank = off/base;
        int trueval = (int)base10[base -1] + rank;
        System.out.println("base = "+base+" off = "+off+" rank = "+rank+" val = "+trueval+" k = "+(off % base));
        return getkth(trueval,base,off % base);
    }
}

class Solution {
    public int findNthDigit(int n) {
        int base = 1;
        long start = 1;
        long tot = 9;
        while(n>tot){
            n -= tot;
            base ++;
            start *= 10;
            tot = 9*start*base;
        }
        long num = start + (n-1)/base;
        // 获取数位的简单方法：字符串处理
        return Long.toString(num).charAt((n-1) % base) - '0';
    }
}

剑指 Offer 45. 把数组排成最小的数

Arrays.sort(ss,(x,y)->(x+y).compareTo(y+x));

⭐剑指 Offer 46. 把数字翻译成字符串【动态规划的优化】

动态规划的应用：多种可能性的转移 & 相互影响

不要着急一步到位，先做好分析

1 2 3 5 1 2 3 1 1

i i+1

dp[i] = dp[i-1] or dp[i-1] + dp[i-2];

令 x = dp[i-1]; y = dp[i-2];

public int translateNum(int num) {
    int x = num/10,y,a = 1,b = 1,c = -3,temp;
    while(num>=10){
        y = num %10;
        num/=10;
        x = num % 10;
        temp = x * 10 +y;
        if(10<=temp && temp <= 25){
            c = a+b;
        } else {
            c = a;
        }
        b = a;
        a = c;
    }
    return a;
}

剑指 Offer 47. 礼物的最大价值

剑指 Offer 48. 最长不含重复字符的子字符串

超棒的题解

🔑利用动态规划扩展区间

\[dp[i] = dp[i-1] +1 \\ dp[i] = i - map[j] \]

这种思想很类似于……

😂一时间竟想不到很好的例子

⭐剑指 Offer 49. 丑数【巧妙的递推方法】

只包含指定的质因子

首先想到了筛法，其实也是动态规划的一种体现

特判： i = 1

有一个问题：这个数可能很大，怎么有效控制空间？

可以考虑只存储有效数据，而不存储所有数据

更高效的思路是递推，而我做的其实还是记忆化搜索，空间浪费很大

每一个丑数都可以由之前的某个丑数生成（不一定唯一，比如 6 = 2*3 = 3*2)

其实应该用一个set维护所有的丑数集合

[1]

[1] + [2,3,5]

[1,2,3,5] + [4,6,10] 2乘以所有的因子

[1,2,3,4,5,6,10] + [6,9,15] 3乘以所有的因子

……

每一个丑数都必须由之前的一个丑数生成

如何依次产生每个丑数呢？

借鉴归并排序的思路

取最小值
1. p2,p3,p5分别对应 a2,a3,a5
2. nums[i++] = min(a2,a3,a5);
移动指针
1. 比如这个丑数是 a2 = p2*2;
2. p2++
3. 那么下一次 min(a2,a3,a5);肯定会把a3,a5当中的某个选出来，所以不会遗漏

😂313. 超级丑数

class Solution {
    int INF = 0x7fffffff;
    public int nthSuperUglyNumber(int n, int[] primes) {
        int k = primes.length;
        int[] pts = new int[k];
        int[] nums = new int[n];
        for(int i = 1;i<n;i++)nums[i] = INF;
        nums[0] = 1;
        for(int i = 1;i<n;i++){
            for(int j = 0;j<k;j++){
                nums[i] = Math.min(nums[i],nums[pts[j]]*primes[j]);
            }
            for(int j = 0;j<k;j++){
                if(nums[i] == nums[pts[j]]*primes[j]){
                    pts[j]++;
                }
            }
        }
        return nums[n-1];
    }
}

剑指 Offer 50. 第一个只出现一次的字符

day8

剑指 Offer 54. 二叉搜索树的第k大节点

剑指 Offer 55 - II. 平衡二叉树

如下代码是错误的

public boolean isBalanced(TreeNode root) {
    if(root == null)return true;
    else return Math.abs(d(root.left) - d(root.right))<=1;
}

反例

public boolean isBalanced(TreeNode root) {
    if(root == null)return true;
    else return isBalanced(root.left) && isBalanced(root.right) && Math.abs(d(root.left) - d(root.right))<=1;
}

这种方法的复杂度是 O(NlogN)（重复计算深度）

⭐短路先序遍历

dfs()的原生复杂度是O(N)，因此并不用担心。很多情况下dfs效率低下是因为重复访问某个节点

ms记忆化
vis标记
短路：返回查询值（一般和深度相关，本题就是深度），或者 BREAK_FLAG

都是不错的解决方法

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int INF = 0x3f3f3f3f,ERR = -INF;
    int h(TreeNode root){
        if(root == null)return 0;
        int l = h(root.left);
        if(l == ERR)return ERR;
        int r = h(root.right);
        if(r == ERR)return ERR;
        return Math.abs(l-r)<=1 ? Math.max(l,r) + 1:ERR;
    }
    public boolean isBalanced(TreeNode root) {
        return h(root) == ERR? false:true;
    }
}

⭐剑指 Offer 51. 数组中的逆序对

🔑归并排序模板

剑指 Offer 56 - I. 数组中数字出现的次数

剑指 Offer 56 - II. 数组中数字出现的次数 II

⭐剑指 Offer 57 - II. 和为s的连续正数序列

尺取

剑指 Offer 58 - II. 左旋转字符串

😂

(s+s).substring(k,k+s.size());

day9 & 10

剑指 Offer 59 - II. 队列的最大值

🔑尺取区间最大值——单调队列

class MaxQueue {
    Queue<Integer> q;
    Deque<Integer> qmax;
    public MaxQueue() {
        q = new LinkedList<Integer>();
        qmax = new LinkedList<Integer>();
    }
    
    public int max_value() {
        if(!q.isEmpty())return qmax.peekFirst();
        else return -1;
    }
    
    public void push_back(int value) {
        q.offer(value);
        while(!qmax.isEmpty() && qmax.peekLast() <= value){
            qmax.pollLast();
        }
        qmax.offerLast(value);
    }
    
    public int pop_front() {
        if(q.isEmpty()){
            return -1;
        }else{
            int front = q.poll();
            if(front == qmax.peekFirst()){
                qmax.pollFirst();
            }
            return front;
        }
    }
}

💡这种题目，应该最先考虑同构的数据结构，这样可以基本保持动态操作的相对一致性

比如这里的单调队列，以及单调栈

单调队列利用到的性质是最大值的排他性，即后面的最大值会打败所有之前不如它的值

剑指 Offer 60. n个骰子的点数

最先想到的还是记忆化搜索

class Solution {
    int[][] poss;
    int ms(int n,int tar){
        if(n<0 || tar >6 *n || tar <n)return -1;
        if(poss[n][tar]!=0)return poss[n][tar];
        
        for(int i = 1;i<=6;i++){
            int r = ms(n-1,tar-i);
            if(r!=-1){
                poss[n][tar] += r;
            }
        }
        return poss[n][tar];
    }
    public double[] twoSum(int n) {
        poss = new int[6*n +10][6*n + 10];
        for(int i = 1;i<=6;i++){
            poss[1][i] = 1;
        }
        double base = 1;
        for(int i = 0;i<n;i++){
            base *= 1/6.0;
        }

        double[] ans = new double[5*n+1];
        for(int i = n;i<=6*n;i++){
            ans[i-n] = ms(n,i) * base;
        }
        return ans;
    }
}

🔑滚动数组优化 / `dp[n] = f(dp[n-1])` 类型

class Solution {
    public double[] twoSum(int n) {
        double[] dp = new double[6*n +10];
        for(int i = 1;i<=6;i++){
            dp[i] = 1/6.0;
        }
        // 1-n个骰子
        for(int i = 2;i<=n;i++){
            // 对于每一个可能出现的结果（从后向前，类比完全背包）
            for(int j = 6*i;j>=i;j--){
                // 初始化，因为i-1个骰子对应的dp值已经不会再使用了
                dp[j] = 0;
                // 假设第i个骰子投出的数字分别是1-6
                for(int k = 1;k<=6;k++){
                    int pre = j-k;
                    // 如果这个数字可以由i-1个骰子产生
                    if((i-1)<=pre && pre<= 6*(i-1)){
                        // 累加结果
                        dp[j] += dp[pre]/6.0;
                    }
                }
            }
        }
        // 返回数组切片
        return Arrays.copyOfRange(dp,n,6*n+1);
    }
}

总结

若有恒，何必三更眠五更起

最无益，莫过一日曝十日寒

还是用这句话激励自己吧！有时候自己也不喜欢看过题解或者找到一个朴素的实现就浅尝辄止，刷够题目本身不是算法的意义和乐趣，分析和解决问题才是🎉

很多时候把什么事情看作任务，反而不太容易坚持，不如把思考算法问题也当作一个娱乐的方式，快乐学习🕺

Do it better with pleasure:happy:

希望你每做一个题都有自己的思考，都有收获🏃

LeetCode 精选 TOP 面试题 145

100 天后 2020年11月28日星期六记得来打卡！

我们都会有美好的未来！

posted @ 2020-11-06 20:52 ZXYFrank 阅读(162) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

Enjoy the process🍀