概率论与数理统计基本概念

📚 Takeaways

需要建立起来的认识

• \[D(X) = 0 \to P(X = \text{const}) = 1 \]

  概率为1并不代表是必然事件，概率为0不代表是不可能事件

• 伯努利大数定律（独立重复试验）是频率近似概率的基础

• 中心极限定理刻画了样本和总体的关系

• 后验概率小于先验概率

Axioms

• \[0\leq P \leq 1 \]

• \[P(S) = 1 \]

  s denotes sample space

• when exclusive

\[P(\bigcup E_i) =\sum P(E_i) \]

普适规律

• Bayesian Rule

\[ P(A|B) =P(B|A)\cdot \frac{P(B)}{P(A)} =P(A) \cdot \frac{P(B|A)}{P(B)} <=P(A) \]

• Inclusion-exclusion principle 容斥原理

  

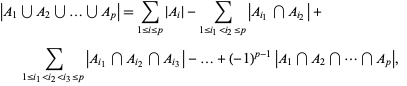
• Conditional Probability

\[P(A|B) = \frac{P(AB)}{P(B)} \]

后验概率 P(p|data)

一枚硬币，扔了一亿次都是正面朝上，再扔一次反面朝上的概率是多少？

The data is just the result of observation.

What exactly does it tell us

It depends on our assumption

随机事件和概率

常见概型

分配问题 / 隔板法

普适公式

1. 逆概率

2. 加法（容斥原理）

3. 减法

4. 全概率公式

5. 贝叶斯公式

条件概率

随机变量的函数

随机变量的可加性

例题

事件的独立性

不可能事件与任何事件既独立又互斥！

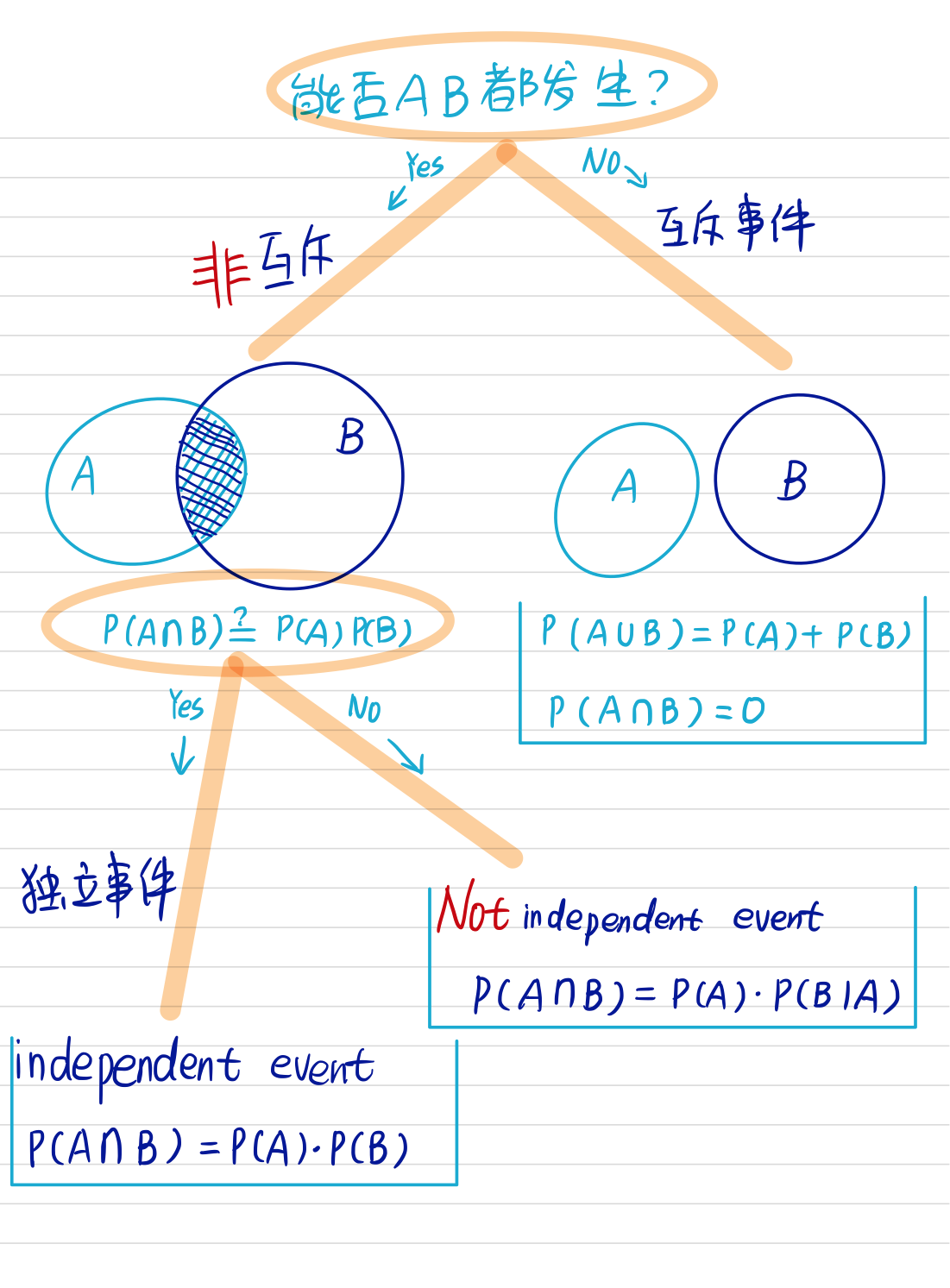
独立随机变量的最大值 / 最小值的概率

随机变量的数字特征

期望 方差 标准差

方差和期望的关系

\[D(X) = E(X-E(X))^{2} = E(X^2) - E^2(X) \]

协方差

切比雪夫不等式

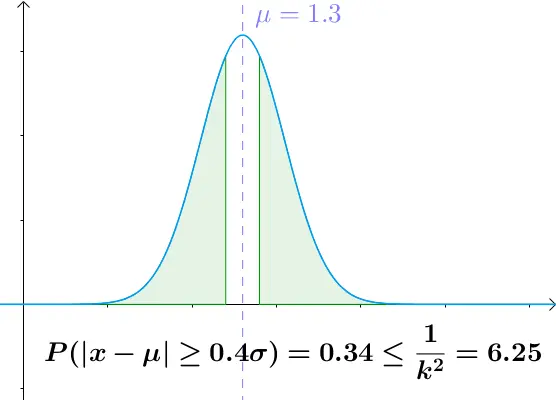
\[P(|X-\mu|\geq \varepsilon)\leq \frac{\sigma ^2}{\varepsilon^2} \]

随机变量的拆分

一维分布

总结

常见概率分布的直觉与联系 - 论智的文章 - 知乎
https://zhuanlan.zhihu.com/p/47609519

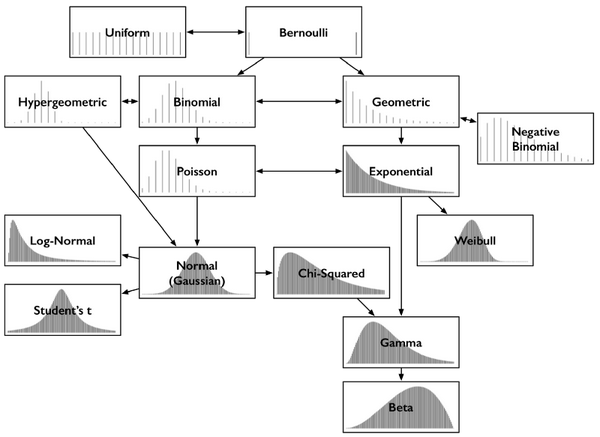
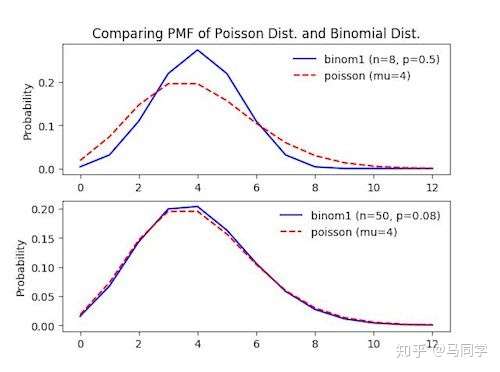
二项分布/泊松分布

二项分布和二项式展开 / 组合数有直接联系

二项分布的期望的物理意义

成功次数 = λ

\[p = \frac{\lambda}{n}\\ \lambda = \frac{1}{\mu} = np = E(B(n)) \]

知乎：泊松分布的极限理解

几何分布/指数分布

• 无后效性

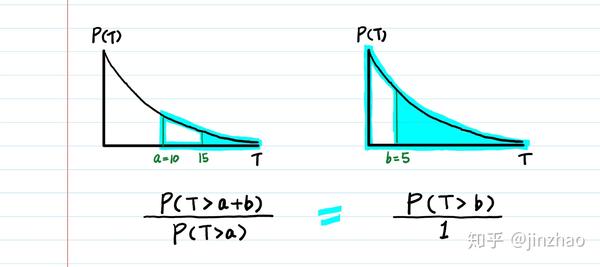
• 几何分布

\[ P(n = k) = p(1-p)^{k} \]

• 指数分布

\[ p(t = x) = \lambda e^{-\lambda x} \]

• 指数分布是几何分布的连续化

\[ \lambda = np\\ p = \frac{\lambda}{n} \]

当进行极多次独立重复试验之后

\[ p(x) = \lim_{n\to\infty}p(1-p)^{x} \]

没有出现n，替换一下

\[ p(x = \frac{k}{n}) = \lim_{n\to\infty}p(1-p)^{x} = \lim_{n\to\infty}\frac{\lambda}{n}(1-\frac{\lambda}{n})^{x} \\ = \lim_{n\to\infty}\frac{\lambda}{n}[(1-\frac{\lambda}{n})^{ n \cdot\frac{k}{n}}] = \lim_{n\to\infty}\frac{\lambda}{n}[(1-\frac{\lambda}{n})^{ n \cdot x}] = \lim_{n\to\infty}\frac{\lambda}{n}[n\cdot e^{-\lambda \cdot x}] = \lambda e^{-\lambda x} \]

刻画随机事件两次发生时间间隔

无记忆性的分布一定是指数分布 / 几何分布

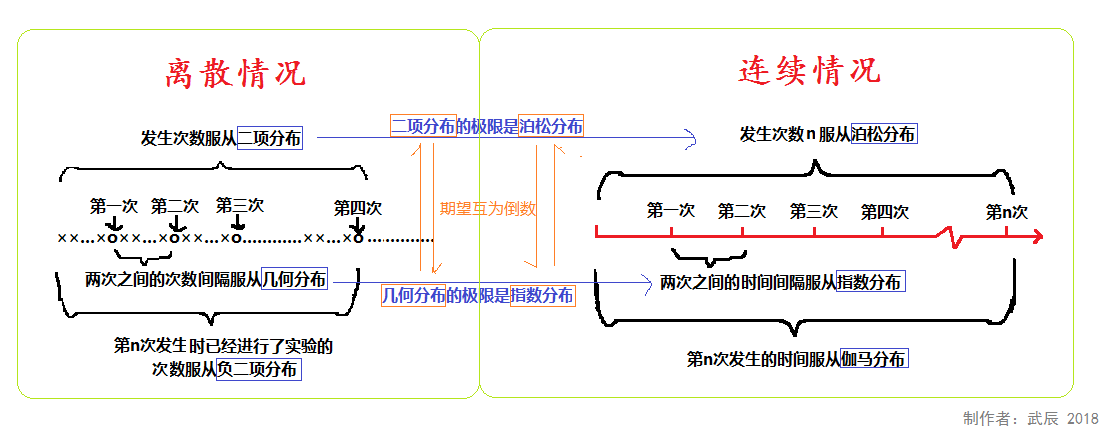
几何分布 / 超几何分布 的意义

• 几何分布：
• 超几何分布：不放回抽样

正态分布

大数定律&中心极限定理

依概率收敛

大数定律

辛钦——独立同分布 & 存在期望

\[\frac{1}{n}\sum_{i = 1}^{n}X_i\xrightarrow[]{P} E(X) \]

切比雪夫——独立&方差存在一致有上界

\[\frac{1}{n}\sum_{i = 1}^{n}X_i\xrightarrow[]{P} \frac{1}{n} \sum_{i = 1}^{n}E(X_i) \]

伯努利大数定律：频率代替概率

伯努利试验：独立重复试验

ξ指示试验是否成功

\[\frac{1}{n}\sum\xi_i \xrightarrow[]{P}\mu \]

列维-林德伯格中心极限定理——独立同分布&均值方差存在

\[\frac{1}{n}\sum_{i = 1}^{n}X_i \sim N(\mu,\sigma^2) \]

棣莫弗-拉普拉斯定理——二项分布渐进正态分布

\[Y_n\sim B(n,p) \\ \lim_{n\to \infty}Y_n \sim N(np,\sqrt{np(1-p)}) \]

---

数理统计

总体和样本

统计量的均值和方差

\[E(X_i) = \mu \\D(X_i) = \sigma^2\\ E(\overline{X}) = E(X) = \mu \\ D(\overline{X}) = \frac{\sigma^2}{n} \\ E(S^2) = \sigma^2 \]

假设检验

在不能穷举的情况下，不能靠举例子来证明一个命题是正确的，但是可以靠举出一个反例来证明一个命题是错误的。

• 显著性水平

  \[\alpha = 1-p \]

• 置信区间