线性代数基本概念

线性代数概念的理解

Vector / Matrix

What’s a vector?

向量实际上是具有n 维属性的一个较为复杂的客观实体

\[x = \{x_1,x_2,...,x_n\} \]

Linear transformation——矩阵的本质

n阶矩阵 A相似对角化的充要条件

• 有n个线性无关的特征向量
• 每个 k重特征值都有k个线性无关的特征向量

相似对角化的充分条件

• A有n个不同的特征值
• A是实对称矩阵

矩阵实际上代表一个线性变换

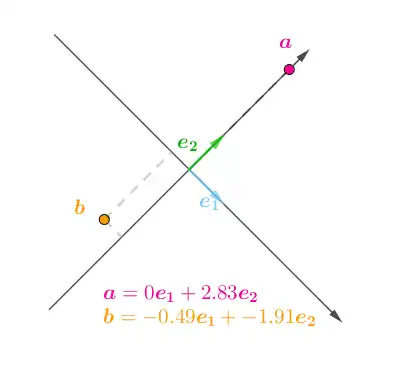
Basis

Basis

一组可以张成该空间的，线性无关的向量的集合称为一组基

Dimension

The number of vectors in any basis of V is called the dimension of V, and is written dim(V).

Bases as Coordinate Systems

Row-Echelon Form 行阶梯型

使用高斯消元法的浮点数操作总量都在 O(n2)双重循环

Reduced REF

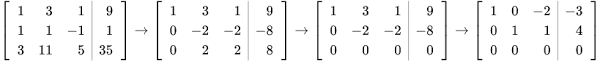
Span 张成的子空间

线性组合

\[S\left( {{\alpha _1},...,{\alpha _n}} \right) = \left\{ {\sum\limits_{i = 1}^n {{c_i}{\alpha _i}\;|\;{c_i} \in \mathbb{R}} } \right\} \]

which is the set of all linear combinations of the vectors in this subspace.

Column Space 列空间

列向量的所有线性组合的集合构成的子空间

Row Space

Null Space (Kernel) 零空间 & Nullity

Intuative Theorems

\[\dim(\text{rowspace}(A)) = \dim(\text{colspace}(A)) = \text{rank}(A) \\ \text{rank}(A) + \text{nullity}(A) = n \]

Rank

列空间的维数叫做秩

The number of dimensions in the column space.

为什么行秩 = 列秩？

为什么行空间和列空间维数相等？

Elementary row operations, which by construction don't alter the row rank

Linearly Dependent 线性相关

at least one of the vectors in the set can be written as a linear combination of the others.

n阶矩阵“不降维”的充分条件

• 满秩
• 特征值不为0
• 有n个特征值
• 行列向量线性无关
• 齐次方程组有唯一零解
• ……

Transformation

线性变换的原理

二次型的意义是什么？有什么应用？ - 马同学的回答 - 知乎

线性变换，实质上是对基的变换，引起了空间的线性变换。

那么，没有平移，空间的变换一定可以描述为拉伸+旋转（想象一个参照点被移动的过程）

Non Square Matrices 非方阵

广义上说，矩阵是空间之间的线性变换。方阵对应在平面之内的变换（若特征值为0，则会出现降维情况）。

非方阵代表空间之间的线性（等距分布）映射

对于一个矩阵来说，可以理解列空间是目标空间

• 3*2 矩阵
  • 二维到三维
  • 列满秩

• 2*3 矩阵
  • 三维到二维
  • 非列满秩（降维）

Determinant 行列式 / 决定式

🤔 为什么行列式被叫做这个名字？

我一直觉得翻译为确定式或者决定式比较恰当。中文叫行列式应该是出于形状的考虑，因为determinant的形状就是几行几列的数表，另外也可能是受到日本翻译的影响，日本把determinant成为行列式，把matrix称为行列

行列式为什么称作“行列式”？ - fever wong的回答 - 知乎
https://www.zhihu.com/question/332671271/answer/733861760

理解成“决定式” / “不变式”更合理

表征了线性变换的总体效应度量

Rank 秩

线性变换得到的子空间的维数

Rank-One Decomposition

Inverse Matrix

存在条件

\[\text{rank}(A) \neq 0 \]

The Moore-Penrose Pseudoinverse——MP逆

广义逆

基于 SVD的求法

\[(ABC)' = C'(AB)' = C'B'A'\\ (X_1X_2...X_n)' = X_n'(X_1X_2...X_{n-1})' \]

对于线性方程组 Ax = y

• When A has more columns than rows, then solving a linear equation using the
  pseudoinverse provides one of the many possible solutions. Specifically, it provides
  the solution x = A+ y with minimal Euclidean norm ||x||2 among all possible
  solutions.
• When A has more rows than columns, it is possible for there to be no solution.
  In this case, using the pseudoinverse gives us the x for which Ax is as close as
  possible to y in terms of Euclidean norm ||Ax − y||2.

Similarity

:happy:similar matrices do the same thing in different coordinate systems (with the help of BASIS TRANSOFRMATION)

知乎：同一个线性变换（结果相同）在不同的基中对应的变换矩阵（实际上是一种形式），称为相似矩阵

Interactive examples

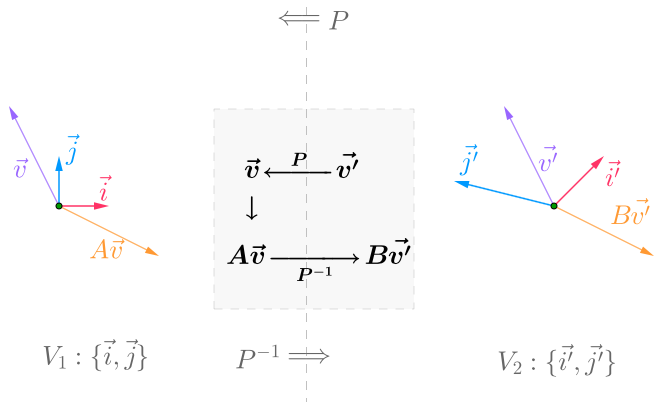
Eigen Value & Eigen vectors

特征值的意义

• 单独存在
  • 特征值可以得到行列式

\[Ax = \lambda x\\ A(kx) = \lambda (kx) \]

一个特征值对应无穷多特征向量

🤔Eigen is a German word meaning "own" or "typical"

\[Ax = \lambda x\\ \exists x \neq \to|A-\lambda|x = 0 \\ \]

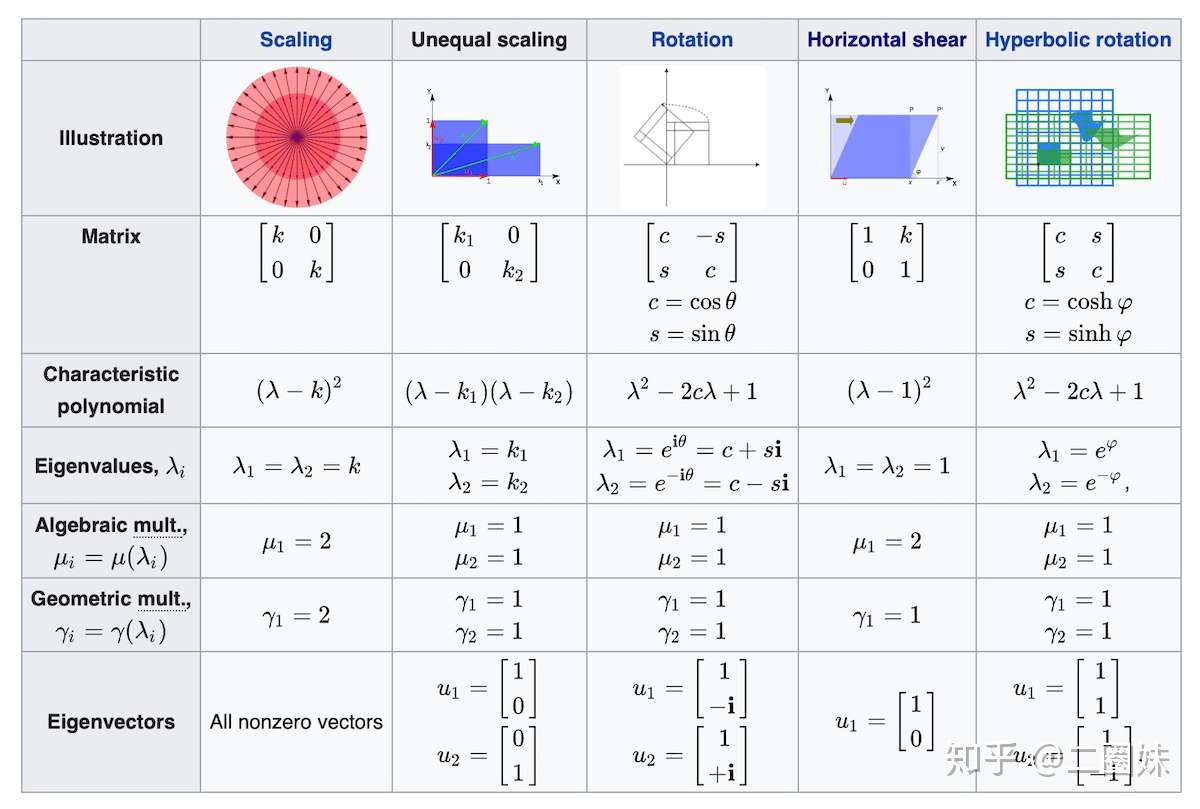
Properties

Eigenvalues

\[\prod_{i = 1}^{n}\lambda = |A|\\ \sum_{i = 1}^{n}\lambda = \text{Tr}(A) \]

Eigenvectors

1. k重特征值至多有k个线性无关的特征向量

2. 不同特征值对应的特征向量线性无关

3. 同一个特征值的特征向量有无数个

4. 不同非零特征值对应的非零特征向量的线性组合不是特征向量

What if there are complex eigenvalues

Interactive Illustartion : Complex Eigenvalues

⭐They come in pairs

As a consequence of the fundamental theorem of algebra as applied to the characteristic polynomial, we see that:

Every n×n matrix has exactly n complex eigenvalues, counted with multiplicity.

Rotation-Scaling Theorem

the essence of the complex eigenvectors and eigenavalues is that it

eigenvector generates the basis transformation

eigenvalue performs the action(rotation and scaling)

Youtube:Geometry of Real and Complex Eigenvalues

\[\lambda = a+ib \\ {\bf{\xi}} = x+iy\\ \\(a,b,x,y \in \R) \\ \]

\[A\xi = \lambda \xi\\ Ax + iAy = (ax-by)+i(ax+by)\\ \]

\[1.Ax = ax-by \\ 2.Ay= ax+by \\ A = \left( \begin{matrix} a & b\\ -b &a \end{matrix} \right) \]

That's to say, the A matrix rotates and stretches x & y(the vectors in real and imaginary parts of the eigen vectors.

Geometrically, the rotation-scaling theorem says that a 2×2 matrix with a complex eigenvalue behaves similarly to a rotation-scaling matrix.

❗ So, actually the PLANE spaned by x,y(components in Re/Im part of the complex eigen vector) remains kind of invariant.

Interactive math: similarity to rotation

the effect of lambda’s norm

1. the Re and Im part determine 2 basis vector that’s gonna be rotated and stretched
   1. or you can say that they defined the basis transformation
2. the
   1. 
   2. 
   3. 

❗如何理解特征值的“吸引”作用](https://www.zhihu.com/question/21874816/answer/181864044)

Derivatives

Trace

迹是一种算子 = 特征值的和

\[\text{Tr}(A) = \sum\lambda \]

\[||A||_{F} = \sqrt{\text{Tr}(AA^{T})} \]

求导法则

迹技巧

注意第2步

机器学习中的数学理论1：三步搞定矩阵求导 - 科技猛兽的文章 - 知乎

例子

Decompositions

LU分解

解方程方便。本质上，LU分解是高斯消元的一种表达方式。首先，对矩阵A通过初等行变换将其变为一个上三角矩阵。

1. 矩阵是方阵（LU分解主要是针对方阵）
2. 矩阵是可逆的，也就是该矩阵是满秩矩阵，每一行都是独立向量
3. 消元过程中没有0主元出现，也就是消元过程中不能出现行交换的初等变换

QR 分解

任何的实方阵都可以做QR分解 => 正交矩阵 + 上三角

The Q contains the orthonormal vectors, while the R tracks all the changes we have made

Householder Reflections / Givens Rotation

1. Givens Rotation/Householder Reflections
2. 如何理解Householder变换和Givens旋转? - 荆哲的回答 - 知乎

Householder Reflections

把A矩阵看做是n个m维向量，通过一次Householder变换就可以把第一个向量除了第一个元素外的其他元素都变为0。

• 镜面反射
• Cornell Brilliant Tutorial!
• 

\[\underline{x} - 2\frac{\underline{v}^T\underline{x}}{\underline{v}^T\underline{v}} \underline{v} = \underbrace{\left(I - 2\frac{\underline{v}\,\underline{v}^T}{\underline{v}^T\underline{v}}\right)}_{\text{Householder relfection}}\underline{x}, \]

• 
• Geometry

Givens Rotation O(1)时间贪心地处理矩阵的每一个元素 进行O(n^2)次

• 

Gram-Schmidt orthogonalization

Gram-Schmidt is not a stable algorithm for computing the QR factorization of A because of rounding in floating point arithmetic.

如何理解施密特（Schmidt）正交化 - YourMath的文章 - 知乎

UCLA - GramSchmidt for QR

满秩分解

任何非零矩阵一定存在满秩分解

Eigen Decomposition / Diagonalization

相似对角化左右两侧是特征向量构成的可逆矩阵

矩阵的对角化不唯一

也可以作“特征基变换”理解

对于一个矩阵 A ，取特征向量，作为desired basis

相似对角化的充要条件

n阶矩阵 A

1. 有n个线性无关的特征向量
2. 每个 k重特征值都有k个线性无关的特征向量

相似对角化的充分条件

1. A有n个不同的特征值
2. A是实对称矩阵

Spectral Decomposition(谱分解)

谱分得到的是正交的特征向量矩阵

pdf ref- ucsd

Positive definite (正定)

正定矩阵的概念来源于二次型

\[\lambda>0\\ \text{can guarantee that } \\ \forall x \ x^{T}Ax>0 \]

正定矩阵的性质

• 特征值全为正
• 各阶顺序主子式都为正
• 合同于单位阵

实对称矩阵的特点

1.实对称矩阵A的不同特征值对应的特征向量是正交的（可以进行谱分解）

2.实对称矩阵A的特征值都是实数，特征向量都是实向量。

3.n阶实对称矩阵A必可对角化，且相似对角阵上的元素即为矩阵本身特征值。

4.若λ具有k重特征值　必有k个线性无关的特征向量，或者说必有秩r(λ0E-A)=n-k，其中E为单位矩阵。

实对称矩阵是正定矩阵的充分必要条件是它的所有特征值都大于0

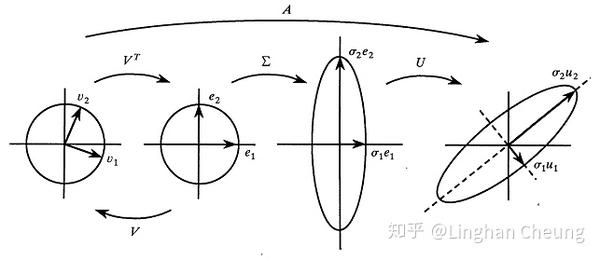
Singular Value Decomposition (SVD)

• 奇异值
• 左右奇异向量（正交）

requirements

\[[U,S,V] = \text{svd}(A) \\ A_{m\times n} = U_{m\times m}S_{m\times n}V_{n\times n}^{T} \]

^[1]

Essence & Geometry

任何一个矩阵都等效于一个线性变换

线性变换无法移动原点

1. 
2. 
3. 

• 
• 

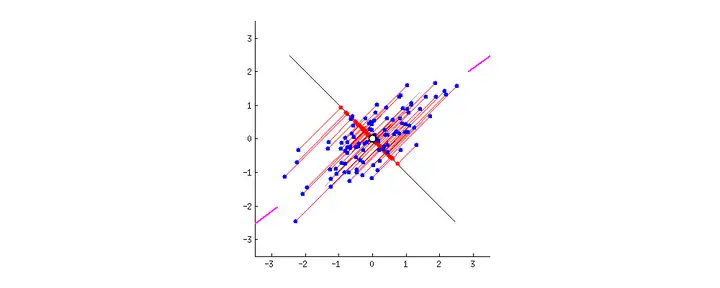
Application:Principle Component Analysis(PCA)

一种线性、全局、非监督降维方法，基于特征值分解

最小化初始点（中心化之后）和映射到新维度的新坐标点的距离平方之和

PCA can be perceived as a task of find some encoding function that produces the code
for an input, f(x) = c, and a decoding function that produces the reconstructed
input given its code, x ≈ g(f (x)).

^[1:1]

类似的还有 LCA（有监督降维方法）

zhihu

Spaces 空间

Categories

希尔伯特空间、内积空间的定义有什么关系和区别？ - 李狗嗨的回答 - 知乎
https://www.zhihu.com/question/332144499/answer/731866608

Metric Space 度量空间

定义了抽象距离的空间称作度量空间

一个度量 d满足

1. 正定性： ，且 当且仅当 成立;
2. 对称性： ;
3. 三角不等式： .

Vector Space 向量空间

八大定律

Don't take these axioms too seriously! Math is not about axioms, despite what some people say. Axioms are one way to think precisely, but they are not the only way, and they are certainly not always the best way. Also, there are a number of ways to phrase these axioms, and different books will do this differently, but they are all equivalent (unless the book author was really sloppy).

向量空间的定义中并不包含向量与向量之间的乘法。而这也是正是内积作为区别内积空间与一般向量空间的附加条件的原因。

向量空间和度量空间的区别

向量空间是赋予代数结构，度量空间是赋予拓扑结构。

向量空间（vector space）的定义包含五个要素：集合 ，域 ，向量加法 ，数量乘法 ，还有 满足的八条公理。这个定义里的要素跟「拓扑」，「度量」，「范数」，「内积」都没有关系。

度量空间（metric space）的定义包含两个要素：集合 ，度量函数 。这个定义里， 不需要有线性结构。在一般的度量空间里， 这样的表达式没有意义。

---

Normed (Linear) Space 赋范（线性）空间

定义了向量的大小：范数

范数常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。其定义是：

设 是布于一个域 （例如，实数域 、复数域 ）的向量空间，函数 作用于，且满足条件：

1. 正定性：对 ；且 当且仅当；
2. 齐次性：对，有 ;
3. 三角不等式：对 ，有 。

Inner Product Space 内积空间

向量空间添加了新的运算：内积

内积空间具有基于空间本身的内积所自然定义的范数， ，且其满足平行四边形定理，也就是说内积可以诱导一个范数，所以内积空间一定是“赋范空间”。

内积将一对向量与一个纯量连接起来，允许我们严格地谈论向量的“夹角”和“长度”，并进一步谈论向量的正交性。

Projection

MIT Matrix Projection

\[p = Pb = A\hat{x}\\ (\hat{x} \text{ is the coord., }A\text{ is the base of a subspace})\\ e = b-p\\ \]

\[(a_1,a_2)^T\cdot (b-p) = 0\\ A^T(b-A\hat{x}) = 0\\ A^TA\hat{x} = A^Tb \]

左乘 (ATA)-1

\[\hat{x} = (A^TA)^{-1}A^Tb\\ \]

左乘A

\[A\hat{x} = Pb = A(A^TA)^{-1}A^T\cdot b\\ P = A(A^TA)^{-1}A^{T} \]

性质

• \[P^T = P \]

• \[P^2 = P \]

最小二乘

左零空间（转置的零空间）

\[xA = 0的特解 \]

\[P = A(A^TA)^{-1}A^{T}\\ e = Eb = (I-P)b\\ eA = 0 \]

I-P可以得到左零空间当中的b的垂直分量

最小二乘法拟合

Least Squares Approximations _ MIT

It often happens that Ax = b has no solution. The usual reason is: too many equations.
The matrix has more rows than columns. There are more equations than unknowns
(m is greater than n).

\[Ax = b\ 无解 \\ x = \mathop{\arg\min}_{\theta} |Ax-b|^2 \]

\[\text{column space of A is exactly the 2d plane} \]

---

1. Ian GoodFellow et al., Deep Learning, MIT the e-Book from GitHub ↩︎ ↩︎