微积分基本概念
一个我们可以思考的问题
世界是离散的，还是连续的？
-
微积分与概率论
关于世界是「离散」还是「连续」的这个问题，让我想起了另一个类似范畴的讨论，即这个世界是「概率的」（statistics）还是「微积分的」（calculus）。再换个角度说，世界是「不确定的」（indeterminate）还是「确定的」（determinate）。
在确定性的世界里，微积分是至高规则。你可以通过设置参数、推导过程、运用公式...准确地计算一件事。比如，当你想发火箭到月球上，你需要的是微积分的思维——这意味着你必须每时每刻都知道火箭在哪儿，精确地预测整个过程。而不是，先发射，路上再慢慢调整。
而在不确定的世界里，概率论才是解释世界的方法。你无法精确预知一件事的过程和结果，你能做的仅是，通过收集足够多的样本，观察结果的分布，来预测某件事情「有多大可能」会「产生某种结果」。
作者：张潇雨 链接：https://www.zhihu.com/question/21075436/answer/56329703 来源：知乎 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
📖 Takeaways
数学由离散走向了连续
微积分
- Continuity 连续
- Limit 极限
- “趋近”
- Differential Calculus 微分
- Derivative 导数
- 瞬时变化率
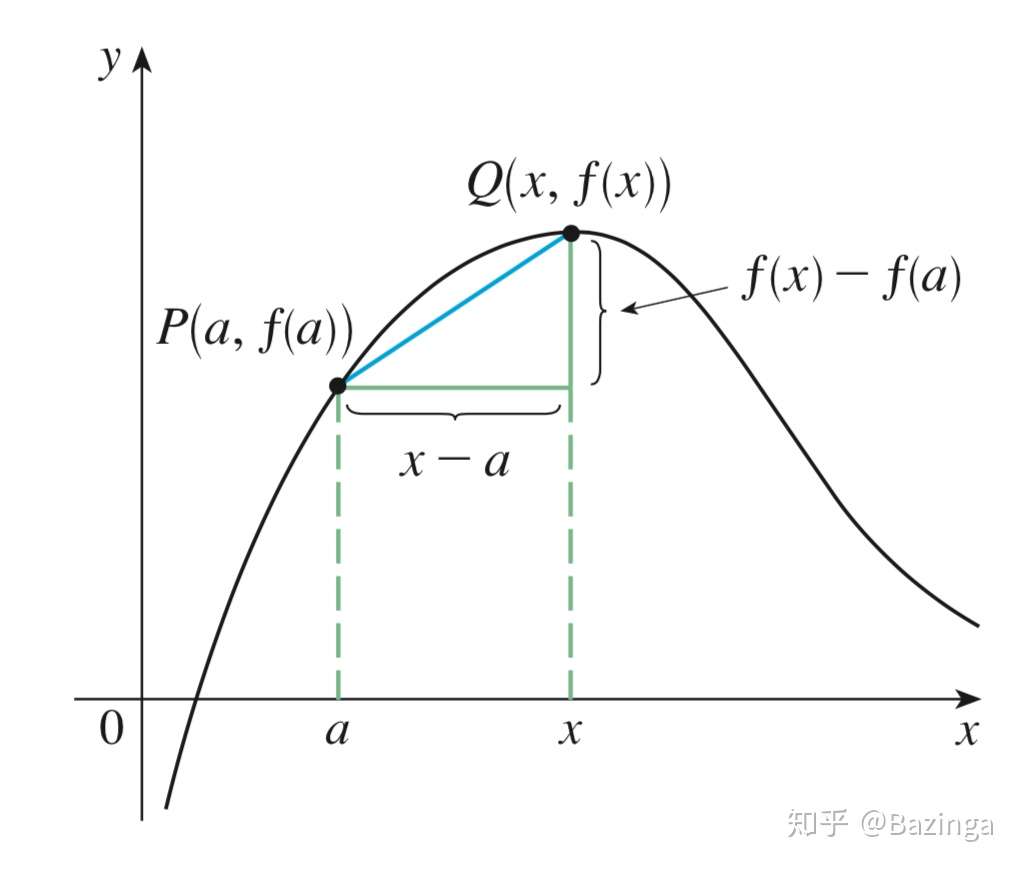
- Differentials 微分
- 以直代曲
- Derivative 导数
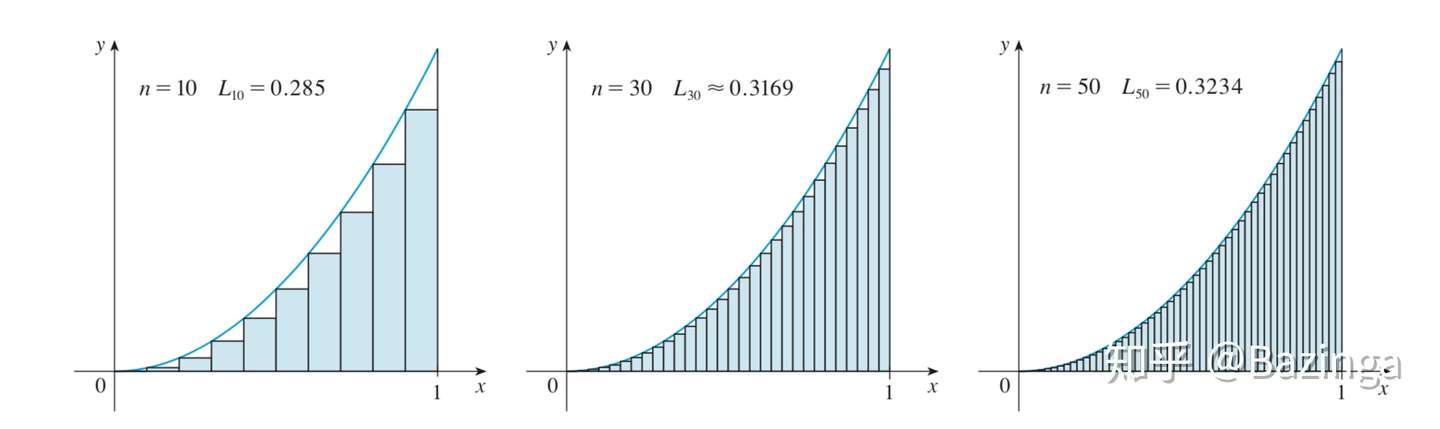
- Integral Calculus 积分
- Integral
- Integral
需要建立的概念
- rates of change 变化率
- 极限
- 近似
熟知的典型应用
- Gradient Descent 梯度下降法
极限与连续
数列存在极限的存在准则
- 单调有界
- 夹逼
函数极限
- 邻域 左右极限
- 充要条件
无穷小与无穷大
无穷小的比阶
不是所有的无穷小都可以比阶
无界量
- 无界量不一定是无穷大量
\[f = x\sin x
\]
间断点
-
第一类
- 可去
- 跳跃
-
第二类
- 无穷间断点
- 震荡 sin(1/x)
连续
连续
微分学
可导与连续
- 可导一定连续
- 但不一定在一个邻域内连续
\[y = x^2D(x)
\]
(Direclet)
一元函数可微与可导互为充要条件
高阶导数的求解
- 莱布尼茨公式
- 幂级数——函数展开式的唯一性
参数方程的二阶导数
反函数的二阶导数
变限积分求导公式
一元函数微分学的应用
极值和最值
最值点不一定是极值点（端点 / 常函数）
极值点不一定是最值点
多元函数闭区间唯一极值点不一定是最值点（马鞍面）
通过保号性判断极值
渐近线
函数取值范围问题
中值定理
有界最值定理
介值定理 IVT 😂
注意介值定理的条件：闭区间连续
-
-
问题的抽象
- 合理选择变量
- 椅子腿和地面的距离之和的差值
\[f(x)\cdot g(x) = 0 \\ f(x), g(x) \geq 0 \] -
构造函数
\[h(x) = f(x) - g(x)\\ \exists x_0 \to h(x_0) = 0 \\ 此时 f(x_0)\cdot g(x_0) = f(x_0) ^2 = g(x_0)^2 = 0 \\ 因此有 \ f(x_0) = g(x_0) = 0 \]
-
均值定理（可由介值定理导出）
费马定理（保号性）
罗尔定理
罗尔定理的多次使用
拉格朗日中值定理
柯西中值定理推导拉格朗日定理
积分中值定理
泰勒公式
零点问题、微分不等式
零点
罗尔定理的推论：n阶导数至多有k个根，f(x)至多有 k+n 个根
实系数奇次方程至少有一个实根（零点定理）
积分
定积分
反常积分
充分条件
- 连续
- 有界，有有限个间断点
- 单调
必要条件：有界
反常积分
- 无界
- 无穷
反常积分存在不一定极限等于零
积分的计算
分部积分公式
积分的几何应用
面积
- f1x-f2x
- 曲边扇形
体积
积分等式和不等式
多元函数微分
点集的基本概念
-
邻域 / 去心邻域
-
内点
-
边界点
-
有界集 / 无界集
-
开集 / 闭集
可以由原点的一个邻域囊括
-
联通集
极限的存在性
偏导数
本博文本意在于记录个人的思考与经验，部分博文采用英语写作，可能影响可读性，请见谅
本文来自博客园，作者：ZXYFrank，转载请注明原文链接：https://www.cnblogs.com/zxyfrank/p/calculus-basic.html
