Bayes Theorem

目录

• 相关概念
  • 独立
  • 条件独立
• 基本简化 Naive Bayes Assumption
• 贝叶斯公式
  • ESSENCE 🌹
  • Upper Bound = 1 -> Total Probability Rule
  • Bayes Multiplier
• 概率
  • 概率的研究对象是样本空间
• 似然
  • 似然的研究对象是参数空间
  • 凭什么说 L(θ|x) = f(x;θ)
    • 似然函数不是参数的概率分布
    • 似然函数和概率密度pdf的关系
• Bayes formula
  • 由来——公理化
  • 贝叶斯估计当中参数先验分布的作用
• 机器学习当中的 MLE，MAP，BaBesian
  • 如何使用贝叶斯方法估计参数——使用似然函数
• 🔑例题
• Thinking, Fast and Slow
• Monty Hall Problem
  • 我先自己尝试一下😂
  • Switch
• 男孩女孩
  • 我的答案
  • 李永乐老师的解答
    • 至少一个是女孩 P = 1/3
    • 第一个是女孩 P = 1/2
• 三囚犯问题
  • • 我的答案
• ref

相关概念

符号

\[P(A|B) 条件概率\\ P(A,B) = P(A\cap B)联合概率 \\ P(A,B) \leq P(A|B) \]

独立

指的是两个变量之间没有相互干扰

\[P(A,B) = P(A)P(B|A) = P(A)P(B)\\ P(B|A) = P(B) \]

条件独立

某个条件之下的独立

\[P(A,B|Z) = P(A|Z) \ast P(B|Z) \]

https://zhuanlan.zhihu.com/p/90984141

知乎关于独立性和条件独立性的解释

无论事件 是否独立，我们都可以通过建立特殊的事件 ，使得事件 关于事件 条件独立。

条件独立实质上改变了考虑问题的空间

For example, suppose that the English words are all conditionally independent given . In other words, the probabilities of seeing two words are independent given that a message is spam. This is clearly an oversimplification, as the probabilities of the words “pills” and “buys” are clearly correlated;however, for most words (e.g. “penguin” and“muffin”) the probabilities will indeed be independent,and our assumption will not significantly degrade the accuracy of the model.

基本简化 Naive Bayes Assumption

条件就是变量，在应用条件概率公式时，消除关于变量的先验条件概率的组合爆炸问题

\[P(B,x_1,x_2,...,x_n) = P(B,A) = P(B)\mathbf{P(A|B)} =P(B) \cdot \Pi P(x_i | B) \]

贝叶斯公式

ESSENCE 🌹

\[\\ \textbf{Bayesian Theorem | E: Evidence H: Hypothesis}\\ P(H|E) = \frac{P(H) P(E|H)}{P(E)} = P(H)\frac{P(E|H)}{P(E)} = \frac{P(HE)}{P(HE)+P(HE^c)} \]

贝叶斯公式的计算结果，实际上是做了样本空间的调整

Upper Bound = 1 -> Total Probability Rule

\[P(A) = P(AB) + P(AB^c) \]

\[P(B|A) = \frac{P(A|B)P(B)}{P(A)} = \frac{P(AB)}{P(A)} \leq\frac{P(AB)}{P(AB) + P(AB^c)} \leq 1 \]

Bayes Multiplier

\[P(B|A) = \frac{P(AB)}{P(A)} = P(B)(先验)\frac{P(A|B)}{P(A)} = P(B) \cdot\lambda \]

\[\frac{P(A|B)}{P(A)} = \frac{P(AB)}{P(A)P(B)} \in \ ?\\ \]

• Bayes Multiplier 贝叶斯乘数
• 因为贝叶斯乘数大小不确定，所以先验概率和后验概率的大小没有必然联系

---

概率

概率的研究对象是样本空间

给定的参数确定了实验条件

固定参数得到不同实验结果对应不同的可能性叫做概率

以投掷硬币为例 H为正面 T 为反面

\[P(HTH;p = \theta) = \theta^2(1-\theta) \]

概率是概率空间向 [0,1]的一个映射

似然

似然的研究对象是参数空间

固定某个样本，似然函数是不同参数对应的可能性

但是一般来说，参数是客观存在的，是一个常量（上帝视角），并不是变量（不过未可知）

所以参数不具有密度函数

theta 的改变是人为的，于是叫做似然

比如掷硬币

有一个硬币，它有θ的概率会正面向上，有1-θ的概率反面向上。θ是存在的，但是你不知道它是多少。为了获得θ的值，你做了一个实验：将硬币抛10次，得到了一个正反序列：x=HHTTHTHHHH。

无论θ的值是多少，这个序列的概率值为 θ⋅θ⋅(1-θ)⋅(1-θ)⋅θ⋅(1-θ)⋅θ⋅θ⋅θ⋅θ = θ⁷ (1-θ)³

注意：不同的样本可能对应相同的概率值

比如，如果θ值为0，则得到这个序列的概率值为0。如果θ值为1/2，概率值为1/1024。

凭什么说 L(θ|x) = f(x;θ)

可以认为这就是似然函数的定义

似然函数不是参数的概率分布

\[L(\theta_m | x) = P(\theta_m | x) = \frac{P(\theta_m,x)}{P(x) = const} \\P(\theta_m,x) = P(x;\theta_m)P(\theta_m)\\ 后验 = 似然*先验 \]

似然函数和概率密度pdf的关系

似然是参数空间向[0,1]空间的一个映射

注意：似然函数根本上不具备概率的性质，只是一种普通的映射关系

Bayes formula

由来——公理化

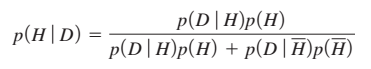
贝叶斯推断

样本分布(似然函数) + 先验概率

后验概率

最直观的理解：

Bayes 公式对发生了的现象根据证据发生的概率做了归一化

同样的一个事件，通常来说

P(H,D) hypothesis / data

\[P(综合推断) = \frac{P(正常情况)}{P(正常情况)+P(其他情况)} \]

贝叶斯估计当中参数先验分布的作用

不同的先验分布假设将会带来不同的后验推断结果

机器学习当中的 MLE，MAP，BaBesian

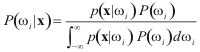
如何使用贝叶斯方法估计参数——使用似然函数

\[P(\theta|D) = \frac{P(\theta,D)}{P(D)[\text {same for all the data}]}\\P(\theta,D) = P(D|\theta)\pi{(\theta)}\\ \theta^* = argmax(P(\theta,D))\\ [\text{the determinator is constant}] \]

When one uses likelihood to get point estimates of model parameters, it’s called maximum-likelihood estimation, or MLE. If one also takes the prior into account, then it’s maximum a posteriori estimation (MAP). MLE and MAP are the same if the prior is uniform.

---

🔑例题

Thinking, Fast and Slow

每次看到贝叶斯定理几乎都会有一些新的理解。它作为一个普适规律，很简洁地给出了先验到后验的方法论。
我比较喜欢右边的这种表达形式。有趣的是，先验在其中直接作为乘数；而我们的观测结果，即证据，仍然需要通过结合一个普遍基于经验的条件概率，构造贝叶斯乘数来发挥作用。

这道题目出自Thinking, Fast and Slow 第二部分第十六节，题目也很有趣，叫做“Causes Trump Statistics”，说的是人们通常忽略群体属性的现象

在一个城市当中，有小黄和小蓝两家出租车公司，小黄占比85%，小蓝占比15%
有一名目击者说自己看到了一辆出租车违章，违章车辆是蓝色的，但是他也说自己对于两种车型，都有20%的可能看错车的颜色
那么蓝色车辆违章的概率是多少?

Thinking, Fast and Slow

\[\\ \textbf{Bayesian Theorem | E: Evidence H: Hypothesis}\\ P(H|E) = \frac{P(H) P(E|H)}{P(E)} = P(H)\frac{P(E|H)}{P(E)} \]

\[P(BlueInvolved |BlueSeen ) = P(BlueInvolved) \frac{P(BlueSeen|BlueInvolved)}{P(BlueSeen)} \]

\[P(BlueInvolved) = 0.15 \ (\text{prior from experience, i.e. Base Rate })\\ \]

\[P(BlueSeen | BlueInvolved) \\= 0.8 \text{ (from the witness)}\\ \]

\[P(BlueSeen) \\= P(BlueInvolved)P(BlueSeen|BlueInvolved) + \\P(BlueInvolved^c)P(BlueSeen|BlueInvolved^c) \\ =P(BlueInvolved)P(BlueSeen|BlueInvolved) + \\P(YellowInvolved)P(BlueSeen|YellowInvolved) \\ = 0.15 *0.8 + 0.85 *0.2\\ = 0.29 \textbf{( Total Probability Rule)} \]

\[P = 0.15 (\text{Base Rate})\frac{0.8 \text{ (Prob. of H given E)}}{0.29(\text{Prob. of E})} \approx0.41 \]

Monty Hall Problem

The Monty Hall problem is a counter-intuitive statistics puzzle:

• There are 3 doors, behind which are two goats and a car.
• You pick a door (call it door A). You’re hoping for the car of course.
• Monty Hall, the game show host, examines the other doors (B & C) and opens one with a goat. (If both doors have goats, he picks randomly.)

Here’s the game: Do you stick with door A (original guess) or switch to the unopened door? Does it matter?

我先自己尝试一下😂

• 首先，三扇门A,B,C是等效的
• 不妨假设选择了A，不管A当中有没有车，B,C当中肯定会有一只山羊
• 不妨假设主持人开的门是C

现在需要计算的是

• 在主持人已经开了一扇门的条件下
• Stick with A, Switch to B的获奖概率

啊啊啊我先自己尝试区分一下联合概率和条件概率

可以肯定的是，样本空间缩小了（C已经可以不考虑了），应该是条件概率

\[P(A|Host) = \frac{P(A,Host)}{P(Host)} \\ \]

先验概率

\[P(A) = P(B) = P(C) = \frac{1}{3} \ ? \]

感觉这个假设这么别扭呢……

不妨假设主持人开的门是C

那 P(C) = 1/3对吗？

🤔

换一个假设：把自己选择的门称作 A’

那么有(avg表示自己的随机选择)

\[P(A') = \text{avg}(P(A),P(B),P(C))=\frac{1}{3} \]

接着，主持人选择了一扇门，标记为C’

\[P(Host_{C'}) =P(A')\times\frac{1}{2}+ P(B')\times1 + P(C')\times0 = \frac{1}{2}P(A')+ P(B') = \frac{3}{2} \cdot\frac{1}{3} = \frac{1}{2} \]

这里又出现一个很奇怪的问题了

\[P(B') \]

是个什么东西？？

感觉应该是

\[P(B'|Host_{C'})? \]

另外

既然是标记为C’，

那么P(Host_C’)应该等于1吧 😱

接下来考虑

\[P(A'|Host_{C'})\\ P(B'|Host_{C'}) \]

写不下去了……😂

\[P(A'|Host_{C'}) = \frac{P(A',Host_{C'})}{P(Host_{C'})} =\frac{P(A')\cdot P(Host_{C'}|A')}{\frac{1}{2}} = 2(\frac{1}{3}\cdot\frac{1}{2}) = \frac{1}{3} \]

\[P(B'|Host_{C'}) = \frac{P(B',Host_{C'})}{P(Host_{C'})} =\frac{P(B')\cdot P(Host_{C'}|B')}{\frac{1}{2}} = 2(\frac{1}{3}\cdot1) = \frac{2}{3} \]

换！

Switch

男孩女孩

• 一个家庭两个孩子
• 有一个孩子是女孩，求另一个孩子也是女孩子的概率

我的答案

\[P(girl_2|girl_1) = P(girl_2) = \frac{1}{2} \]

李永乐老师的解答

至少一个是女孩 P = 1/3

第一个是女孩 P = 1/2

三囚犯问题

• ABC三个死囚，某人被赦免
• 看守可以告诉他将被杀死
• A的提问是否会让自己被赦免的概率提高？

我的答案

不可能，P(A) = 1/3

因为看守无法在客观上决定赦免的结果，因此，即使是选择性地提供信息，也是无效的

这也的确是答案

但是问题是

为什么一个提问，会让C被赦免的概率提高呢？

并不
C被赦免的概率永远是1/3，实际提高的概率是在看守说出某个死囚情况之后，另一个人被赦免的条件概率
独立事件，条件概率大于联合概率

条件概率的实质是改变了样本空间

ref

1. [PDF]The Bayesian Approach to the Philosophy of Science

2. [PDF] Maximum Likelihood vs. Bayesian Parameter Estimation

3. Can a posterior probability be >1?

4. [PDF]Chapter 12 Bayesian Inference - CMU Statistics