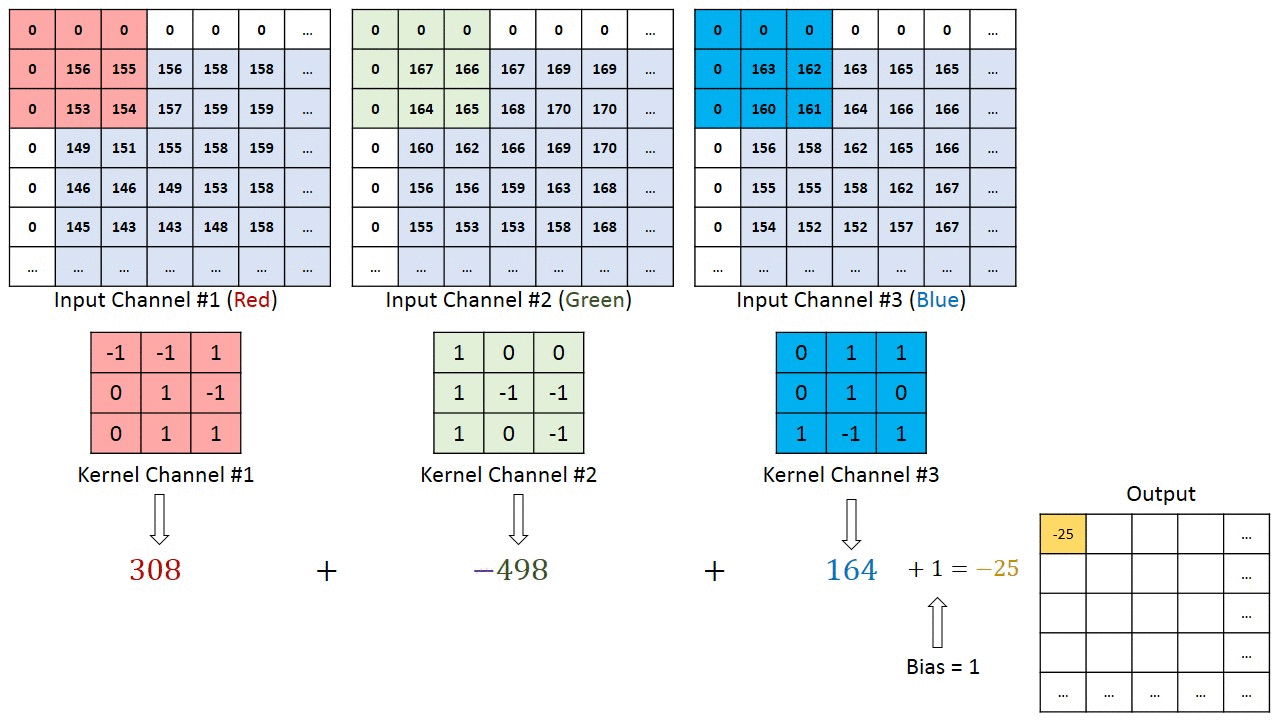
卷积和滤波器的关系 / 为什么2D卷积的卷积单元是3D的

Filters and Convolutions

Excerpt from Focal Loss

Classification Subnet:

The classification subnet predicts the probability of object presence at each spatial position for each of the A anchors and K object classes. This subnet is a small FCN attached to each FPN level; parameters of this subnet are shared across all pyramid levels.

Its design is simple. Taking an input feature map with \(C\) channels from a given pyramid level, the subnet applies four \(3\times 3\) conv layers, each with \(C\) filters and each followed by ReLU activations, followed by a \(3\times 3\) conv layer with \(K\times A\) filters. Finally sigmoid activations are attached to output the \(K\times A\) binary predictions per spatial location, see Figure 5 (c).

We use \(C\) = 256 and A = 9 in most experiments. In contrast to RPN [3], our object classification subnet is deeper, uses only \(3\times 3\) convs, and does not share parameters with the box regression subnet (described next).We found these higherlevel design decisions to be more important than specific values of hyperparameters.

Filters and Convs

\(\mathcal{C}\) 2D filters of size \(h\times w\) can be concatenated to form one 3D filter of size \(\mathcal{C} \times h \times w\)

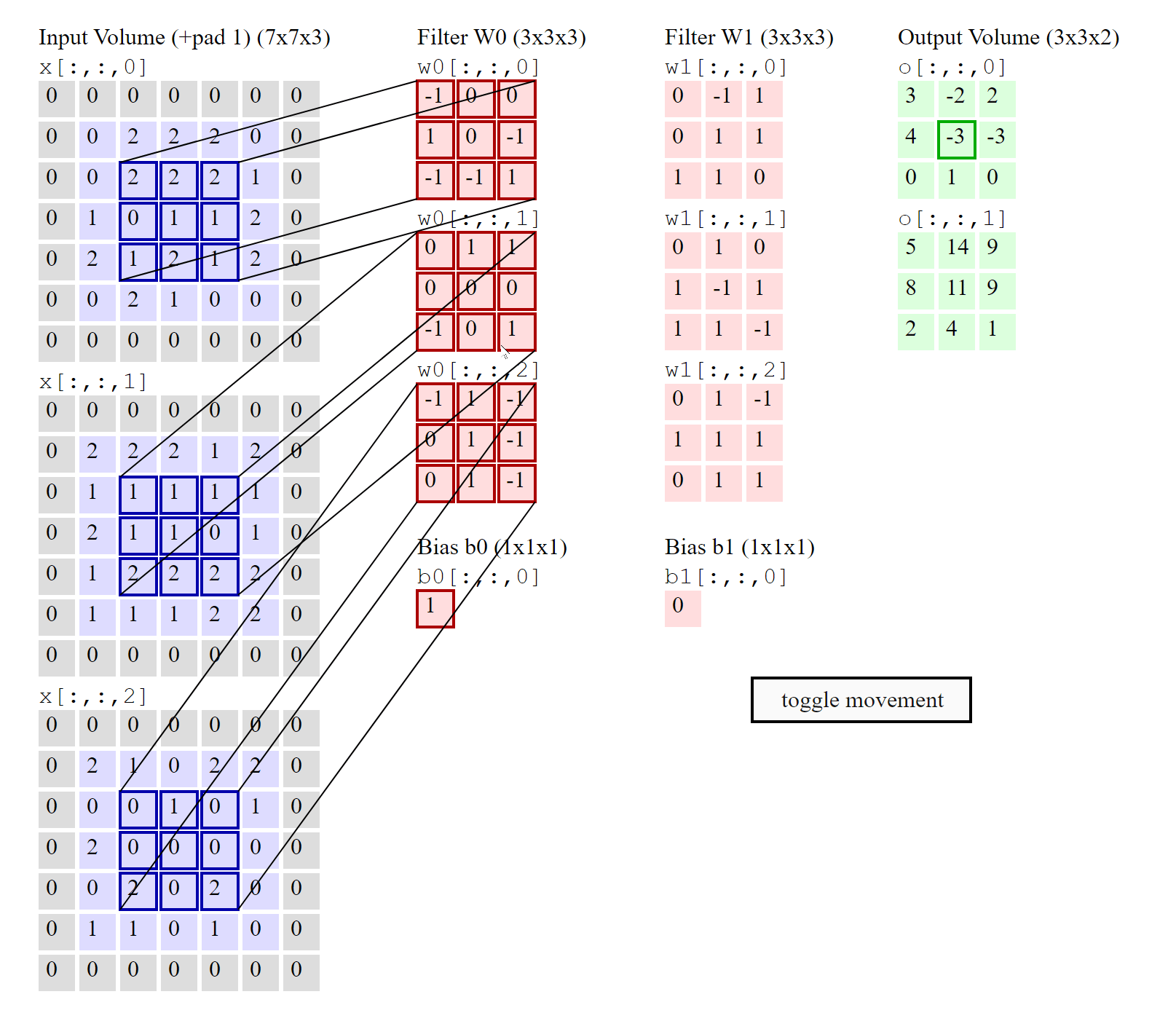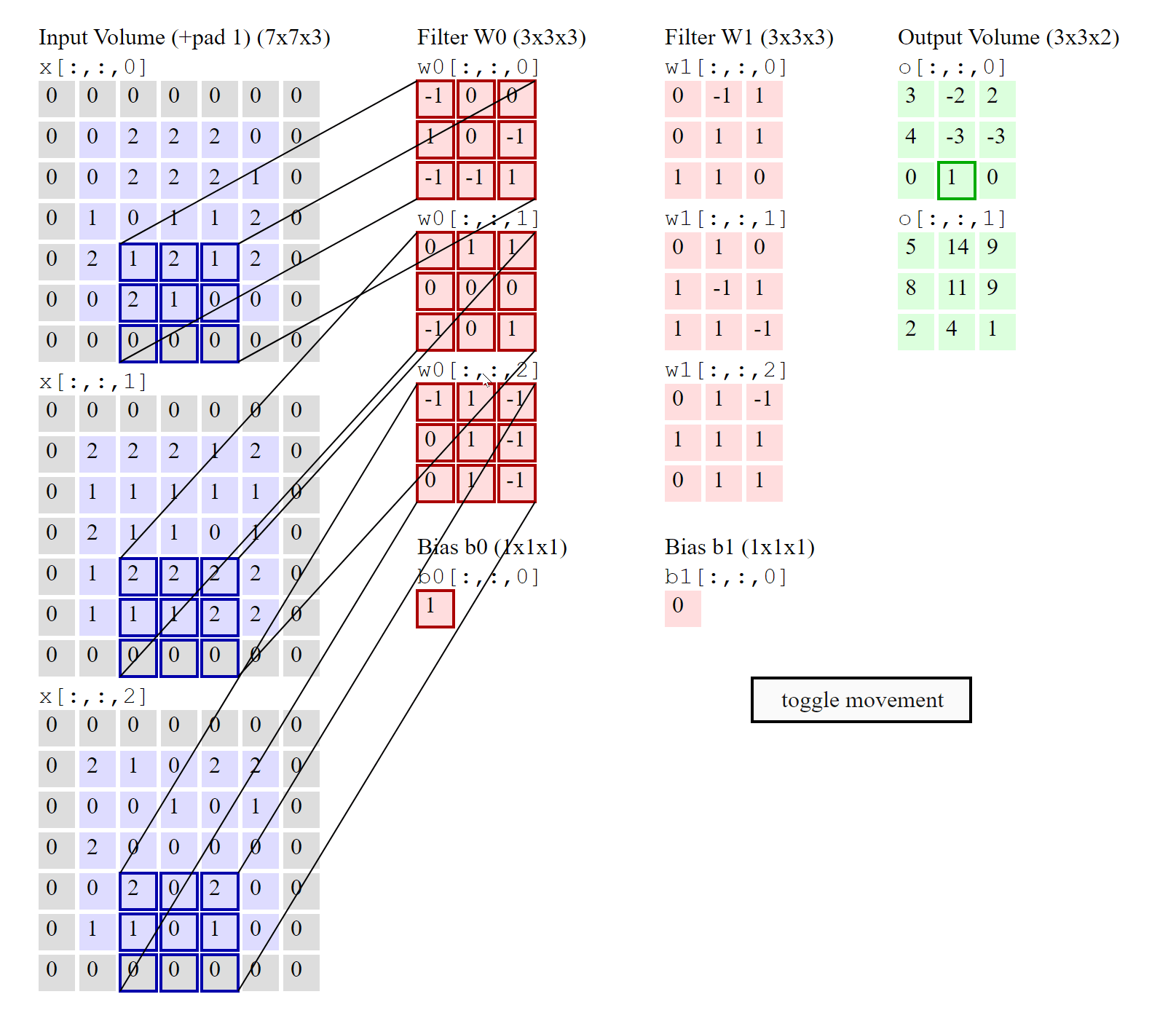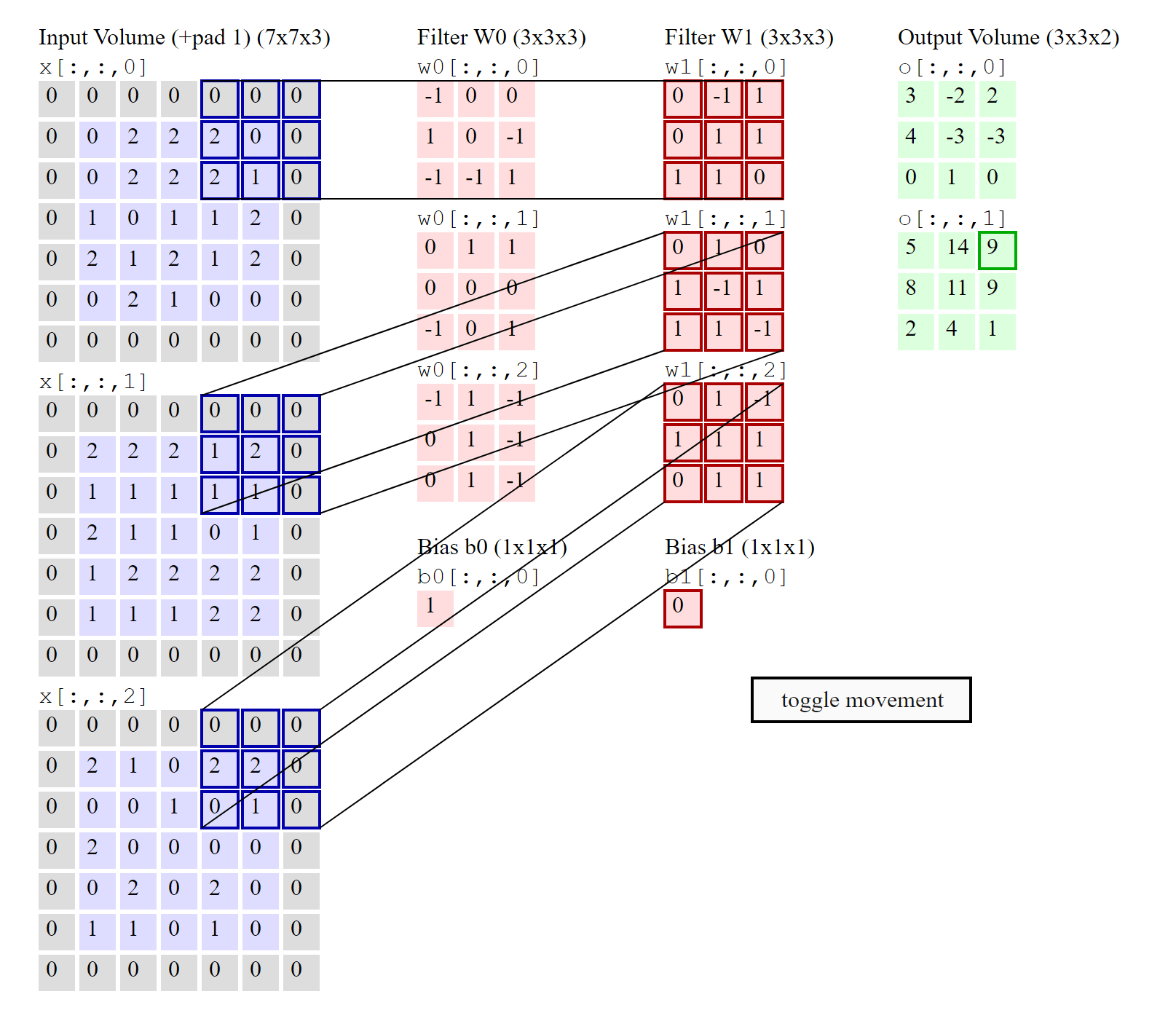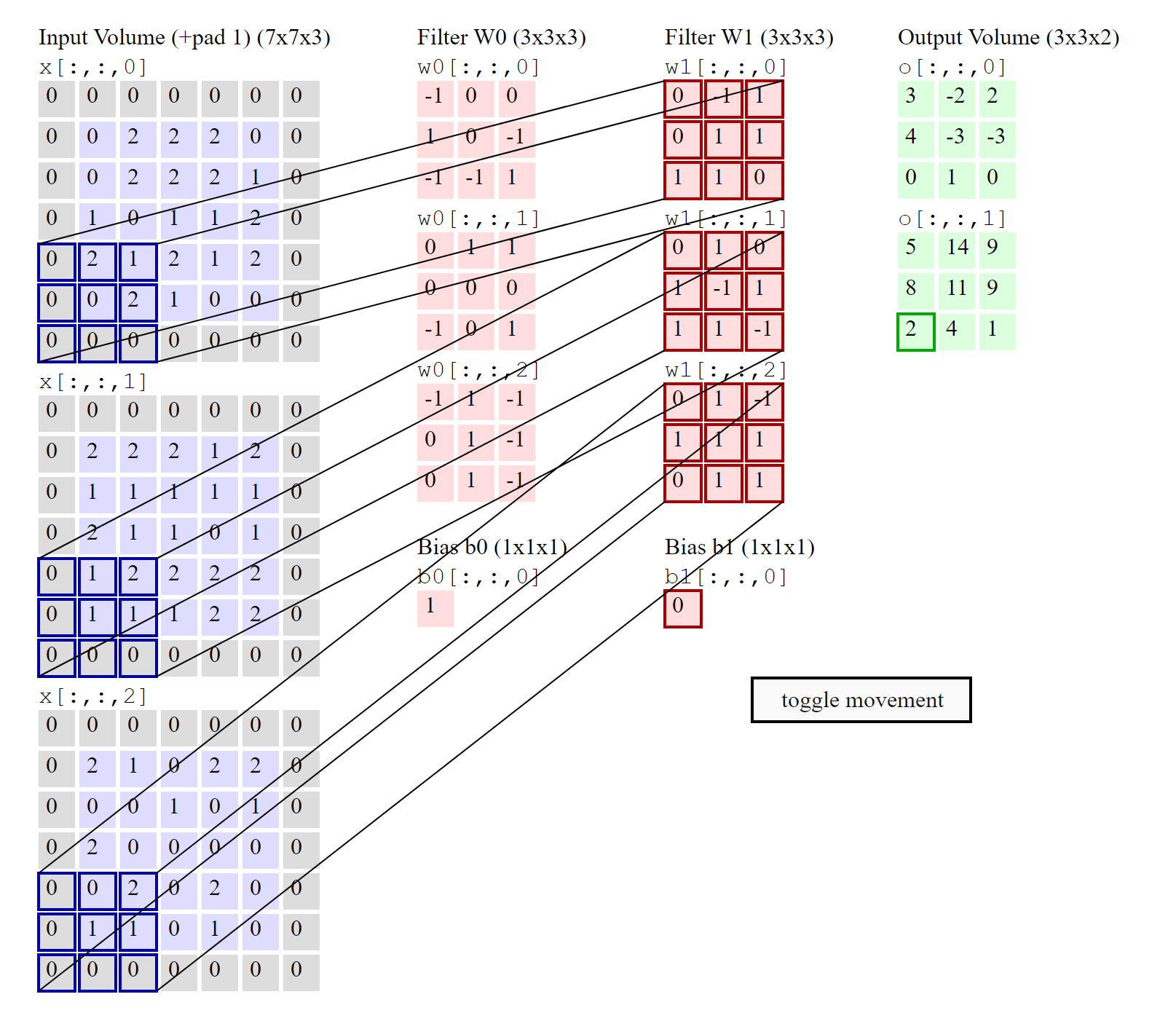
如果我说 3x3 conv，并且输入图像有\(\mathcal{C}_{in}\)个维度，希望网络的输出有\(\mathcal{C}_{out}\)个通道，那么

• 总共需要有\(\mathcal{C}_{out}\)个\(3\times 3\)卷积单元
• 每个卷积单元有\(\mathcal{C}_{in}\)个滤波器
• \(\mathcal{C}_{in}\)个滤波器滤波器大小均为\(3\times 3\)，在\(\mathcal{C}_{in}\)个输入通道上单独运作

• 每个2D卷积单元实际上是一个\(\mathcal{C}_{in} \times 3\times 3\) 的3D权重矩阵

叫2D的原因是卷积核步长移动的维度是2D的

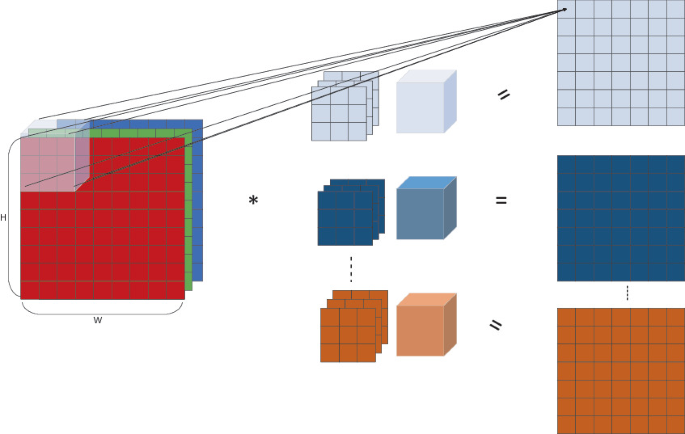
So, is there a separate filter for each input channel?

ref: https://ai.stackexchange.com/questions/5769/in-a-cnn-does-each-new-filter-have-different-weights-for-each-input-channel-or

YES, there are as many 2D filters as the number of input channels in the image. However, it helps if you think that for input matrices with more than one channel, there is only one 3D filter (as shown in the image above).

Then why is this called 2D convolution (if the filter is 3D and the input matrix is 3D)?

This is 2D convolution because the strides of the filter are along the height and width dimensions only (NOT depth) and therefore, the output produced by this convolution is also a 2D matrix. The number of movement directions of the filter determines the dimensions of convolution.

Note: If you build up your understanding by visualizing a single 3D filter instead of multiple 2D filters (one for each layer), then you will have an easy time understanding advanced CNN architectures like Resnet, InceptionV3, etc.