信息论基础概念、定理（二）

微分熵

微分熵\(H(f)\)可以为负

正态分布的微分熵\(\frac{1}{2}\log (2\pi e \sigma^{2})\)

连续AEP

熵的几何意义：

代表典型随机变量序列分布的边长的对数值*n

实际上是刻画典型集规模的物理量

微分熵和离散熵之间的关系

\[H(X^{\Delta}) \to h(f) - \log \Delta \]

如果采用二进制比特n位量化处理(\(\Delta = 2^{-n}\))，则有

\[H(X^{\Delta}) \to h(f) + n \]

在精确到n位的意义下，\(h(f)\)是为了描述\(X =f(x)\)所需要的平均比特数，即\(H(X^{\Delta})\)。

联合微分熵,条件微分熵,相对熵,互信息

联合微分熵

\[-\int_{\mathbf{x}} f(\mathbf{x})\log f(\mathbf{x})\text{d}\mathbf{x} \]

\(\mathbf{x} = X^{n}\)

多元正态分布的熵\(\frac{1}{2}\log[(2\pi e)^{n}|K|])\)

条件微分熵

\[-\int_{\mathcal{X},\mathcal{Y}}f(x,y)\log f(x|y)\text{d}x\text{d}y \]

相对熵

\(D(f||g) = -\int f \log \frac{f}{g}\)

互信息

\[I(X;Y) = \int f(x,y)\log \frac{f(x,y)}{f(x)f(y)} = D(\{X,Y\}||\{XY\}) \]

性质

\(D(f||g)\geq 0\)
- 当且仅当f=g几乎处处成立
\(I(f;g)\geq 0\)
\(h(X|Y) \leq h(X)\)
- 当且仅当f,g相互独立时成立？
- 多元正态分布，独立性
\(h(X_{1},\cdots,X_{n})\leq \sum_{i}^{n}h(X)\)
- 当且仅当相互独立时等号成立

Hadamard 不等式

\[|K|\leq \prod_{i}^{n}K_{ii} \]
联合熵<熵的乘积

微分熵的运算性质

\(h(X+c) = h(X)\)
\(h(aX) = h(X) + \log|a|\)
- \(h(\mathbf{A}X) = h(X) + \log|\text{det}(\mathbf{A})|\)
联合熵的链式法则

二阶矩最大熵

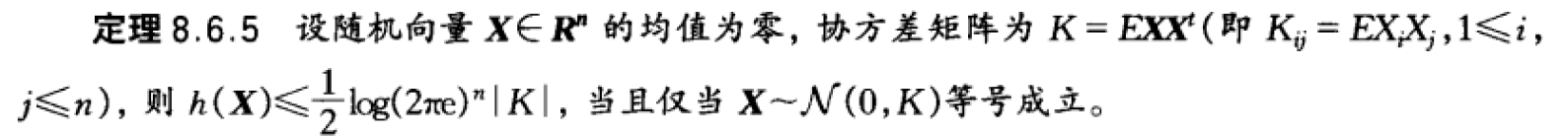
最小二乘误差与微分熵

\[E(X-\hat{X}) \geq \frac{1}{2\pi e}e^{2h(X)} \]

\[E(X-\hat{X}(Y)) \geq \frac{1}{2\pi e}e^{2h(X|Y)} \]

推论

常见的最大熵推导

高斯信道

最重要的连续字母表信道

概念

\(Y_{t} = X_{t} + Z_{t}, Z_{t} \sim \mathcal{N}(0,N)\),与输入信号相互独立

平均功率

高斯信道与离散信道

高斯信道可以直觉地转化成为离散信道

有功率限制的高斯信道容量
平均码长与可达性

信道容量

在\(E(X^{2})\leq P,Z\sim \mathcal{N}(0,N)\)的前提下

\[C = \frac{1}{2}\log(1+\frac{P}{N}) \]

最大值在\(X\sim \mathcal{N}(0,P)\)时达到

高斯信道编码定理

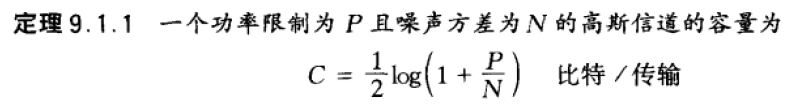
高斯信道编码定理的逆定理

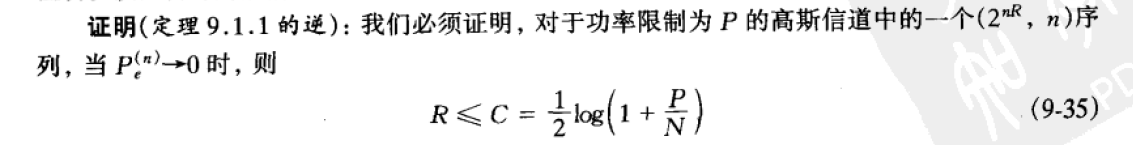
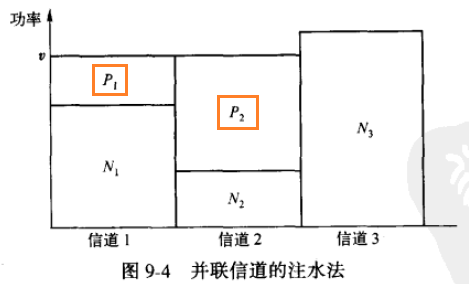
并联高斯信道

\[\sum_{i}P_{i} = P \]

率失真理论

概念

首先讨论离散情况

失真函数 \(d:\mathcal{X} \times \hat{\mathcal{X}} \to R^{+}\)
- 汉明失真/误差概率失真
- MSE失真
序列失真
- \(\frac{1}{n}\sum_{i}d(x,\hat{x})\)

率失真码和率失真函数

\((2^{nR},n)\)，对于序列的率失真码

序列编码函数\(f\)
- 分配区域
序列译码函数\(g: \{i\} \to \hat{\mathcal{X}}^{n}\)
- 码簿
序列失真\(D = Ed\)

率失真区域

率失真函数 \(R(D)\)

失真率函数 \(D(R)\)（不常用）

信息率失真函数

率失真定理

信息率失真函数和率失真函数等价

率失真定理

\[R(D) = R^{(I)}(D) \]

率失真函数的计算

伯努利

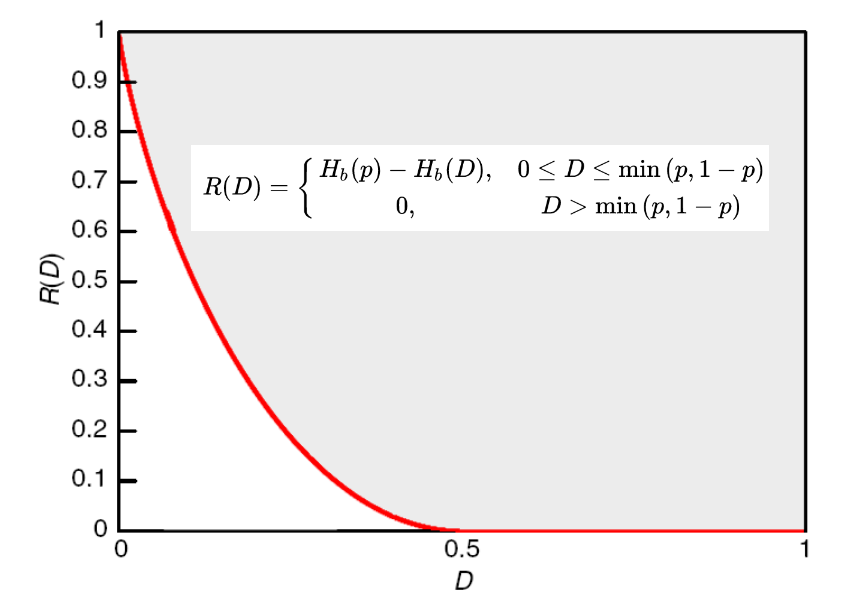
高斯

\(R(D) = \frac{1}{2}\log\frac{\sigma^{2}}{D}\)

\(D(R) = R^{-1}(D)\)

并联高斯信源的率失真

????

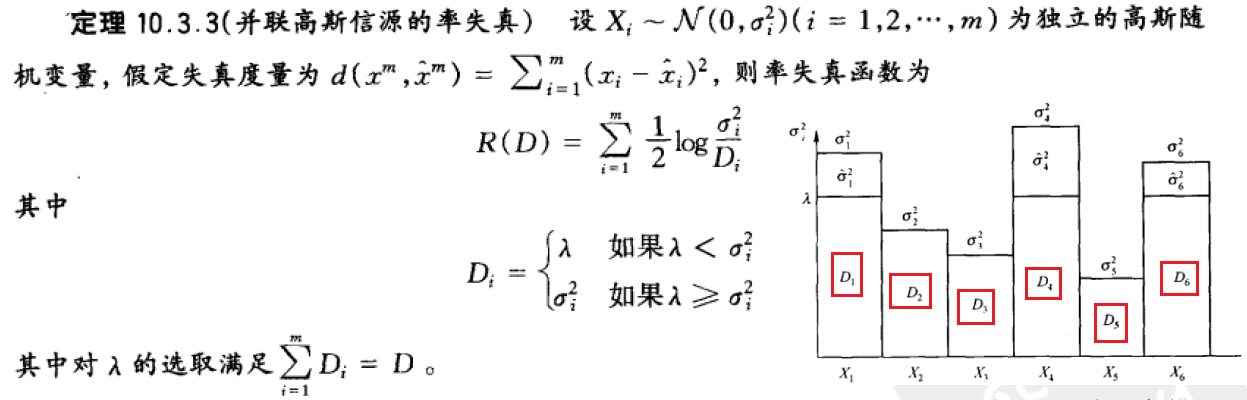
率失真定理的逆定理

率失真函数的可达性

失真典型集\(\subset\)联合典型集

其他？？

信息论与统计学

概念

概率单纯形

\(\mathcal{X} = \{1,2,3\}\)
\(\mathbf{x} = 11231\)
型 \(P\)指一种概率分布
- 比如\(x\sim \text{B}(7,0.3)\)，\(\mathbf{x} = \red{11}00\red{1}0\red{1}\)就属于一个型。\((\texttt{1} \times 4,\texttt{0} \times 3)\)
- 比如\((3P_{1},2P_{2},5P_{3})\)，代表个数为\(n = 3+2+5 = 10\)的序列，字母表规模为\(3\)的一类序列
序列的型 \(P_{\mathbf{x}} = \{P_{\mathbf{x}}(1) = \frac{3}{5},P_{\mathbf{x}}(2) = \frac{1}{5},P_{\mathbf{x}}(3) = \frac{1}{5}\}\)
- \(P_{\mathbf{x}}(k) = \text{Pr}\{x = k:x\in \mathbf{x}\}\)
- \(P_{\mathbf{x}}\)是一个\(\mathcal{X}\)上的概率分布
型的型类 (type class) \(T(P_{\mathbf{x}})\)
- 所有含有3个1，1个2，1个3的序列
\(\mathcal{P}_{n}\) 表示字母表上所有可能的型的集合
- 若 \(\mathcal{X} = \{a,b\}\)

\[\mathcal{P}_{3} = \{(N_{a} = 0,N_{b} = 3),(N_{a} = 1,N_{b} =2),(N_{a} = 3,N_{b} = 0)\} \]

\(Q^{n}(\mathbf{x}) = P(X^{n} = \mathbf{x})\)
- 其中\(X^{n}\)表示由一个确定的随机变量分布\(Q(X_{i})\)生成的，n个时间步的序列
\(Q^{n}(T(P_{\mathbf{x}})) = \sum_{\mathbf{x} \in T(P_{\mathbf{x}})}Q^{n}(\mathbf{x})\)

注意：型类中的序列概率均相等，因此有

\[Q^{n}(\mathbf{x}) \cdot |T(P_{\mathbf{x}})| = Q^{n}(T(P_{\mathbf{x}})) \]

型的基本定理

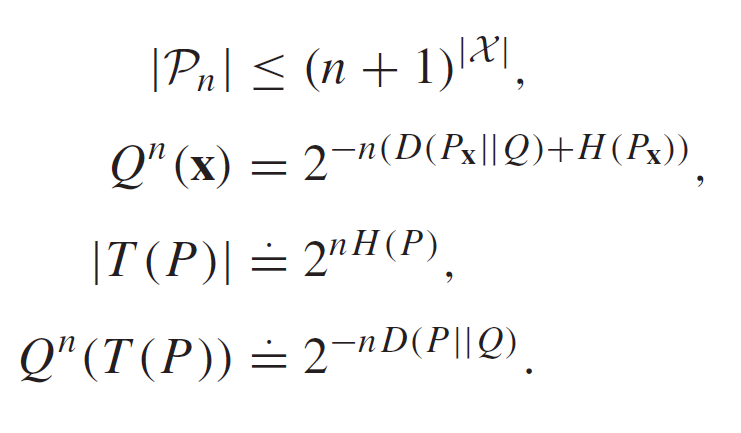
型的种类：多项式规模

型类中型的个数：指数规模

一个有用的估计

\[\binom{n}{k} \simeq 2^{nH(\frac{k}{n})} \]

每一个n维序列的型向量

\[\{\frac{n_{1}}{n},\frac{n_{2}}{n},\cdots,\frac{n_{|\mathcal{X}|}}{n}\},\sum_{i}n_{i} = n \]

大数定律

型的最重要的性质是：型的数量仅为多项式级，而每个型的因可序列数重为指数级。

由于每个型类的概率以指数依赖于\(D(P||Q)\)，所以对于远离真实分布的型类的概率依指数衰减。

- Question: 什么是真实分布
+ Note: 真实分布就是序列单个元素之间的分布
+ 通常都假定序列的生成是一个iid随机过程

通用信源编码

- Question: 码率到底是个什么东西

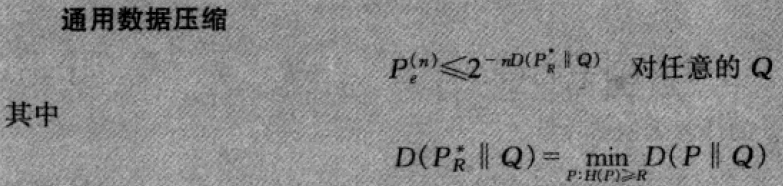
Sanov定理

估计由非典型序列的型构成的集合的概率

\(10010\)

\(n = 5\)
\(P_{\mathbf{x}}(1) = \frac{2}{5},P_{\mathbf{x}}(0) = \frac{3}{5}\)

两种描述

\(\frac{1}{5}\sum_{i= 1}^{5}g(x_{i})\geq \alpha\)
- 对于10010这个序列就是
- \(\frac{1}{5}[2g(1) + 3g(0)]\)
\(P_{\mathbf{x}}(1)g(1) + P_{\mathbf{x}}(2)g(2) \geq \alpha\)
- 对于10010这个序列就是
- \(\frac{2}{5}g(1) + \frac{3}{5}g(0)\)

意思就是：样本均值这件事情可以用型可进行表示，从\(\sum_{i}\)到\(\sum_{\mathcal{X}}\)

计算均值大于等于什么

例题

条件极限定理

相对熵的L1界

\[D(P_{1}||P_{2}) \geq \frac{1}{2\ln 2}||P_{1} - P_{2}||_{1}^{2} \]

条件极限定理

假设检验

TODO

费希尔信息与Cramer-Rao 不等式